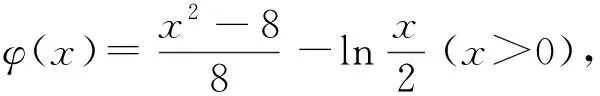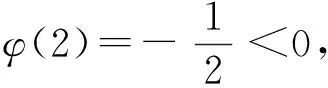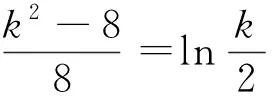两函数公切线问题
云南省玉溪第一中学 武增明 (邮编:653100)
函数图象的切线问题,一直是高考重点考查的内容,两个函数图象的公切线问题,内涵丰富,是高考命题的一个新热点.这两类问题求解数学思想是一致的,主要是化归与转化思想、函数与方程思想、数形结合思想.求解方法也是一致的,主要是:设出切点,利用切点处的导数即为切线的斜率,利用切点在切线上和曲线上联立方程组求解.但是,两个函数图象的公切线问题要比一个函数图象的切线问题复杂得多,灵活得多,难度大得多.下面笔者通过具体实例,归纳、总结两函数图象的公切线问题的类型及求解思想方法.
设曲线C1:y=f(x)在点A(x1,f(x1))处的切线为l1:y-f(x1)=f′(x1)(x-x1),整理得y=f′(x1)·x-f′(x1)·x1+f(x1).设曲线C2:y=g(x)在点B(x2,g(x2))处的切线为l2:y-g(x2)=g′(x2)(x-x2),整理可得y=g′(x2)·x-g′(x2)·x2+g(x2).由于l1与l2是相同的直线,故有
从而可以求出公切线方程.
从上述分析我们还可以看出,曲线C1:y=f(x)与曲线C2:y=g(x)公切线的条数等于该方程组解的个数.
1 求公切线方程



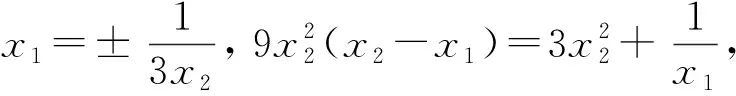
由两函数的图象知,x1与x2同号,即x1x2>0,


所以k=9,切点为(1,3),
所以两函数的方切线方程为
y-3=9(x-1),即9x-y-6=0.
例2 曲线x2=ky与曲线y=lnx的公切线方程为__________.




此题若用上述例1的解法,行不通!
2 求公切线方程中参数的值
例3 (2016年高考数学全国卷Ⅱ·理16)若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b=______.
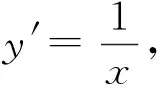


故直线y=kx+b为y=2x+1-ln2,所以b=1-ln2.
3 求函数中参数的值
例4 已知曲线y=x2-lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1也相切,则a=______.
解 因为曲线y=x2-lnx在点(1,1)处的切线的斜率为1,所以曲线y=x2-lnx在点(1,1)处的切线方程为y=x.
因为y=x与曲线y=ax2+(a+2)x+1相切,所以方程ax2+(a+2)x+1=x有一个实数根,即ax2+(a+1)x+1=0有唯一解,故△=0,即(a+1)2-4a=0,解得a=1.



4 求函数中参数的取值范围
例6 若曲线C1:y=x2与曲线C2:y=aex(a>0)存在公共切线,则a的取值范围是______.

例7 已知曲线y=ex+a与y=(x-1)2恰好存在两条公切线,则实数a的取值范围是( )
A.(-∞,2ln2+3) B.(-∞,2ln2-3)
C.(2ln2-3,+∞) D.(2ln2+3,+∞)
解y=ex+a的导数是y′=ex+a,
y=(x-1)2的导数是y′=2(x-1).
设两条曲线的公切线与曲线y=ex+a相切的切点为(m,n),则n=em+a,与曲线y=(x-1)2相切的切点为(s,t),则t=(s-1)2.
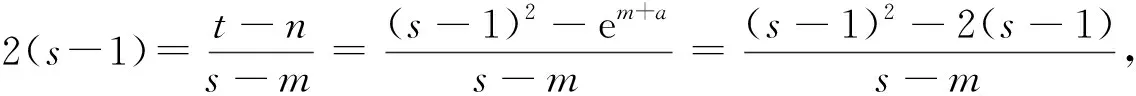
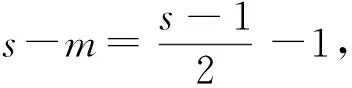
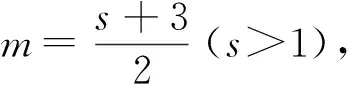


由f′(s)<0,得s>3,由f′(s)>0,得1 所以f(s)在s=3处取到最大值f(3)=2ln2-3. 所以a<2ln2-3,即a的取值范围是(-∞,2ln2-3).故选B. 评注 解答此类问题的思路是,从切线重合(即同一条切线)得到两切点的关系,转化所求变量与其中一个切点变量的函数关系,运用化归与转化思想、函数与方程思想,构造函数,并注意函数自变量的范围,通过求导确定函数单调性,运用数形结合思想,得到函数值域也即所求参数的取值范围. 解f′(x)=2x+2(1-a),设公切线与f(x)相切于点A(m,m2+2(1-a)m-4a),则切线方程为y-2+2(1-a)m-4a〗=m+2(1-a)〗(x-m),整理得y=m+2(1-a)〗x-m2-4a. 图1 例10 已知函数f(x)=ex,g(x)=lnx是否存在直线l,使得l同时是函数f(x),g(x)的切线?说明理由. 令h(m)=em(1-m)+m+1, 因为h(1)=2>0,h(2)=-e2+3<0,所以方程em(1-m)+m+1=0有解,则方程组有解,故存在直线同时是函数f(x)和g(x)的切线. (1)求f(x)的极大值; 解 (1)略. 假设函数F(x),g(x)的图象在其公共点(x0,y0)处存在公切线, 又函数的定义域为(0,+∞), 所以函数F(x)与g(x)的图象在其公共点处不存在公切线. φ(x)在(0,2)内递减,(2,+∞)内递增, 且当x→0时,φ(x)→+∞;当x→+∞时,φ(x)→+∞. 所以φ(x)在(0,+∞)内有两个零点, 综上,当k≤0时,函数F(x)与g(x)的图象在其公共点处不存在公切线;当k>0时,符合题意的k的值有2个.
5 求切点横坐标的取值范围



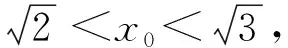
6 判断公切线的条数
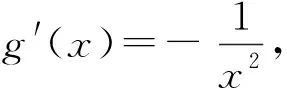
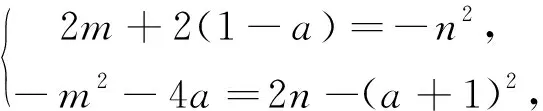
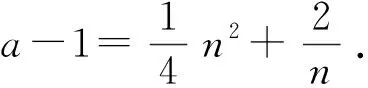


7 探究是否存在公切线