对2018年高考数学全国卷Ⅰ第16题的赏析

新疆乌鲁木齐市第八中学 李昌成 车燕昭 (邮编：830002)

普通高中数学课程标准要求：高中数学课程应注意提高学生的数学思维能力，这是数学教育的基本目标之一……数学思维能力在形成理性思维中发挥着独特的作用.

考试大纲指出：高考对能力的考查，强调“以能力立意”，就是以数学知识为载体，从问题入手，把握学科的整体意义，用统一的数学观点组织材料.

现在的高考题正在积极落实新课标和考试大纲精神，每年都会命制一些凸显能力立意的试题，增加试卷的区分度，以选拔优秀人才.2018年高考数学全国卷Ⅰ第16题就是一个典型例子.

1 试题呈现

题目 已知函数f(x)=2sinx+sin2x，则f(x)的最小值是______.

2 分析解答

解法1f′(x)=2cosx+2cos2x，由f′(x)=0，得2cos2x+cosx-1=0，解得

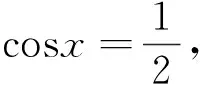
解法2 由于y=2sinx的最小正周期为2π，y=sin2x的最小正周期为π，由最小公倍数法知，f(x)的最小正周期为2π.下面给出证明：

f(x+2π)=2sin(x+2π)+sin2(x+2π)=2sinx+sin(2x+4π)=2sinx+sin2x=f(x)，所以本函数的最小正周期为T=2π.

所以T为f(x)+h(x)的一个周期.可以类似证明差、积、商情形.

下面在(0，2π)内研究本函数：

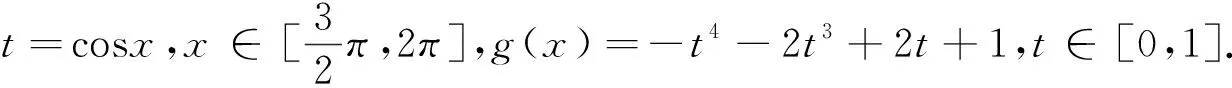
分析3 本题基本背景是三角函数，那么对于角的处理极为重要.本题中可以考虑用同角三角函数的平方关系，二倍角，扩角降幂等知识处理函数，从解法2可以发现最后的函数形式还是稍微有些复杂.我们可以再做角的文章，以期简化函数，方便解答.

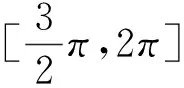
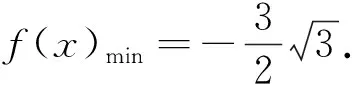
评注 从以上解法探究可以发现，本题以三角函数为背景，应用导数，综合考查了三角和导数的知识和技能，对学生的能力要求还是较高的.学生若死盯着三角函数，仅依靠三角函数的知识、方法，甚至是技巧都是无济于事的.这正是本题命题意图，希望学生有扎实的功底，严谨的推理，缜密的思维等能力.对于靠刷题应对高考的学生而言，此题显得举步维艰.本题若变形成：“已知函数f(x)=2sinxsin2x，则f(x)的最小值是____.”学生感觉就会舒坦多了，因为这两题具有异曲同工之妙.但是，能力就体现在创新之中.

3 立意分析

能力立意的高考命题，强调向能力测量转变，考查学生继续学习的潜能，本题在能力立意方面非同一般，在亲切平和中默默绽放.

应用意识和创新意识强烈.学生猛然一看，并不可怕，题面就是再常见不过的三角函数，经过命题专家精心处理，题目脱去老套和俗气.学生就三角论三角没有出路，必须开拓思路，借助导数或基本不等式强大功能，方可推进解答.这是一种创新，也是一种应用，更是能力提升，知识融合.

逻辑思维能力凸显.从三角函数入手，抽丝剥茧，周期性缩小思考面；数形结合引导分类讨论；三角公式的选择构造不同的函数；导数最终完美收官；奇偶性的巧妙应用；多项均值不等式的构造.这一系列动作的主线就是逻辑思维的考查.

运算能力贯穿其中.无论哪一种办法均离不开对应的运算，本题有三角运算，指数运算等诸多运算，每一步若出错都不会露出任何蛛丝马迹，最终让学生劳而无功.尤其是最值部分的运算，要么次数较高，要么夹杂概念，都是对学生的运算考验.

4 结束语

数学教学不仅要教会学生基本的技能技巧，更要在培养能力上下工夫，切勿让题海战术耽误了学生的青春时光.思维的训练，能力的培养都是数学核心素养形成的必经之路.