非均匀噪声背景下信源数估计算法

陈明建 龙国庆 黄中瑞

(国防科技大学电子对抗学院,安徽合肥 230037)

1 引言

阵列信号空间谱估计在雷达、声纳、移动通信以及语音增强等领域研究有着广泛的应用[1-2]。特别是基于子空间的多信号分类法(MUSIC)[3-5]、旋转子空间不变法(ESPRIT)[5]以及子空间拟合法[6]。子空间类的DOA估计算法应用前提是信源数准确已知。因此信源数目估计是基于子空间类超分辨DOA估计算法首要解决的问题。

典型的信源数估计方法主要包括：基于AIC准则[7]和MDL准则[8-10]的信息论方法、基于特征值一步预测法[11]、贝叶斯预测密度法[12]等。这些方法应用的前提是假定阵元噪声为高斯白噪声,而实际的噪声模型可能是空间非平稳,非均匀噪声。近些年来,学者们相继提出了色噪声背景下的信源数估计方法,如盖氏圆盘法(GDE)[13]、正则相关法[14]、基于对角加载的特征值校正方法[15]等。GDE法同时利用了特征值和特征向量信息,因此在色噪声条件下仍然可以正确估计信源数,但在低信噪比时性能较差,且需要人工选择调整因子。正则相关法对阵列几何结构是严格限制,因此实用性受到了极大的限制。基于对角加载的信源数估计方法一定程度上解决噪声特征值发散引起信源数估计性能下降的问题,但是需要人为设置对角加载量,最优加载量无法准确获得。

针对非均匀噪声背景下信源数估计问题,本文提出基于修正数据协方差矩阵的SORTE信源数估计方法。该方法首先通过构造特殊对角矩阵得到修正的数据协方差矩阵。该矩阵包含了信源所有信息,并剔除了非均匀噪声影响；然后利用该矩阵对应特征值二阶统计量的方差信息,构造SORTE判决函数实现信源数估计。

2 信号模型

假设K个远场窄带信号以角度θ=[θ1,θ2,…,θK]T入射到M元均匀线阵上,符号(·)T表示转置。阵元间距为半波长；假定阵列噪声为时间平稳、空间非平稳的零均值复高斯噪声,则阵列接收信号可表示为

(1)

其中a(θ)是阵列导向矢量,表示为

a(θ)=[1,e-jsin θ,…,e-j(M-1)sin θ]T

(2)

A(θ)=[a(θ1),…,a(θK)]为导向矢量矩阵。s(t)=[s1(t),…,sK(t)]T为入射信号源矢量；n(t)非均匀噪声矢量。则x(t)的协方差矩阵可表示为

R=E{x(t)xH(t)}=ARsAH+Q

(3)

式中：为了行文的简洁,A(θ)简写为A。符号E{·}、(·)H分别表示统计期望值、共轭转置,Rs=E{s(t)sH(t)}、Q=E{n(t)nH(t)}。若噪声为空时均不相关的非均匀噪声,则Q可表示为

(4)

3 信源数估计方法

3.1 基于对角加载的MDL法

(5)

在理想白噪声背景下噪声特征值近似相等,MDL准则能有效实现信源数一致估计,但在空间非均匀噪声背景下噪声特征值发散,此时基于MDL准则估计方法将失效。针对该问题,基于对角加载的修正采样数据协方差矩阵可表示为

(6)

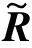
3.2 盖氏圆方法

盖氏圆方法是对R进行酉变换估计信源数。若对R进行分块

(7)

其中R′为R前M-1行和前M-1列组成的矩阵。利用R′特征分解得到特征向量矩阵V构造酉变换矩阵T

(8)

酉变换矩阵T对协方差矩阵R进行如下变换

(9)

则GDE准则可描述为

(10)

式中,D(N)是与快拍数有关的调整因子。当k由小到大进行取值时,假设当k=kGDE时,GDE(k)第一次出现负数,则信源数为kGDE-1。

3.3 本文方法

(1)修正的数据协方差矩阵

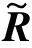
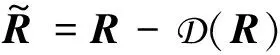
(11)

符号D(R)表示对角矩阵,其对角线元素为矩阵R的主对角线元素。式(11)可以等价表示为

(12)

(13)

证明假定A的第m行向量表示为bm[am(θ1),…,am(θK)],则ARsAH主对角线上的第m个元素表示为

(14)

式中：Pk为第k信源的功率,且利用了|am(θk)|=1的关系。

(15)

对ARsAH进行特征分解,可得

(16)

将式(16)代入到式(15)可得

(17)

(2)SORTE法信源估计

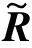
(18)

(19)

利用特征值方差信息构造判决函数为[17]

(20)

由式(18)、(19)、(20)可知

(21)

则可得信源估计的判决函数为

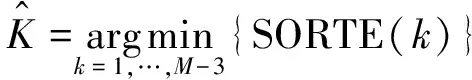
(22)

4 仿真实验与分析

实验1白噪声背景下正确检测概率与信噪比、快拍数关系

假定噪声为空时高斯白噪声。图1是快拍数为200时正确检测概率与SNR关系曲线。图2是SNR为0 dB时正确检测概率与快拍数关系曲线。

图1 白噪声背景下正确检测概率与SNR关系

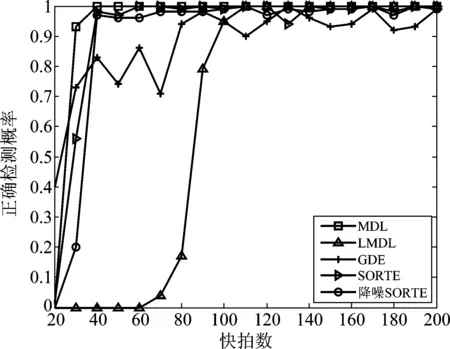
图2 白噪声背景下正确检测概率与快拍数关系

由图1可知,在高斯白噪声条件下,所有信源数估法在一定SNR条件下均能实现100%成功估计,但本文方法和SORTE法在低SNR条件性能更优,两者性能接近；MDL法性能次之,而基LMDL法在白噪声背景下反而性能更差。这是由于特征值校正是以牺牲SNR为代价,对角加载相当于向阵列注入白噪声。

由图2可知：当SNR为0 dB时GDE法在短快拍时正确检测概率达到了40%以上,但收敛速度较慢,由于GDE法调整参数D(N)与快拍数相关,若采用固定的调整参数,则在不同快拍数时算法性能稳定性较差；MDL法、SORTE法以及本文算法在短快拍时性能接近,收敛速度较快。LMDL法由于人为注入白噪声,等价于降低SNR,因此其性能最差。

实验2色噪声背景下正确检测概率与信噪比、快拍数关系

假设噪声为非均匀空间色噪声,图3为采样快拍数为200时正确检测概率与SNR的关系曲线。图4为SNR为0 dB时正确检测概率与快拍数的关系曲线。

图3 色噪声背景下正确检测概率与SNR关系

图4 色噪声背景下正确检测概率与快拍数关系

由图3可知,在非均匀噪声条件下,MDL算法失效,LMDL、GDE法在色噪声背景下均能实现信源数有效估计,但两种算法性能受限于算法调整参数,至今没有合适的准则选择最优的算法调整参数；SORTE法性能介于MDL与GDE之间,由于非均匀噪声的影响,其实现100%正确检测的信噪比门限大于4 dB,而本文算法在SNR大于-5 dB时即可实现100%正确检测,且在低信噪比时其正确检测性能最优。这主要是因为本文算法利用数据协方差矩阵与其对角元素构成的对角矩阵相减,消除了非均匀噪声的影响,改善了算法在低信噪比时性能。

从图4可以看出,在SNR等于0 dB时MDL算法在色噪声条件下性能急剧恶化,无法估计信源数。而SORTE法和GDE法正确检测概率较低,只有本文方法和LMDL法能够实现一致估计,但本文算法收敛速度要优于LMDL法,即本文方法在短快拍条件信源数估计性能更优。

实验3色噪声背景下算法正确检测概率与WNPR关系

图5 不同WNPR时正确检测概率

由图5可知,不同WNPR对GDE法、LMDL法以及SORTE法性能影响较大。MDL、GDE法基本失效,SORTE、LMDL算法的正确检测概率均随着WNPR增大逐渐降低。只有本文方法对WNPR变化不敏感,即使在低SNR、高WNPR时其正确检测概率接近1,因此本文方法在非均匀噪声背景下信源数估计具有稳健性。

5 结论

针对非均匀空间色噪声背景下的信源数估计问题,本文提出了基于修正协方差矩阵的SORTE信源数估计方法。该方法通过构造新的协方差矩阵,剔除了非均匀噪声影响,然后利用构造协方差矩阵对应特征值的方差信息实现信源数估计。仿真结果表明：该方法在非均匀噪声背景下能够实现信源数的一致估计,尤其是在低信噪比、短快拍条件下信源数估计性能要优于其他类方法。

[1] Krim H, Viberg M. Two decades of array signal processing research: the parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4):67-94.

[2] Tuncer T E, Friedlander B. Classical and modern direction-of-arrival estimation [M]. Elsevier, Burlington, MA,2009.

[3] Liu G, Chen H, Sun X, et al. Modified music algorithm for DOA estimation with nyström approximation[J]. IEEE Sensors Journal, 2016, 16(12):4673- 4674.

[4] Basikolo T, Arai H. Aprd-music algorithm DOA estimation for reactance based uniform circular array[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(10):4415- 4422.

[5] Chen F J, Kwong S, Kok C W. ESPRIT-like two-dimensional DOA estimation for coherent signals[J]. IEEE Transactions on Aerospace & Electronic Systems, 2010, 46(3):1477-1484.

[6] Zhang X, Li Y, Yang X, et al. Sub-array weighting un-music: a unified framework and optimal weighting strategy[J]. IEEE Signal Processing Letters, 2014, 21(7):871- 874.

[7] Lu Z, Zoubir A M. Generalized bayesian information criterion for source enumeration in array processing[J]. IEEE Transactions on Signal Processing, 2013, 61(6):1470-1480.

[8] 许佳奇, 王川川, 曾勇虎,等. 盖尔圆定理和最小描述长度准则相结合的信源数目估计方法研究[J]. 信号处理, 2017,33(3A):53-57.

Xu Jiaqi,Wang Chuanchuan,Zeng Yonghu.Research on source number estimation based on Geschgorin disk estimator theorem and minimum description length criterion[J].Journal of Signal Processing,2017,33(3A):53-57.(in Chinese)

[9] Huang L, Xiao Y, Liu K, et al. Bayesian information criterion for source enumeration in large-scale adaptive antenna array[J]. IEEE Transactions on Vehicular Technology, 2016,65(5):3018-3032.

[10]艾健健, 刘成城, 赵拥军. 利用随机矩阵理论的MDL信源数估计算法[J]. 信号处理, 2015,31(2):186-193.

Ai Jianjian,Liu Chengcheng,Zhao Yongjun.MDL algorithm for source enumeration using random matrix theory[J].Journal of Signal Processing,2015,31(2):186-193.(in Chinese)

[11]Han K, Nehorai A. Improved source number detection and direction estimation with nested arrays and ULAs using jackknifing[J]. IEEE Transactions on Signal Processing, 2013, 61(23):6118- 6128.

[12]Cho C M, Djuric P M. Detection and estimation of DOA's of signals via Bayesian predictive densities[J]. IEEE Transactions on Signal Processing, 1994, 42(11):3051-3060.

[13]Huang L, Long T, Wu S. Source enumeration for high-resolution array processing using improved Gerschgorin radii without eigendecomposition[J]. IEEE Transactions on Signal Processing, 2008, 56(12):5916-5925.

[14]Stoica P, Wong K M, Wu Q. On a nonparametric detection method for array signal processing in correlated noise fields[J]. IEEE Transactions on Signal Processing, 2008, 44(4):1030-1032.

[15]张杰, 廖桂生, 王珏. 对角加载对信号源数检测性能的改善[J].电子学报, 2004, 32(12):2094-2097.

Zhang Jie,Liao Guisheng,Wang Yu.Performance improvement of source number detection using diagonal loading[J]. Acta Electronica Sinica, 2004, 32(12): 2094-2097.(in Chinese)

[16]Liao B, Huang L, Guo C, et al. New approaches to direction of arrival estimation with sensor arrays in unknown nonuniform noise[J]. IEEE Sensors Journal, 2016, 16(99):8982- 8989.

[17]He Z, Cichocki A, Xie S, et al.Detecting the number of clusters in n-way probabilistic clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(11):2006-2021.