CNN与CSP相结合的脑电特征提取与识别方法研究
孔祥浩 马 琳 薄洪健 李海峰
(哈尔滨工业大学计算机科学与技术学院,黑龙江哈尔滨 150001)
1 引言
研究对脑电(Electroencephalograph, EEG)信号的快速精准的解析方法,高效地实现从复杂的EEG信号中提取有用的认知信息,实现对外部设备的控制是脑机接口(Brain Computer Interface, BCI)[1-3]领域的核心问题。但由于大脑活动的复杂性,认知状态下的EEG信号不是脑认知信号和干扰信号的简单叠加,而是非线性、时变信号。因此,获得高效低维 EEG特征是BCI可靠应用的重中之重。近几年,通过大脑皮层电位信息来实现人与外界沟通联系的BCI技术成为了该领域的一个研究热点。2011年美国教授贺斌实现了基于运动想象的EEG控制三维空间的直升飞机飞行[4]。2012年,美国男子扎克·沃特利用脑控义肢,通过想象成功攀登了103层的芝加哥威利斯大厦。2014年巴西世界杯开幕式上,一名高位截瘫少年身穿脑控外骨骼盔甲大脑想象开出世界杯第一球。在国内的研究中,清华大学的高上凯课题组是研究脑电波控制技术最早的团队之一,于2006展示了利用运动想象控制机器狗进行踢球的BCI系统[5- 6]。快速地从复杂的脑电信号中获取有用的认知信息,进而实现对外部设备的控制,需要更加高效的信息解析技术。
小波变换[7-9]、AR模型[10-12]、频带能量[13-15]、独立分量分析[16-17]和公共空间模式[18-19]等信号处理算法常常应用于EEG信号的特征提取中。公共空间模式(Common Spatial pattern,CSP)算法做为一种高效的空间滤波算法,能够在最大化第一类方差的同时最小化另一类方差,采用同时对角化协方差矩阵的方式,得到具有最大分辨能力的特征向量。因此CSP作为一种有效的空间特征提取方法被广泛采用。
1991年,Z.J.Koles首次提出了应用在EEG信号中的CSP方法[20]。1999年H.Ramoser等人使用CSP方法对运动想象领域的多导EEG信号进行特征提取,取得了较好结果,然而这种方法仅考虑空间信息,而忽略了时间信息[21]。2012年Wojciech Samek等人提出了一种将CSP正则化到固定子空间(sCSP)的方法,增加了分类精度,特别是对那些难以控制BCI的受试者[22]。2013年Mahnaz Arvaneh等人提出了一种KLCSP算法在最大化类均值差异的同时,通过基于KL散度的损失函数的测量最小化类内的差异,但此方法过于依赖数据[23]。CSP能够在脑电特征提取过程中特异性提取空间信息特征,因此可以对含有大量电极的多通道脑电信号进行分析,但同时,含有大量电极的脑电信号必然含有大量的冗余信息,经CSP处理后的特征矩阵包含大量的冗余信息,这些冗余信息会导致计算复杂性提高,降低处理算法的速度,也会导致信号的识别率降低。因此需要对特征进行二次筛选,从特征矩阵中选择具有更加代表性的特征,能够提高识别率并降低计算的复杂性。
卷积神经网络[24](Convolutional Neural Network,CNN)是近些年发展起来,并广受重视的一种高效识别方法,特别是在模式识别领域,得到了广泛的应用。CNN不仅具有传统神经网络的容错性强、自适应能力强和自学习能力强的优点,还能够隐式地从训练数据中对特征模式进行学习,从而有效提取特征。另外,CNN具有局部权值共享的特殊结构,更加接近于实际的生物神经网络,而权值共享地特性降低了网络的复杂程度,因此对于多维输入向量可以直接输入网络,有效降低了特征提取和分类过程中数据重建的复杂程度。而且,在对网络的学习行为进行分析时,CNN相比于多层前馈网络更容易找到起作用的神经元,更容易观察到数据在网络中的表现形式,进而对整个学习过程有更加深度地理解。
本文针对脑电信号分类识别中的特征优化和选择问题进行研究。本文采用CSP算法提取脑电信号特征,其特征选择直观可见,便于对特征选择方法进行验证。利用CNN的学习特性对EEG分类识别中提取的大量特征进行优选,并定义基于CNN权值矩阵特性的特征筛选准则,得到效能高的最优特征集。本文工作在BCI Competition IV数据集[25]上进行了实验,证明了本文方法的高效性。本方法具有普遍性,适用于各种情况下的特征选择问题。
本文后续章节安排如下:第二部分主要介绍公共空间模式(CSP)和卷积神经网络(CNN)的基本原理,第三部分是对CNN与CSP相结合的脑电特征提取方法的基本原理,第四部分是对本文提出的脑电特征提取方法进行进一步的实验及相应结果分析,第五部分为本文结论。
2 公共空间模式(CSP)与卷积神经网络(CNN)技术原理
2.1 CSP原理
公共空间模式(CSP)算法做为一种高效的空间滤波算法,CSP算法的目标是创建出一个最优的公共空间滤波器,能够最大化一类方差的同时最小化另一类方差,采用同时对角化两类任务协方差矩阵的方式,得到两种任务的最大分辨能力的特征向量。

图1 CSP特征提取方法过程示意图
CSP算法的过程如下:
(1)先将原始数据按照类别分段。
将原始数据按照类别进行分段。如两类样本数据D可分段为D1和D2,D1表示第一类样本数据,D2表示第二类样本数据。
(2)计算分段后的原始数据的协方差矩阵。则协方差矩阵的计算方式如下:
(1)
其中,DT为矩阵D的转置矩阵,trace(D)表示求矩阵D的迹。
使用C1表示第一类样本数据的空间协方差矩阵的期望,C2表示第二类样本的空间协方差矩阵的期望,Cc表示两类数据的空间协方差矩阵之和,则有:
Cc=C1+C2
(2)
上述的协方差矩阵可以通过平均多次实验结果的方式获得。
(3)对空间协方差矩阵进行正交白化变换并且同时对角化。
Cc作为两个协方差矩阵的和,是一个正定矩阵,因此可令:
(3)
其中Uc表示特征向量矩阵,Λc表示特征值的对角阵。Λc中的特征值是降序排列的,白化转换Uc后可以得到:
(4)
将矩阵P作用于C1和C2,可得到:
S1=PC1PT,S2=PC2PT
(5)
S1、S2具有公共特征向量,而且存在两个对角矩阵Λ1、Λ2和特征向量矩阵B,满足如下的条件:
S1=BΛ1BT
(6)
S2=BΛ2BT
(7)
Λ1+Λ2=I
(8)
其中I是单位阵。由此可见特征值λ1和λ2的和等于1。
(4)计算投影矩阵。
对于特征向量矩阵B,当一个类别S1有最大的特征值时,此时另一个类别S2有最小的特征值,因此可以利用矩阵B实现两类问题的分类,可以得到投影矩阵:
W=(BTP)T
(9)
(5)经过投影得到特征矩阵。
因此可以将一个原始脑电数据EM×N通过投影矩阵W进行投影,得到:
ZM×N=WM×MEM×N
(10)
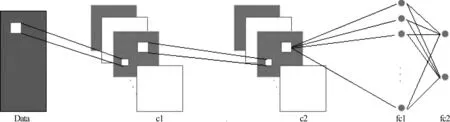
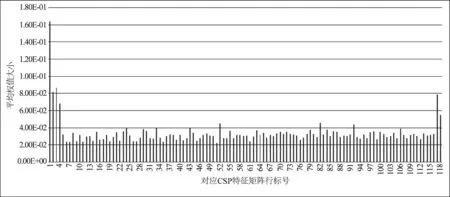
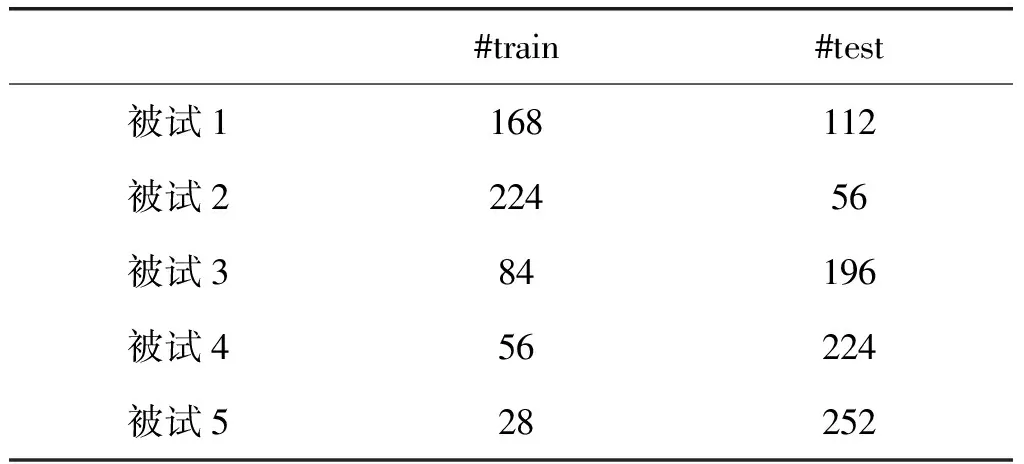
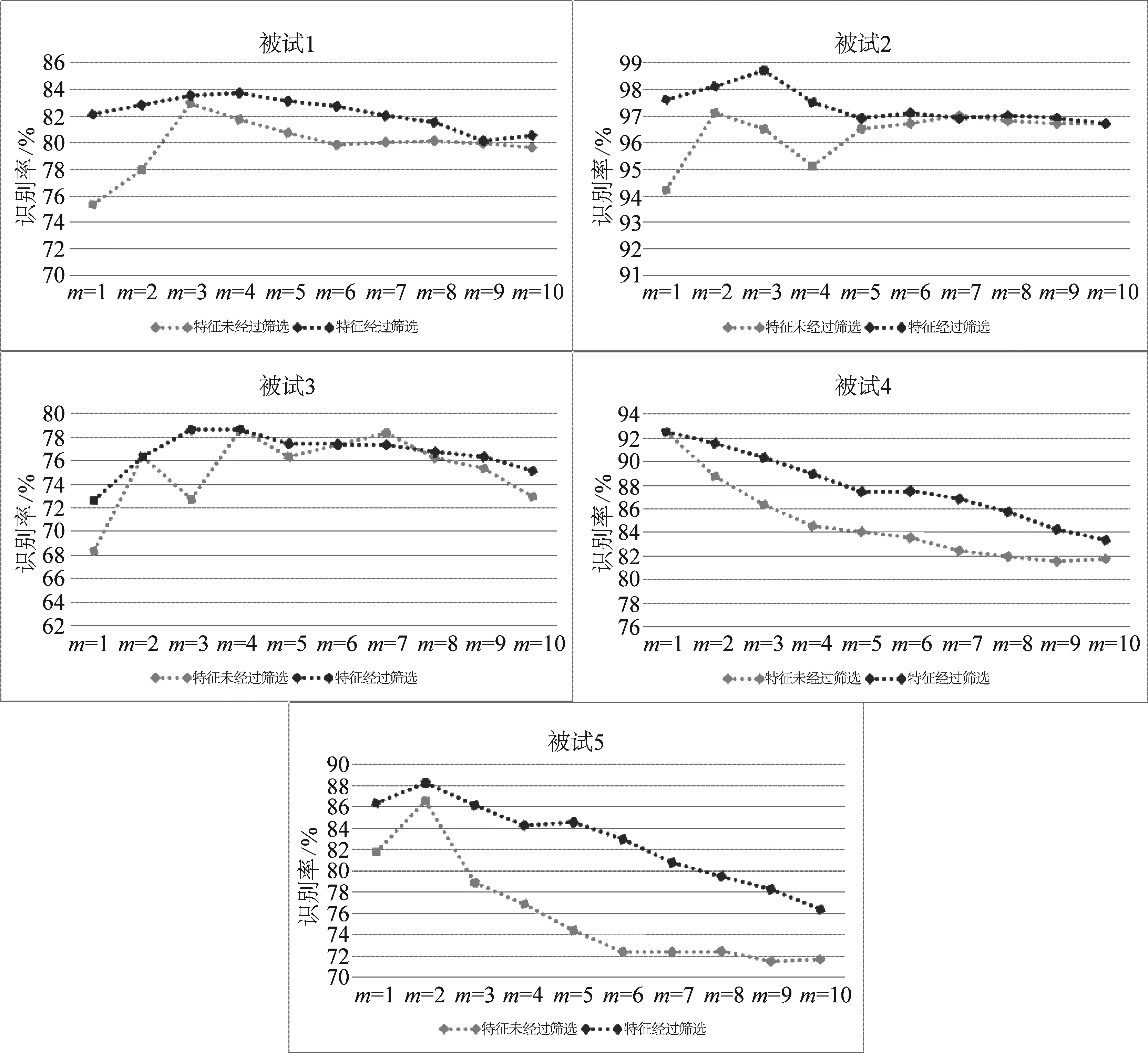
可选择ZM×N的前m行和后m行(2m 由CSP算法的原理可知,对于算法生成的CSP特征矩阵,其信息是不等效的。特征信息主要集中在特征矩阵的头部和尾部,而中间的特征信息不明显。但是,在传统的CSP算法中,并没有给出如何选取头尾特征行数,即选取m值的方法。因此如何选择m,是一个关键性的问题。选择的m值过小,特征信息并不足够,导致识别率不够高;选择的m值过大,会有冗余的信息,导致训练难度增大,训练的速度减慢,进而导致识别率不够理想。 卷积神经网络(Convolution Neural Network,CNN)是一种高效的识别方法,它可以直接输入原始特征空间,并在网络内部对特征的进行提取和进一步优化,因此再解决高维度特征的分类问题具有很好的效果。相比于全连接网络,卷积神经网络具有两个特性,分别是权值共享和局部感知。权值共享指的是同层某些神经元之间的连接权值是共享的,局部感知指的是神经元之间的连接并非是全连接,是局部的。这两个特点能够极大减少连接权值的数量,从而减少了模型的复杂度。卷积神经网络的基本结构如图2所示。 图2 CNN网络结构图 卷积操作是CNN中最为重要的操作,是用来提取某种特征。在卷积层中,一般设置多个不同的卷积核来对输入进行操作从而获得不一样的特性,进而达到提取特征的效果。具体计算过程如下,首先将卷积核的权值与上层数据进行卷积运算,然后使用激活函数进行处理并加上偏置值,于是可以得到一种特征表达。进而通过不同的卷积核便可以得到不同的特征表达,在不断的迭代训练过程中有效的特征便会得到强化从而达到提取特征的目的。 具体来说,可用如下公式表示卷积层的卷积运算的过程: (11) 在网络的训练过程中,为了能够使网络有效收敛,需要设置一个loss函数,也就是需要优化的目标函数。因此可以设置目标函数为数据集所有数据的loss平均值。进而可以得到如下loss函数: (12) fW(x)计算的是数据X上的loss,D为整个数据集。方法是,求出所有样本X(i)的loss值并且求和,最后再求均值。均方根误差作为一种常用的loss函数,求得是所有样本估计值和预测值的欧氏距离的平方的均值。另外,r(W)是为了减弱过拟合现象而设置的正则项。 (13) Wt+1=Wt+Vt+1 (14) 学习率为α,μ为上一次梯度的权重值,表示之前梯度下降的方向对现在梯度方向影响。 本文提出的CNN与CSP相结合的脑电特征提取与识别方法,工作流程如图3所示。 在将原始脑电信号经过预处理后,通过CSP空间变换得到相应的特征矩阵。构建CNN网络进行特征矩阵学习,获得CNN网络全连接层的权值矩阵,并对其进行分析,定义了CSP矩阵特征筛选准则,得到降维高效的EEG特征集F;计算特征集F规模并构建一个新网络CNN分类器。 本文的分析方法中,通过CSP空间变换得到相应的特征矩阵。将得到的特征矩阵用CNN进行学习,进一步分析其全连接层的权值情况从而对特征矩阵进行二次特征提取。 图3 基于CNN的自适应CSP特征提取方法脑电分析框架图 在对特征矩阵的学习过程中,本文所使用的卷积神经网络结构如图3所示。整个CNN网络结构由5层组成,第1层为输入层,第2、3层为卷积层,第4、5层为全连接层。 CNN网络的具体参数如下: (1)第一层(Data):输入层。输入为经CSP变换后的特征矩阵,维度为M×N,M为电极数目,N为每一个电极上的特征点数。 (2)第二层(C1):该层为卷积层,该层设置32个卷积核,卷积核的大小为1×50,卷积步长为1×2,使用ReLU激活函数。为了在特征筛选阶段对CSP特征矩阵的特征进行进一步筛选,在这里不在电极的维度上进行卷积,仅在特征点的维度上进行卷积。 (3)第三层(C2):该层为卷积层,主要是对第二层的特征图进行进一步的卷积,提取相应的特征。 该层也设置为32个卷积核,卷积核的大小为1×20,步长为1×2,使用ReLU激活函数。 (4)第四层(FC1):该层为全连接层,神经元的个数为1000个,作用是配合卷积层形成对脑电信号的分类。 (5)第五层(FC2):该层也为全连接层,共有2个神经元,代表了二分类问题。 网络中各层的具体参数是由实验择优确定。 在使用CNN对特征矩阵进行学习之后,为了对筛选特征的有效性进行验证,对CNN中全连接层的权值进行分析。我们展示第4节运动想象实验中的2号被试一个实验结果,对CNN全连接层的权值进行可视化,可得到如4所示。2号被试的原始脑电数据大小为118*200,其中118代表118个电极,200代表每个电极上的采样点数是200。经过CSP变换后得到特征矩阵大小为118*200,再经过CNN学习,图4为全连接层对应第二层卷积层输出的权值连接图像(所有卷积核求平均,具体算法在3.2节),维度为118*29(为了显示效果,对图片进行了横向放置)。 从图4中可以观察到大的权值(亮的部分)主要集中在前4列和后2列,分别对应CSP矩阵前4行和后2行特征。表明CSP矩阵的有效特征信息主要集中在这几行。为了对比图4中每一列的权值大小差异,分别对每一行的权值进行叠加平均,并绘制柱状图,如图5所示。 由图5观察可得,亮度大的权值主要集中前面4列和后面2列,这说明有效的特征主要集中在CSP特征矩阵的头部和尾部。可见,对CSP处理后的特征矩阵进行有效选择可以得到更加有效的特征。 图4 CNN全连接层可视化图像 图5 CNN全连接层对应CSP矩阵各行特征的平均权值大小 我们知道对于CSP的特征矩阵ZM×N,有效的信息集中在矩阵的前m行和后m行,一般选择2行或者3行特征,但是对于具体问题,m值的确定是个难点问题,定义准确求取m值方法是CSP技术发挥最佳性能的关键。因此,本文提出基于CNN的CSP特征筛选算法,主要思路为,将特征矩阵输送到CNN中进行学习,进而提取其全连接层的权值,通过其权值大小的分布来判断特征矩阵中哪些部分对分类更加有效果,从而对部分特征进行筛选。 具体步骤如下: 首先求得有益加权权值矩阵。设CNN中全连接层接受的输入特征图数量为s,特征图的维度为n×l,且有t层全连接层,每一层全连接层分别用W1,W2,…,Wt表示,且节点数目为k1,k2,…,kt。第t层全连接层,有kt个节点,在二分类问题中,kt为2。 当t=1时,即只有1个全连接层,即W1(维度为[s×n×l,kt])可作为有益加权权值矩阵。 当t>1时,为求得最有效的权值矩阵,对每一层,我们以下一层权值为权重对该层权值进行加权,即有如下公式: W=W1×W2×…×Wt (15) 则W的维度为[s×n×l,kt],其中s为最后一层卷积层的卷积核数量,且卷积出来的特征图大小为n×l,kt为第t层的节点数目,因为二分类问题,kt为2,且[s×n×l,1]与[s×n×l,2]权值的趋势变化是相反的。然后将得到的W矩阵的第2个维度的第1行进行重排列得到[s,n,l]大小的矩阵W′。 矩阵W′可以看成是s幅n×l权值图像。我们对每一幅图像都进行取绝对值操作,即求得一幅图中所有值对平均值的偏差程度,这样会使有效的权值包括正相关权值和负相关权值变为大值,而无效的权值会趋近于0。进而对矩阵W′的s幅图像求平均得: (16) 对矩阵T,便可以求得每一行的标准差,i的取值范围是(1≤i≤n): (17) (18) P为一个列向量,表示CSP特征矩阵中每一行的偏差程度,偏差程度越大说明这一行的特征越明显。可以观察到CSP特征矩阵中的列向量P有如下特征,中间的值趋近于0,而两边值较大。 可以对P的大小进行排序并选取前m′行,使得P(i)≥φ(φ为阈值,我们认为偏差标准值的0.5为有效特征,因此取φ=0.5)。 对应选择CSP矩阵中m′行做为特征集F。 具体如算法1所示。 算法1 基于CNN的CSP特征筛选算法 对于CSP特征筛选的过程,首先将全部的CSP特征矩阵输送到一个CNN中进行识别,得到收敛后的CNN网络权值,运用CSP特征筛选算法,即可从CNN网络权值的分布计算得到最优的特征集。 我们在公开数据集(BCI Competition Ⅲ的Data set IVa数据集)[25]的运动想象数据集上进行了方法测试,并与传统CSP方法、sCSP方法和KLCSP方法进行比较。 BCI Competition Ⅲ的Data set IVa数据集是由Fraunhofer FIRST、Intelligent Data Analysis Group (Klaus-Robert Müller, Benjamin Blankertz)和Campus Benjamin Franklin of the Charité-University Medicine Berlin, Department of Neurology, Neurophysics Group (Gabriel Curio)提供的一个公共数据集。 此数据集是从五个健康被试身上采集下来的。被试坐在舒适的椅子上,双臂放在扶手上。被试需要观察3.5 s的视觉提示,然后被试进行运动想象,想象的内容为两个类型中的一个:(R)右手运动,(F)右脚运动,然后被试进行1.75~2.25的休息。每名被试需要做280次重复实验。 本数据集为含有118个电极的连续脑电,每名被试的训练集与测试集数量分布如表1所示。 表1 训练集与测试集数量分布表 为了与相应研究中的数据处理方法保持一致,本实验使用每次试验开始后0.5到2.5 s的脑电信号数据作为一个样本数据[26],然后使用8至30 Hz的单带通滤波器对脑电数据进行滤波。最后,选取于运动想象任务相关的两个频带mu(8~12 Hz)和beta(18~25 Hz)节律[27]。 对经过预处理后的脑电数据通过CSP算法提取相应的特征。具体操作如下。 首先将原始EEG数据按照类别进行分段。一次脑电实验中的任务数据表示为一个矩阵D,D的维度为M×N,M为电极数目,N为电极上的采样点数。可将D根据类别分段为D1和D2,D1表示第一类样本数据,D2表示第二类样本数据。 根据CSP算法的步骤,然后对D1和D2分别求得协方差矩阵的期望并进行加和,然后再进行正交白化变换并且同时对角化,计算投影矩阵并进行投影得到相关的特征矩阵ZM×N。 为了验证由基于CNN的CSP特征筛选算法提取出来的最优特征集的识别效果,进行如下对比实验。 首先测试全部被试分别在不同m值(即对称选取CSP特征矩阵的头部和尾部各m行,由CSP矩阵的性质,取1≤m≤10)的情况下的识别率,为了防止网络的随机初始化给网络的识别率带来影响,因此,对于每一个被试的每一个m值,训练并测试5次,算出识别率的平均值作为真正的识别率。 然后运用基于CNN的CSP特征筛选算法计算出每一个被试的最优特征集。 得到特征集后,为了验证本文方法筛选的特征的有效性,分别对应于不同m值,选取相同数量的最优特征作为特征集,并再次构建CNN分类器对特征集进行分类识别。为了提高训练的效率,加快收敛速度,使用的CNN分类器与CNN学习过程的网络参数大致相同,并且复用卷积核权值和全连接层对应特征的权值作为初始值进行训练。 具体的识别率对比如图6所示,下图的内容为不同被试在不同m值下的识别率。 由图6可以观察到,本文方法选择出来的特征集,相比于原CSP算法直接提取特征矩阵前m行和后m行的方法,具有很好的分类识别性能,能够达到更高的识别率。说明本文方法能够有效优选出最佳特征。由图中还可以观察到,本文方法选取的特征集得到识别率随着特征数量的增多呈现先增加后减小的趋势,这说明随着有效特征数量的增多,识别性能不断增加,但增加到一个程度,即较有效的特征已经被筛选完毕,再增加特征只会增大系统的负担,导致识别率的降低。 对五名被试的观察可以发现,前三名被试的识别率比较稳定,而后两名被试随着特征数量的增多识别率降低较为明显。我们推测是因为训练样本数较少的缘故,第4名被试的训练集只有56个样本,而第5名只有28个样本,在这种情况,很容易出现训练集过拟合,而同时测试集识别率并不高的情况。由于每次训练设置的网络初始值是随机的,在网络收敛后测试集的识别率会有较大波动。我们在实验过程中观察到被试4和5在特征较多的情况下出现训练集识别率达到100%而测试集识别率相差较大的情况。而低的识别率会拉低平均识别率,这就是被试4、5随着特征数量的增多平均识别率出现较大下滑的原因。 图6 五名被试在不同m值下特征经过筛选和未经过筛选情况下的识别率 对同一被试由基于CNN的CSP特征筛选算法选择出来的最优特征集所对应的识别率基本上为最优识别率,因此基于CNN的CSP特征筛选算法能够有效优选出最佳特征。 为了验证本方法的有效性,在BCI Competition Ⅲ 的 Data set IVa数据集上与一些其他方法进行对比实验。本文方法与传统CSP方法、sCSP方法[22]和KLCSP方法[23]进行比较,这些方法的识别结果均是根据文献中的记录而来。在数据训练的过程中,需要为每一名被试单独训练一个模型,并通过此模型来统计对应被试的识别率。 现将各方法的结果总结如表2所示。 可以看到,CNN与CSP相结合的脑电特征提取与识别方法相比经典CSP以及其一些改进方法在识别率上有一定程度的提高。与sCSP方法和KLCSP方法相比,本文方法的平均识别准确率分别提升了3.2%和2.4%,且本方法使用了全部的原始数据,未剔除任何不佳的样本数据。可以说明本文方法在对运动想象数据进行识别方面是有很好的效果。 表2 不同实验方法识别率对比表 表3 BCI Competition III的竞赛数据集IVa上的最好分类结果 此外,在BCI Competition III的竞赛数据集IVa上的最好分类结果如表3所示。本文的特征提取和分类算的最优结果为88.3%。与竞赛的第二优胜者识别率有5%的提高。虽不及排名第一的清华大学识别结果,但系统在采用的特征数量和系统复杂性方面具有很好的优势。 本文提出了一种CNN与CSP相结合的脑电特征提取与识别方法。首先在经过预处理的原始脑电信号上进行CSP空间变换得到相应的特征矩阵;其次,构建CNN网络进行特征矩阵学习,获得 CNN网络全连接层的权值矩阵,并对其进行分析,定义了CSP矩阵特征筛选准则,得到了低维高效的EEG特征集F;最后,根据特征集F构建一个CNN网络分类器进行分类。本文方法在BCI2005Ⅳa竞赛数据集上进行实验,首先通过CSP特征筛选算法的验证实验观察到得到的特征集F都是最优的,从而验证了算法选取的特征集的有效性。然后通过与其他方法的对比实验发现,相比于sCSP和KLCSP方法,本文所提出的方法平均识别准确率分别提升了3.2%和2.4%。而且,本方法使用了全部的原始数据,未剔除任何不佳的样本数据,更加适用于脑机接口系统。本文方法结合了时间、空间的特征信息,而且引入了根据结果对特征进行二次选择的新观点,为脑电的特征提取问题提供了一个新的思路。 [1] Guger C, Allison B, Ushiba J. Recent Advances in Brain-Computer Interface Research—A Summary of the BCI Award 2015 and BCI Research Trends[M]∥Brain-Computer Interface Research. Springer International Publishing, 2017: 131-136. [2] Holz E M, Botrel L, Kaufmann T, et al. Long-term independent brain-computer interface home use improves quality of life of a patient in the locked-in state: a case study[J]. Archives of physical medicine and rehabilitation, 2015, 96(3): S16-S26. [3] Hsu W Y. Brain-computer interface: The next frontier of telemedicine in human-computer interaction[J]. Telematics and Informatics, 2015, 32(1): 180-192. [4] Doud A J, Lucas J P, Pisansky M T, et al. Continuous three-dimensional control of a virtual helicopter using a motor imagery based brain-computer interface[J]. PloS one, 2011, 6(10): 263-296. [5] Gao X, Xu D, Cheng M, et al. A BCI-based environmental controller for the motion-disabled[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2003, 11(2): 137-140. [6] Xu N, Gao X, Hong B, et al. BCI competition 2003-data set IIb: enhancing P300 wave detection using ICA-based subspace projections for BCI applications[J]. IEEE Transactions on Biomedical Engineering, 2004, 51(6): 1067-1072. [7] Bashar S K, Hassan A R, Bhuiyan M I H. Identification of motor imagery movements from eeg signals using dual tree complex wavelet transform[C]∥Advances in Computing, Communications and Informatics (ICACCI), 2015 International Conference on. IEEE, 2015: 290-296. [8] Hassan A R, Bhuiyan M I H. A decision support system for automatic sleep staging from EEG signals using tunable q-factor wavelet transform and spectral features[J]. Journal of Neuroscience Methods, 2016, 271: 107-118. [9] Boonnak N, Kamonsantiroj S, Pipanmaekaporn L. Wavelet transform enhancement for drowsiness classification in EEG records using energy coefficient distribution and neural network[J]. International Journal of Machine Learning and Computing, 2015, 5(4): 288. [10]Li P, Wang X, Li F, et al. Autoregressive model in the Lp norm space for EEG analysis[J]. Journal of Neuroscience Methods, 2015, 240: 170-178. [11]Fang Y, Chen M, Zheng X. Extracting features from phase space of EEG signals in brain-computer interfaces[J]. Neurocomputing, 2015, 151: 1477-1485. [12]Hsu W Y. Assembling a multi-feature EEG classifier for left-right motor imagery data using wavelet-based fuzzy approximate entropy for improved accuracy[J]. International Journal of Neural Systems, 2015, 25(8): 1550037. [13]Meyer M C, Janssen R J, van Oort E S B, et al. The quest for EEG power band correlation with ICA derived fMRI resting state networks[J]. Frontiers in Human Neuroscience, 2013, 7: 315. [14]Dan'ko S G, Gracheva L V, Boǐtsova I A, et al. Induction of emotional states during oral reading of texts with different emotional valence and EEG power dynamics in frequency bands beta2 and gamma[J]. Fiziologiia Cheloveka, 2011, 37(5): 46. [15]Zheng W L, Lu B L. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks[J]. IEEE Transactions on Autonomous Mental Development, 2015, 7(3): 162-175. [16]Fitzgibbon S P, DeLosAngeles D, Lewis T W, et al. Automatic determination of EMG-contaminated components and validation of independent component analysis using EEG during pharmacologic paralysis[J]. Clinical Neurophysiology, 2016, 127(3): 1781-1793. [17]Burger C, van den Heever D J. Removal of EOG artefacts by combining wavelet neural network and independent component analysis[J]. Biomedical Signal Processing and Control, 2015, 15: 67-79. [18]Koles Z J. The quantitative extraction and topographic mapping of the abnormal components in the clinical EEG[J]. Electroencephalography and Clinical Neurophysiology, 1991, 79(6): 440- 447. [19]Ramoser H, Muller-Gerking J, Pfurtscheller G. Optimal spatial filtering of single trial EEG during imagined hand movement[J]. Rehabilitation Engineering, IEEE Transactions on, 2000, 8(4): 441- 446. [20]Koles Z J. The quantitative extraction and topographic mapping of the abnormal components in the clinical EEG[J]. Electroencephalography and Clinical Neurophysiology, 1991, 79(6): 440- 447. [21]Ramoser H, Muller-Gerking J, Pfurtscheller G. Optimal spatial filtering of single trial EEG during imagined hand movement[J]. Rehabilitation Engineering, IEEE Transactions on, 2000, 8(4): 441- 446. [22]Samek W, Vidaurre C, Müller K R, et al. Stationary common spatial patterns for brain-computer interfacing[J]. Journal of Neural Engineering, 2012, 9(2): 026013. [23]Arvaneh M, Guan C, Ang K K, et al. Optimizing spatial filters by minimizing within-class dissimilarities in electroencephalogram-based brain-computer interface[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(4): 610- 619. [24]Lawrence S, Giles C L, Tsoi A C, et al. Face recognition: A convolutional neural-network approach[J]. Neural Networks, IEEE Transactions on, 1997, 8(1): 98-113. [25]Dornhege G, Blankertz B, Curio G, et al. Boosting bit rates in noninvasive EEG single-trial classifications by feature combination and multiclass paradigms[J]. IEEE Transactions on Biomedical Engineering, 2004, 51(6): 993-1002. [26]Ang K K, Chin Z Y, Wang C, et al. Filter bank common spatial pattern algorithm on BCI competition IV datasets 2a and 2b[J]. Frontiers in Neuroscience, 2012, 6(2): 268-275. [27]McFarland D J, Miner L A, Vaughan T M, et al. Mu and beta rhythm topographies during motor imagery and actual movements[J]. Brain Topography, 2000, 12(3): 177-186.2.2 卷积神经网络原理
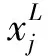
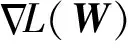
3 CNN与CSP相结合的脑电特征提取方法
3.1 CNN与CSP相结合的脑电特征提取方法工作流程
3.2 CNN学习与权值矩阵分析


3.3 基于CNN权值矩阵特性的CSP特征筛选准则
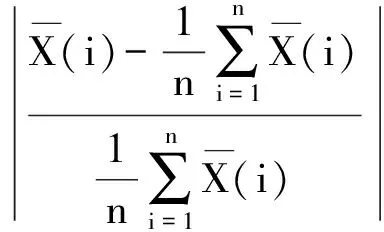

4 实验及结果分析
4.1 实验数据集
4.2 数据预处理
4.3 CSP算法处理
4.4 最优特征集的验证实验及识别结果
4.5 CNN与CSP相结合的脑电特征提取与识别方法的对比实验及结果


5 结论

