Alpha稳定分布噪声下的舰船识别分析

姚 祺 王 彬 张俊林

(解放军信息工程大学，河南郑州 450001)

1 引言

舰船在航行或作业时,推进器和各种机械都在工作,它们产生的振动能量通过船体向水中辐射形成舰船辐射噪声,它本身是舰船上众多声源的综合响应,主要特征信息一般由辐射噪声在单位频率范围内平均能量的连续谱信息和机械震动源、水下螺旋桨产生的具有固定周期的线谱信息构成。连续谱强度会随水文环境和传播距离而变化,一般低频段上升而在高频段下降,该临界频率又称连续谱谱峰频率。舰船吨位越大,航速越快,临界频率越高。线谱信息幅度高,在低频段稳定存在,螺旋桨线谱是以叶频为基频的倍频谐波族。连续谱的波动起伏和线谱的倍频特性都可以作为特征提取的差异量用于舰船识别,但都易被环境噪声掩盖,无法有效获取。

为了有效地提取舰船辐射特征,以往方法多是基于不同舰船连续谱的波动起伏和线谱的倍频特性等特征差异作为识别依据。近些年来,基于舰船辐射噪声的目标识别得到了新的发展,Pan Y从完备总体经验模态分解(Complementary ensemble empirical mode decomposition)入手,配合小波阈值抑噪,相比传统的经验模态分解,分解出的固有模态函数线谱特征更加清晰[1]。Li Y X同样从经验模态分解的角度,求每阶固有模态函数的排列熵,组成新的特征向量成功区分了三类实测舰船噪声[2]。Mu L从生理感知的角度入手,使用耳蜗模型滤波器处理舰船辐射噪声,发现滤波器输出的信号线谱特征比传统调制谱法更加明显[3]。Wang Y针对舰船辐射噪声螺旋桨线谱基频峰值常比其谐频峰值小的特点,使用基于Duffing震荡方程的非线性混沌系统处理信号,成功提取了螺旋桨基频特征,即螺旋桨转速[4]。这些方法虽然有效,但都是在高斯型背景噪声条件下进行的。Chitre M在浅海声场分析时论证了海浪噪声等具有明显脉冲特性[5],这些短时的大幅度脉冲更符合Alpha稳定分布,由于Alpha稳定分布噪声二阶以上统计量趋近于无穷大,高斯背景下的常规阶次特征处理方法已然失效。为了解决这一问题,张安清利用正弦波模型简化的舰船辐射噪声模型,研究了在Alpha稳定分布噪声背景下使用分数阶统计量会有较好效果[6]。但是该方法存在分数阶次p的估计问题,即很难确定p的最佳值使得对背景噪声的抑制效果最好,同样对某类背景噪声下的舰船信号,其估出的最佳p值不一定适用于其他类别舰船辐射噪声。为了避免分数阶次的估计问题,本文在研究Alpha稳定分布相关特征的基础上,利用反正切非线性变换抑制背景噪声,再对抑噪信号提取1.5维谱特征,输入基于粒子群优化算法的支持向量机识别器,实验结果证明该方法可以有效地抑制背景噪声的干扰对舰船进行分类。

2 信号模型

由于舰船辐射噪声带宽范围较宽,主要集中在0～10 kHz范围内,以20 kHz为采样率fs,对接收信号进行采样,得到Alpha稳定分布噪声环境下被动声呐接收信号模型如下

y(k)=x(k)+n(k)

(1)

声呐接收信号为y(k),实际舰船辐射噪声信号为x(k),背景Alpha稳定分布噪声是n(k),k=1,2,…,N,N为采样点数。其中x(k)主要包括连续谱分量xc(k)和线谱分量xl(k),其时域波形的数学描述为[7]

x(k)=[1+a(k)]xc(k)+xl(k)

(2)

式中a(k)为周期调制波形,典型的舰船辐射噪声连续谱主要来自于螺旋桨空化噪声,其时域函数xc(k)近似于一系列随机幅度、周期性的高斯型脉冲,单个脉冲如下：

(3)

式中fs是采样率,σ是高斯方差,ξ是相互独立的幅度变量,则xc(k)数学模型可简化为

(4)

其中,dξ是脉冲间隔。在高频段,连续谱以6 dB的倍频程斜率下降,而在低频段与高频段之间存在谱峰频率f0,频率f0的值与舰船吨位、航速等特征有关。线谱主要来自于螺旋桨叶片的周期旋转和其周围的不规则流动,它是一种叶片速率谱,其频谱与螺旋桨叶片数和轴频转速直接相关,满足如下关系：

fm=m·n·s

(5)

其中n是螺旋桨叶片数,s是螺旋桨转速,m是谐波次数。于是舰船辐射噪声的线谱时域数学模型可以表示为

(6)

其中Am为幅度变量,M是谐波阶次。

背景噪声用n(k)表示,在实际中所遇到的海洋环境噪声(海浪噪声、风成噪声、生物群活动等)以及多种人为噪声均不是高斯分布的。这类噪声在实际采集中无法避免,它们的共同特点是噪声的某些瞬间幅度远远地高出其均值,具有非常显著的脉冲特性,且其统计密度函数具有较厚的拖尾,正符合分数低阶Alpha稳定分布过程的显著特征,其分布特征函数为[8]

φ(θ)=exp{jμθ-γ|θ|α[1+jζsgn(θ)ω(θ,α)]}

(7)

其中sgn(·)是符号函数

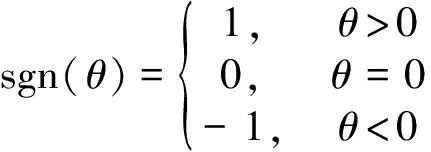
(8)

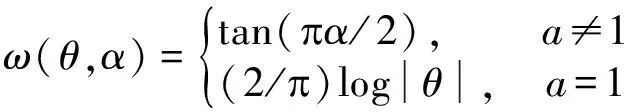
(9)

其中参数α(0<α≤2)称为特征指数,γ≥0为分散系数,ζ(-1≤ζ≤1)是对称参数,μ为位置参数,sgn(·)是符号函数。定义舰船辐射噪声和背景噪声混合信噪比MSNR。

(10)

3 Alpha稳定分布噪声下舰船辐射噪声特征提取

本文采用反正切变换的方法抑制Alpha稳定分布噪声对舰船辐射噪声的干扰,在抑噪信号的基础上提取1.5维谱特征,进行舰船识别,过程流程图如图1所示。

图1 舰船识别流程图

3.1 反正切非线性变换

低阶统计量虽然可以抑制噪声干扰,但其中分数阶阶次p对于某类未知特征的舰船辐射噪声,很难估计到最佳值。除此之外,由于舰船种类繁多,对某种环境下某类舰船辐射噪声估计出的最佳阶次p,常常并不同样最佳适用于其他舰船。所以本文选用反正切非线性变换的方法,避免阶次估计问题,抑制噪声干扰。

利用反正切函数可以将无穷区间映射到(-π/ 2,π/ 2)内,该特性可以很好抑制Alpha稳定分布噪声对舰船辐射噪声的影响。该非线性变换定义为[9]

(11)

对于信号f(y),将式(1)代入得

(12)

当信号模型混合信噪比较高时,式(12)可化为:

(13)

3.2 1.5维谱

反正切非线性变换可以抑制Alpha稳定分布噪声对舰船辐射噪声的影响,常规阶次的方法此时可以使用。由于舰船结构复杂,工作时声源繁多,选取稳定且突出的特征是选择的重要依据。连续谱特征是船上各辐射声源在单位频率范围内的平均能量综合体现,由于来源复杂,且易受环境噪声和传播损失的影响,很难有效恢复。船舶的叶频以及它们的谐频,通常通过调制线谱的形式存在于舰船辐射噪声中。这类线谱具有强度高、稳定性好、远程传输损失少的特点,是舰船识别的主要依据。功率谱特征计算量小,但是存在对噪声敏感,特征易被掩盖的问题。使用高阶统计量的方法可以有效地抑制接收信号中高斯成分的影响,但往往计算量大,且显示不够直观。1.5维谱作为高阶谱的一种特殊情况,它既可以突出螺旋桨线谱谐波族特征,又大大的简化了计算量。

对于信号模型的采集序列y(k),其三阶累计量c(d1,d2)的对角切片的Fourier变换为离散序列y(k)的1.5维谱C(w)。具体定义式如下[10]：

x(i)(k+d)e-jwd

(14)

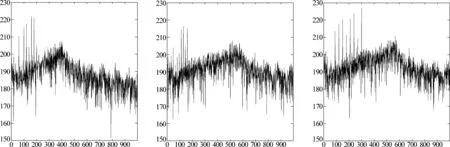
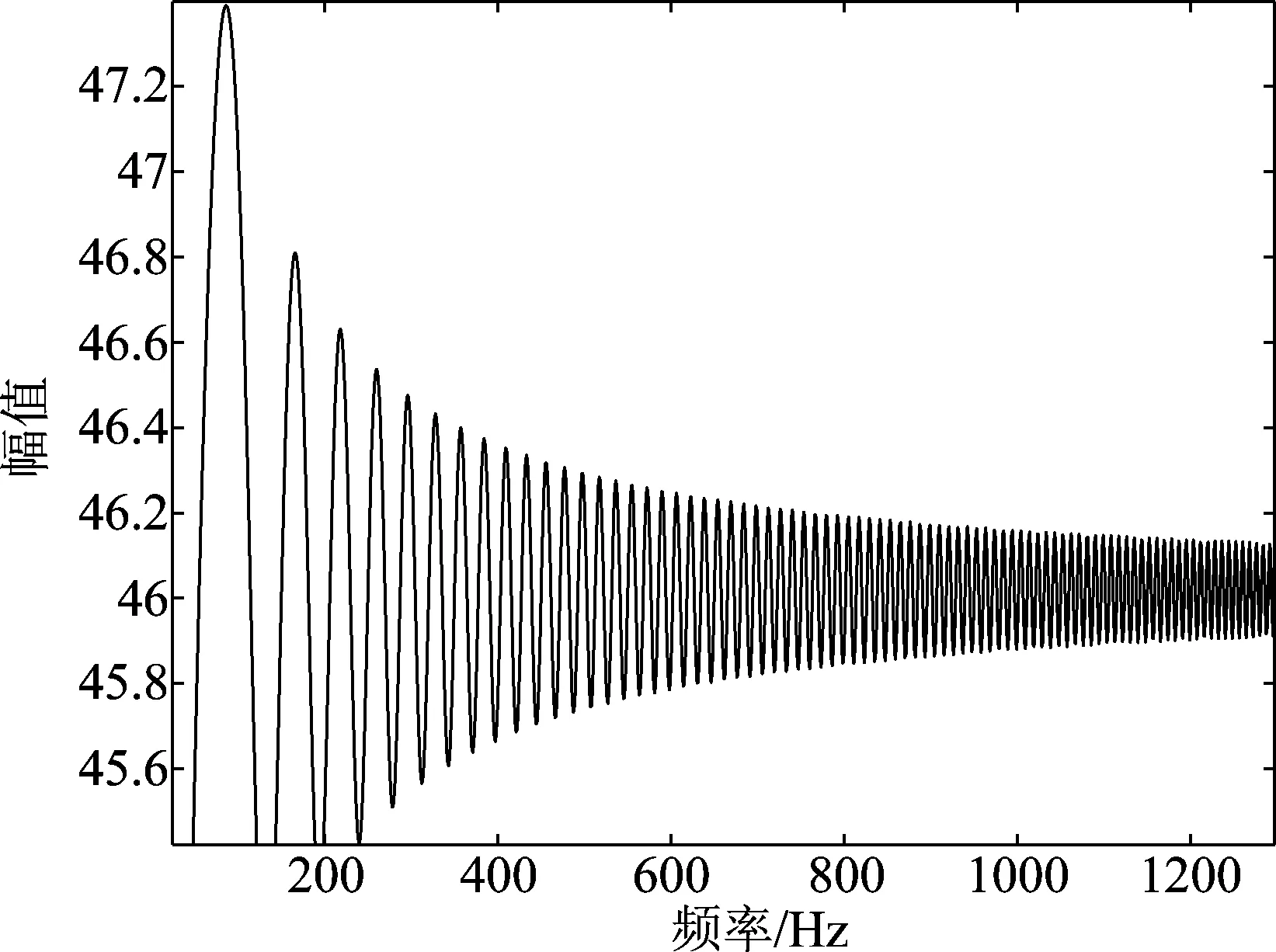
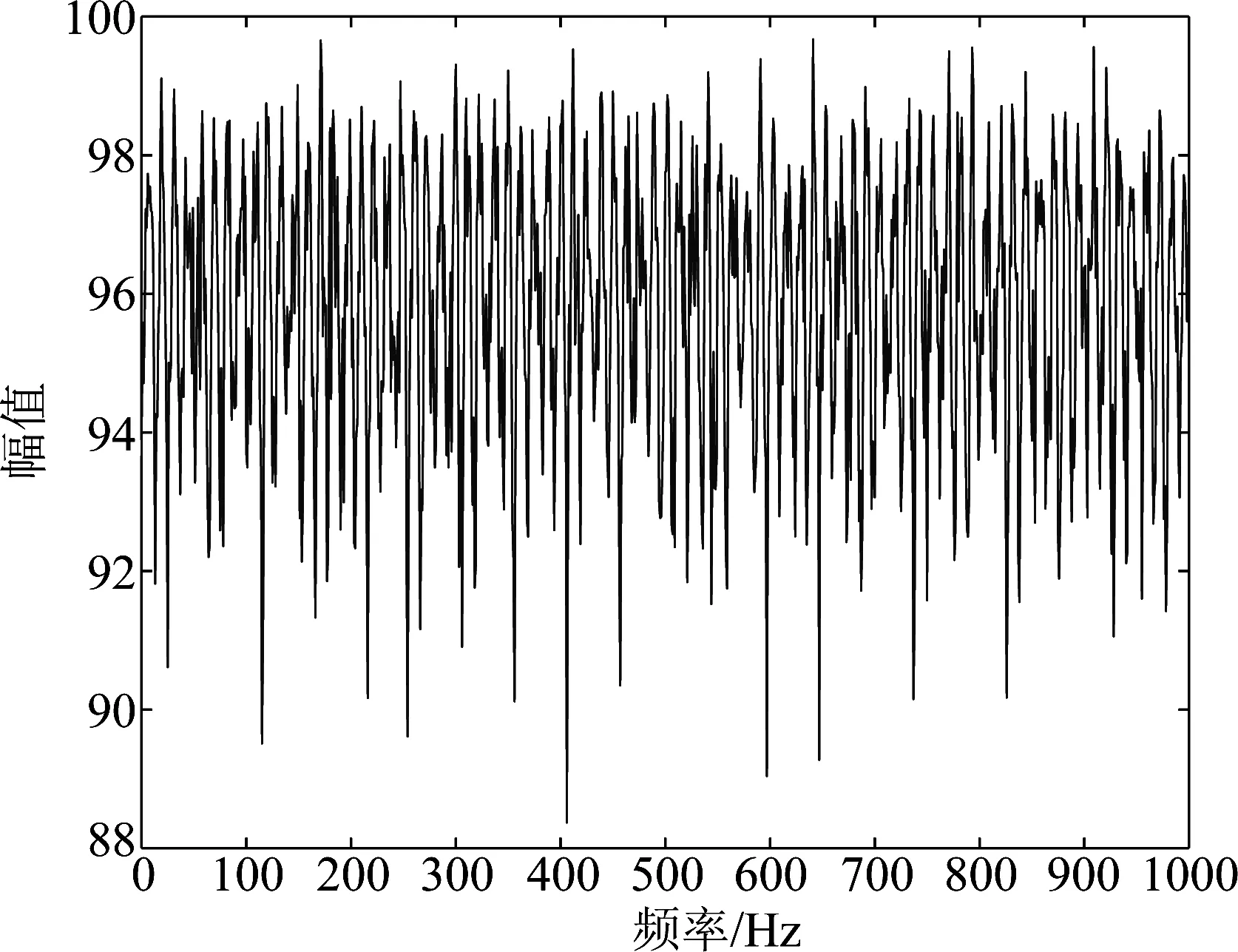
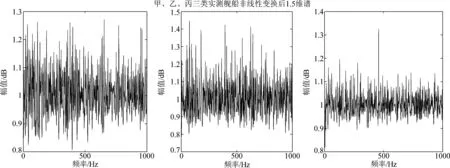
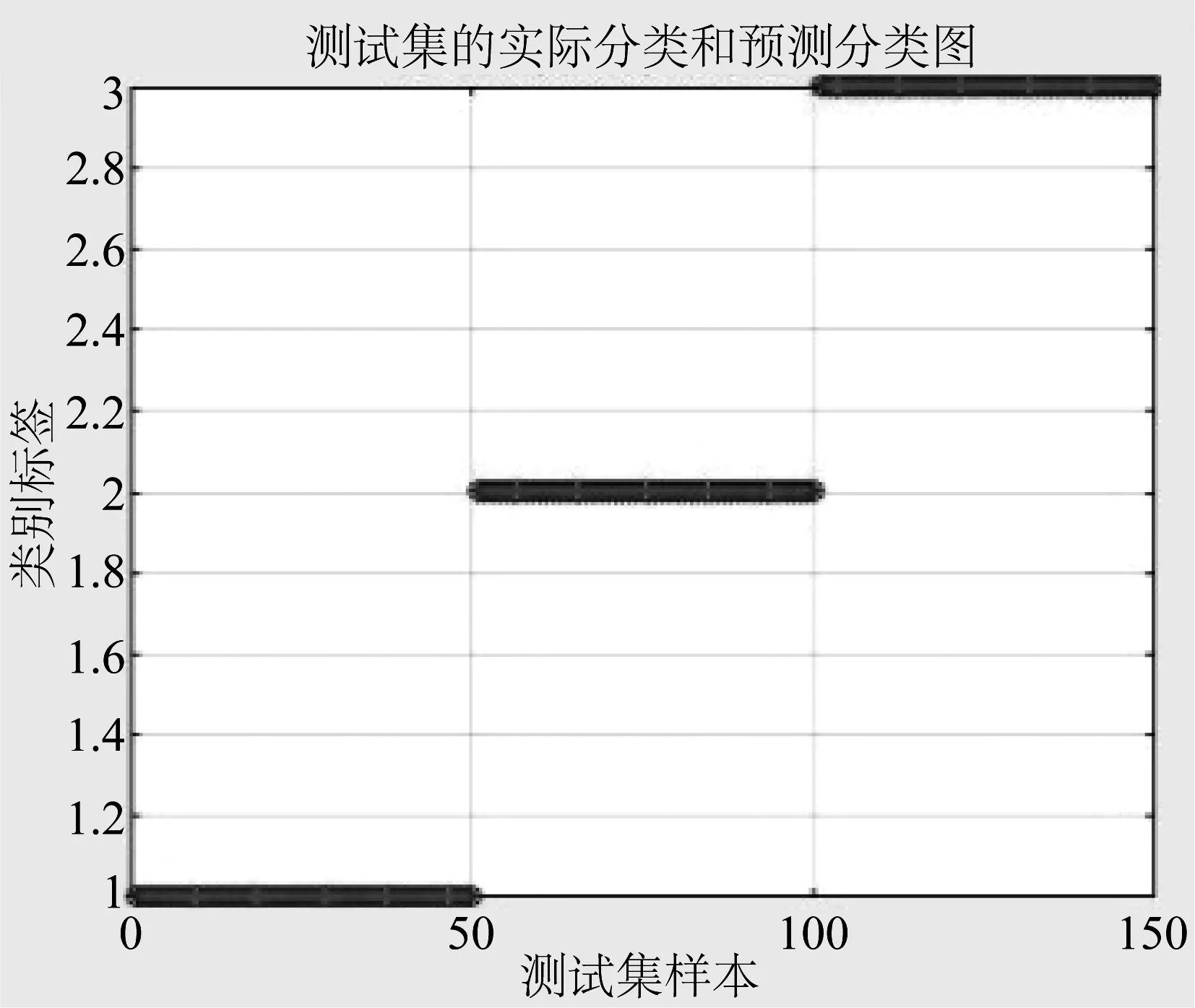
式中K,M将采集的N点数据分成K段,每段样本数为M,M1,M2是每段数据内序列标号k的阈值范围,M1=max(0,d),M2=min(M-1,M-1-d),i是各段标号,L是每段数据时延d可取的最大值,L

3.3 SVM识别

对于本文识别样本集A、B、C三类舰船辐射噪声仿真信号和线性调频信号D,在混合信噪比-10 dB～10 dB下构造不同背景噪声强度的含噪信号。使用反正切非线性变换抑制Alpha稳定分布噪声幅值,再使用1.5维谱提取特征,将信号1.5维谱在0至1000 Hz内的强度构成特征向量库。从库中每一混合信噪比下四类信号各随机抽取10组特征向量,在-10 dB～10 dB范围内,共有40×21=840组特征向量,构成训练样本集矩阵。训练样本标签A类舰船标签为“1”,B类舰船标签为“2”,C类舰船标签为“3”,D信号标签为“4”。从库中同一混合信噪比下四类信号各随机抽取25组特征向量,共有4×25=100组特征向量,构成测试样本集矩阵。标签设置方法同训练样本集。

支持向量机通过非线性变换将输入的特征向量映射到高维空间,在高维空间寻找最优分类面,对于高维度、小样本的信号识别问题具有良好的性能,结合粒子群算法搜索策略,核函数参数可以快速收敛到最优值。目前该方法在信号识别领域已有较成熟的应用,同样适用于本文舰船辐射噪声信号的识别。对于输入的特征向量组X1,X2,…,Xkν,kν是特征向量组数,其中每组特征向量Xi={xi(1),xi(2),…,xi(Nν)},i∈[1,kν],Nν是特征维度,SVM输出分类决策函数为：

(15)

(16)

νi+1=wνi+c1r1(pBesti-xi)+c2r2(gBesti-xi)

(17)

xi+1=xi+νi

(18)

w是惯性权重系数,一般随着迭代次数如式(18)所示递减,起着平衡全局搜素与局部搜索的作用,一般在[0.9,0.4]范围内伴随着迭代线性递减,参数学习因子c1控制着参数局部搜索能力,学习因子c2则控制着参数全局搜索能力。C为标签类别个数,g为当前世代数,G为迭代总世代数。通过迭代搜索参数pBesti和gBesti满足分类适应度fitness最大,适应度公式为[12]：

(19)

式中Mpso是粒子个数,本文识别器初始化参数如表1。具体算法流程图如图2所示[13]。

表1 粒子群优化初始参数表

4 仿真结果分析

对于仿真信号的识别样本集,包含A、B、C、D四类仿真信号,其中信号A、B、C为设计的三类舰船辐射噪声仿真信号,其物理特征如表2。

表2 舰船辐射噪声仿真参数表

三类舰船频域图特征如图3所示。

仿真信号D为基带线性调频信号,它可看作水声信号中舰船等物体加速运动运动是辐射声波的模拟,作为识别集中的信号之一,其仿真图如图4所示。

图2 SVM识别算法流程图

在丰富的噪声背景下,常规阶矩的舰船特征识别系统鲁棒性减弱甚至不能工作,以MSNR=5 dB噪声环境下A类舰船频域特征为例如图5所示。

由图5明显看出此时A类舰船特征已不再明显,无法直接作为舰船识别的依据。针对这一情况本文采用非线性变换的方法降低Alpha稳定分布噪声的影响。同样以A类舰船MSNR=5 dB Alpha噪声背景为例,通过非线性变换后辐射噪声频域图如图6所示。

通过图6可以看出,非线性变换可以有效的抑制Alpha噪声的影响,大致恢复出原辐射噪声的连续谱与线谱特征,为我们Alpha稳定分布噪声环境下舰船识别的处理提供了思路。在非线性变换抑噪的基础上,针对仿真舰船A功率谱特征进行螺旋桨线谱提取分析,得到的结果如图7所示。

对比图5,由图7仿真结果可以明显看出,非线性变换的方法有效地恢复了舰船辐射噪声的频域特征,但是由于舰船辐射噪声中部分连续谱峰值较高以及噪声的影响,通过功率谱提取螺旋桨线谱特征,会在倍频线谱之外出现峰值,而且部分线谱峰值,如20 Hz、40 Hz、80 Hz等处幅值不太明显,因此需要引入高阶累积量来突出螺旋桨线谱成分。相对于功率谱,1.5维谱由于可以突出螺旋桨倍频线谱特征,相对于其他阶次高阶谱简化了计算,常用来满足实际线谱检测的应用要求。针对MSNR=5 dB Alpha稳定分布噪声环境下,A类舰船辐射噪声,使用反正切非线性变换抑制噪声后,1.5维谱特征如图8所示。

图3 三类舰船辐射噪声仿真信号功率谱图

图4 仿真信号D时、频域图

图5 MSNR=5 dB A类舰船辐射噪声仿真信号功率谱图

图6 MSNR=5 dB A类舰船辐射噪声仿真信号非线性变换后功率谱图

图7 A类舰船功率谱线谱

图8 MSNR=5 dB A类舰船辐射噪声仿真信号非线性变换后1.5维谱图

相对于图6、7功率谱,1.5谱有着更明显的线谱倍频谱峰,并抑制了“伪峰”的出现,此时,将0～1000 Hz频带内的1.5维谱频率响应作为样本特征,可以有效地区分不同种类舰船。

针对仿真信号A、B、C、D,在Alpha稳定分布背景噪声下,常规的基于二阶或者更高阶的特征提取方法,已不适用。如何在噪声环境下有效地恢复舰船辐射噪声特征,主要采用两种思路,一是使用分数阶统计量,选用分数阶谱；二是通过非线性变化的方式抑制噪声影响在适用常规阶次的谱分析方法。本文针对A、B、C、D四类仿真信号,分别使用功率非线性变换功率谱、非线性变换1.5维谱四种方法提取特征。选用4.3节的方法构造包含840组特征向量的训练矩阵,每组特征向量包含信号在各方法下0至1000 Hz的频率响应强度信息,输入SVM支持向量机通过粒子群优化的方法训练识别参数。然后选用4.3节的方法构造单一信噪比下包含100组特征向量的测试矩阵,通过识别率高低比较各特征提取方法的识别效果。

如图(a)是将信号不作抑噪处理,直接提取功率谱特征输入识别器的识别结果。图(b)是采用非线性变换抑制噪声影响,再提取功率谱特征输入识别器,得到的识别效果,图(c)是在图(b)的基础上,进一步提取1.5维谱特征输入识别器,得到的识别效果当样本MSNR取-10至10 dB时,各方法识别率曲线如图9所示。

由图(a)可知,囿于噪声影响,粒子群优化算法虽然可以将识别率不至于45%而是提高到50%以上,但是随着信噪比的提升,识别率的提高并不明显,这是因为常规的二阶矩无法正常还原舰船辐射噪声频域特征导致的。由图(b)可知非线性变换可以有效地抑制Alpha稳定分布噪声,使得基于功率谱等二阶统计量的方法恢复性能。由图(b)、(c)比较可知,通过反正切非线性变换抑制噪声影响,此时再使用功率谱或高阶谱的方法,可以得到较好的识别效果,由于1.5维谱可以有效的增强舰船辐射噪声螺旋桨线谱倍频关系,在-7 dB时便可以将识别率提升到90%以上。

最后，利用互联网网站“www.dosits.org oalib”舰船甲、乙、丙三种实测辐射噪声进行分析处理，下载信号为mp3文件，三艘舰船甲、乙、丙信号采样率为11 kHz，三组信号的采样点数在1100160—1169260之间，对接收的每类信号进行5倍的降采样，此时采样率降为2.2 kHz，从而将每类接收信号初步分成5组，三类舰船共得15组降采样信号，每组信号采样点数为220000个。针对每组长度220000的信号再平均分成20份，如此将三类信号分了100组，每组信号持续5 s，采样点数长度为11000，最终得到300组处理信号样本。最后针对分的每组实测信号，进行反正切变换后的1.5维谱特征提取，特征如图10所示。

图9 各方法不同信噪比下识别率

图10 三类实测舰船辐射噪声非线性变换后1.5维谱图

由图10可知甲、乙、丙三类舰船的1.5维谱有效的将某些频率上的分量突显了出来。这些分量主要代表着舰船辐射噪声线谱为主的信息,它主要来自于螺旋桨桨拍、机械轴承、齿轮旋转等周期性运动,三类舰船各有区别,因此可以作为特征依据输入识别器。

识别器训练过程中,粒子群优化参数初值仍选用表2内容。当迭代次数G=200时,20个粒子共同运动,寻找合适的pbest和gbest使得核函数值K(Xi,X)最优。搜索的个体历史最优位置和所处群体的历史最优位置在pbest=9.9608,gbest=0.9893,将最优参数用于构建识别器,识别效果如图11所示,其中蓝色‘o’点是样本标签类别,红色‘*’点是识别器输出结果。

由图11可知,识别效果达到100%,使用非线性变换后1.5维谱的方法是可以区分这三类实测舰船的。该方法在实测信号的应用结果证明了其实用性。

图11 实测舰船信号识别结果图

5 结论

综上述实验仿真可得结论：对于Alpha稳定分布噪声环境下的舰船辐射噪声,反正切非线性变换可以有效地抑制噪声影响,从而适用于二阶次或高阶次的信号处理方法。非线性变换后功率谱和1.5维谱都可以有效恢复舰船辐射噪声频域特征,为识别提供依据。对舰船辐射噪声仿真信号和实测信号都取得了良好的效果,实现了Alpha稳定分布噪声环境下舰船识别的要求。

[1] Pan Yue, Zhao Anbang, Li Jiangqiao, et al. Ship Radiated Noise Modulation Feature Extraction Based on CEEMD and Wavelet Threshold Noise Reduction[C]∥International Industrial Informatics and Computer Engineering Conference,2015:1763-1766.

[2] Li Yuxin, Li Yaan, Chen Zhe, et al. Feature Extraction of Ship-Radiated Noise Based on Permutation Entropy of the Intrinsic Mode Function with the Highest Energy[J]. Entropy, 2016, 18(11):393-397.

[3] Mu Lin, Peng Yuan, Qiu Mengran, et al. Study on modulation spectrum feature extraction of ship radiated noise based on auditory model[C]∥Ocean Acoustics (COA), 2016 IEEE/OES China. IEEE, 2016:82- 86.

[4] Wang Yichuan, Li Haitao, Dai Weiguo. Application of Duffng Oscillator in Ship Propeller Blade Number recognition[C]∥Ocean Acoustics (COA), 2016 IEEE/OES China. IEEE, 2016: 15-20.

[5] Chitre M, Potter J, Heng O S. Underwater acoustic channel characterisation for medium-range shallow water communications[M].OCEAN’S 04.MTTS/IEEE TECHNO-OCEAN’04, 2004:34- 40.

[6] Zhang Anqing, Qiu Tianshuang,Zhang Xinhua. A New Underwater Acoustic Signals Processing Approach to α-Stable Distribution[J].Jounal of Electronics & Information Technology,2005,27(8):1201-1203.

[7] Li Qin, Yuan Bingcheng, Ming Xing. Simulation Technique of Radiated Noise from Underwater Target and Its Implement of Simulator[C]∥Second International Conference on Power Electronics and Intelligent Transportation System,2009:357-360.

[8] Zhou Yali, Zhang Qizhi, Yin Yixin. Active control of impulsive noise with symmetric α-stable distribution based on an improved step-size normalized adaptive algorithm[J]. Mechanical Systems & Signal Processing, 2014, 56(5):320-339.

[9] Jiang Jinglong, Zha Daifeng. Generalized Fractional Lower-order Spectrum of Alpha Stable Distribution Process[C]∥Forth International Conference on Wireless Communications, Networking and Mobile Computing, 2008: 1- 4.

[10]樊养余, 孙进才. 舰船噪声的3/ 2维谱特征提取[J]. 声学学报, 2002(1):71-76.

Fan Yangyu, Sun Jincai. Feature extraction of ship radiated noise by 3/ 2 spectrum[J]. Acta Acustica, 2002(1):71-76. (in Chinese)

[11]Yin Yumei, Cui Hongyu, Hong Ming, et al. Prediction of the vertical vibration of ship hull based on grey relational analysis and SVM method[J]. Journal of Marine Science and Technology, 2015, 20(3):467- 473.

[12]Sun Li, Wang Deyu. Optimal Structural Design of the Midship of a VLCC Based on the Strategy Integrating SVM and GA[J]. Journal of Marine Science and Application, 2012,11(1):59- 67.

[13]刘逸. 粒子群优化算法的改进及应用研究[D]. 西安：西安电子科技大学, 2012:26- 40.

Liu Yi. Improvements and Applications of Particle Swarm Optimization Algorithm[D]. Xi’an: Xi’an Electronic and Engineering University, 2012:26- 40.(in Chinese)