聚焦的子空间正交性测试宽带DOA估计方法

蔡 进 刘春生 陈明建 周青松

(国防科技大学电子对抗学院,安徽合肥 230037)

1 引言

对信号源来波方向进行估计是雷达等探测系统的基本任务之一。目前,窄带信号阵列DOA估计算法已经发展的很成熟,常用的有这三类：基于子空间分解的多信号分类法(Multiple Signal Classification, MUSIC)[1]、旋转子空间不变法(Estimation of Signal Parameters via Rotation Invariance Techniques, ESPRIT)[2-3]和子空间拟合法[4-5]。随着宽带信号的应用范围更加广泛,对宽带信号的DOA估计成为这个领域研究的热点内容[6]。

目前对宽带信号进行DOA估计主要方法是：首先将时域模型通过DFT转化为频域模型,然后在频域上采用窄带信号处理的方法。针对宽带信号的DOA估计信号子空间算法(Signal Subspace Method,SSM)主要分为两类：一类是非相干子空间法(Incoherent Signal Subspace Method,ISSM)[7]。ISSM是在宽带信号中的多个频点上使用MUSIC等算法,然后对各个频点的DOA结果做平均处理,获得最终DOA估计结果。因为各个频率点的能量分布不均匀,ISSM 算法在某些频率点的估计误差较大,因此该算法要求信噪比更高并且样本数足够；另一类是相干子空间处理法(Coherent Signal Subspace Method, CSSM)[8]。该算法利用了聚焦的思想,能提高低信噪比条件下的估计精度,并且能够处理宽带相干信源。该方法缺点是在构造聚焦矩阵时,首先得对角度进行合理预估计并且要选择合适的聚焦频点,不合理的角度预估计会带来较大的DOA估计误差[9]。针对该问题,Yoon等人提出了一种投影子空间正交性测试(Test of Orthogonality of Projected Subspaces, TOPS)算法[10],该算法不用构造聚焦矩阵和角度预估计,估计精度介于ISSM法与CSSM法之间。但该算法的性能依赖参考频点的选择,并且十分容易产生伪峰；文献[11]提出了一种改进的ETOPS算法,该算法从信号带宽内的所有频率中选择几个频率点形成参考频率集,在每个频率上采用TOPS算法,虽然克服了对参考频点的依赖,但同时带来了计算的复杂度,并且不能消除伪峰。文献[12]提出了TOFS算法,利用各个频点的阵列方向矢量与噪声子空间的正交性完成DOA估计,算法不依赖参考频点,且能消除伪峰,其本质上是一种基于ISSM算法扩展的算法,因此,在中等信噪比时算法性能不太理想。

为改进传统TOPS算法存在的不足,本文提出一种聚焦的FTOPS算法。该算法是先利用RCM(Reduced Covariance Matrix)[13]法消除了噪声,然后将各个频点的Signal Subspace聚焦到任意参考频点的Signal Subspace,最后利用该参考频点的Signal Subspace与阵列方向矢量的正交投影矩阵之间的正交性完成DOA估计。仿真验证了该方法不依赖参考频点的选择,有效地消除了伪峰,角度分辨力和检测精度更高。

2 宽带信号模型

(1)

式中,xm(t)为第m个阵元上的接收信号,si(t)为第i个信号,nm(t)为第m个阵元上的复圆高斯空时白噪声。

将接收数据分成L段,对每段数据做离散时间傅里叶变换,并将宽带信号频域分成J个子带,得到频率fj,j=1,2,…,J处的频域数学模型：

(2)

将上式扩展成M个阵元,得到矩阵形式的频域阵列信号接收模型：

X(fj)=A(fj,θ)S(fj)+N(fj)j=1,2,…,J

(3)

式中,X(fj)=[x1(fj),x2(fj),…,xM(fj)]T为M×1的阵元接收信号矢量,A(fj,θ)=[a(fj,θ1),a(fj,θ2),…,a(fj,θP)]为M×P的阵列流型矩阵,入射信号矢量为s(fj)=[s1(fj),s2(fj),…,sP(fj)]T,N(fj)表示阵列噪声矢量。a(fj,θi)表示信号的方向矢量,可表示为：

a(fj,θi)=[1,exp(jφji),exp(j2φji),…,

exp(j(M-1)φji)]T

(4)

假设信号和噪声之间的相关系数为零,则可以列出频域阵列接收信号协方差矩阵为：

Rx(fj)=E{X(fj)XH(fj)}=

A(fj,θ)Rs(fj)AH(fj,θ)+Q(fj)

(5)

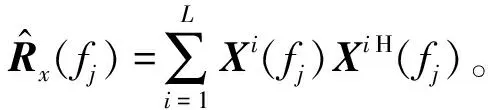
(6)

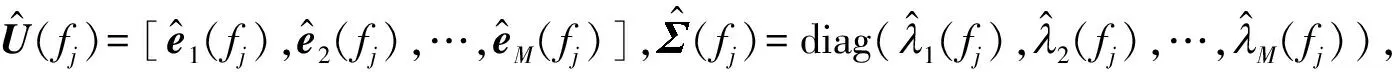
(7)

(8)

3 基于聚焦TOPS算法宽带信号DOA估计

3.1 传统的TOPS算法

TOPS算法的核心思想是将各个频点的噪声子空间(Noise Subspace)投影到由参考频点Signal Subspace生成的对应的各个频点的Signal Subspace上。这些投影形成一个构造矩阵,对构造矩阵进行角度搜索,当搜索角度等于DOA时构造矩阵将缺秩,利用该特性来估计DOA。

引理1给定ULA的方向矢量a(fp,θp)和对角变换矩阵φ(fq,θq),两者的乘积是一个新的方向矢量a(fk,θk),即：

a(fk,θk)=φ(fq,θq)a(fp,θp)

(9)

其中,fk=fp+fq,sinθk=(fp/fk)sinθp+(fq/fk)sinθq,φ(fq,θq)是M×M维对角阵,第m个对角元素为[φ(fq,θq)]m×m=exp[-j2πfq(m-1)dsinθq/c]。当θq=θp时,有θk=θp。因此,方向矢量在不改变方向的条件下,频率可由fp变成fk。

引理2假定Δfj=fj-fr,文献[10]证明了下列两个矩阵的列空间是相同的,即：

(10)

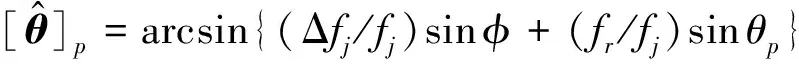
p=1,…,P

(11)

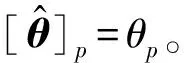
利用引理1和引理2可得出如下结论：

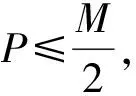
U(fj,φ)=φ(Δfj,φ)Us(fr)j=1,…,J且j≠r

(12)

其中,Δfj=fj-fr,φ是可能到达角。定义P×(J-1)(M-P)矩阵D(φ)为

(13)

文献[10]已经证明：当假定角度φ=θp,p=1,…,P时,矩阵D(φ)将缺秩；反之,当假定角度φ≠θp,p=1,…,P时,矩阵D(φ)将行满秩。对D(φ)做奇异值分解,找到最小奇异值σmin(φ),通过对(14)进行谱峰搜索可得到DOA估计值：

(14)

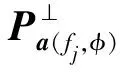
(15)

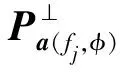
(16)

用U′(fj,φ)代替U(fj,φ)构造新的D(φ)矩阵,利用(14)进行谱峰搜索估计得到DOA。

3.2 基于聚焦的FTOPS算法

分析TOPS算法可知,因为某些参考频点的Signal Subspace可能存在较大的误差,则经过对角变换后,其误差会扩散到各个频点的信号子空间中去,因此算法十分依赖参考频点的选择。Signal Subspace和Noise Subspace必然都存在误差,后面会证明两者误差的相互作用才是产生伪峰的根本原因,尤其在信噪比较低或者快拍数不够的情况下,两者的误差会更大,因此伪峰会更加明显。

针对TOPS算法存在的问题,本文提出聚焦的FTOPS算法,该方法首先利用RCM法消除了噪声,然后通过变换矩阵将各个频点的Signal Subspace聚焦到参考频点的Signal Subspace,最后利用参考频点的Signal Subspace与阵列方向矢量的正交投影矩阵之间的正交性完成DOA估计。

1. RCM法去噪

(17)

其中,D{}表示返回一个对角矩阵,它包含了被作用矩阵对象的对角线上的元素,由(17)可知：

APAH-D{APAH}

(18)

可见通过矩阵对消作用,噪声协方差矩阵Q被消除了,对其进行特征分解：

(19)

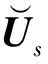
2. 剔除伪峰

Uj(fr,φ)=φ(Δfj,φ)Us(fj)j=1,…,J

(20)

其中,fr为任意参考频点,Δfj=fr-fj。通过(20),可将各个频率点的Signal SubspaceUs(fj)变换到频点fr的矩阵Uj(fr,φ)上,并且不改变其信号的DOA信息。

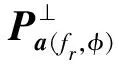
(21)

(22)

可以证明,当假定角度φ=θp,p=1,…,P时,矩阵Dj(φ)将行缺秩；反之,当假定角度φ≠θp,p=1,…,P时,矩阵Dj(φ)将行满秩。证明如下：

(23)

若φ=θp,p=1,…,P,则：

故而,证明了Dj(φ)行缺秩。

将各个频点构造矩阵Dj(φ)求和得到聚焦矩阵D(φ)：

(24)

对D(φ)做奇异值分解,找到最小奇异值σmin(φ),通过对(24)进行谱峰搜索可得到DOA估计值：

(25)

3. 剔除伪峰的证明

(1)TOPS算法存在伪峰的原因

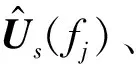
(26)

(27)

由于ΔUs(fj)必然落在Noise Subspace内,而ΔUn(fj)必然落在Signal Subspace内,故而存在(M-P)×P矩阵B和P×(M-P)矩阵C使得：

ΔUs(fj)=Un(fj)B

(28)

ΔUn(fj)=Us(fj)C

(29)

现在试着在Noise Subspace中找到一组向量满足式(4)的形式,假设存在该向量为：

a(fj,θk)=[1,exp(jφjk),exp(j2φjk),…,

exp(j(M-1)φjk)]T

(30)

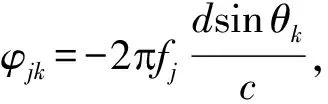
aT(fj,θk)a(fj,θi)=0

(31)

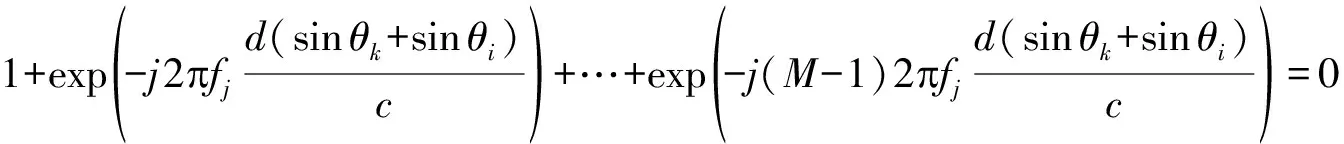
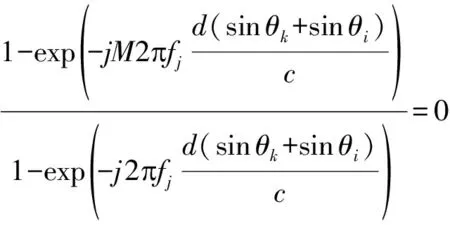
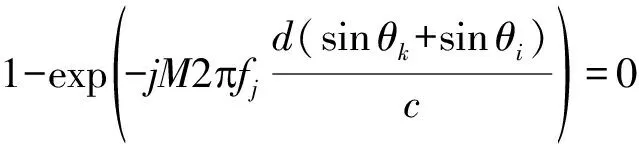
(32)

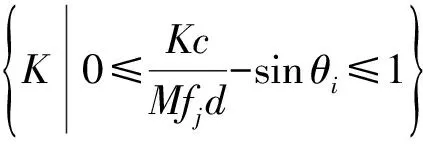
将这样的向量a(fj,θk)组成矩阵A⊥(fj,θ′),则近似有A⊥(fj,θ)∈span{Un(fr)}。由引理2可知：

j=1,…,J

(33)

k=1,2,…

(34)

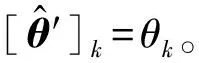
故而,利用引理1和引理2可知,存在M×P矩阵U⊥(fj,φ)

U⊥(fj,φ)=φ(Δfj,φ)ΔUs(fr)j=1,…,J且j≠r

(35)

其中,Δfj=fj-fr,φ是可能到达角。同样定义P×(J-1)(M-P)矩阵D′(φ)为

D′(φ)=[U⊥(f1,φ)HΔUn(f1)|U⊥(f2,φ)HΔUn(f2)|…

|U⊥(fJ,φ)HΔUn(fJ)]

(36)

当φ=θk,p=1,2,…时,D′(φ)将缺秩。这也就证明了当搜索角度φ不等于波达角时,也会存在谱峰。

(2)FTOPS算法剔除伪峰的原因

4. 算法复杂度分析

文献[14]证明了对一个M×M维的矩阵做SVD分解,算法复杂度大约在O(M3)。因此传统的TOPS算法在每个搜索角度对维度P×(J-1)(M-P)构造矩阵D(φ)进行奇异值分解,每个搜索角度下的SVD分解的算法复杂度略大于O(P3)(因为(J-1)(M-P)>P,包含更多的矩阵乘法运算)。本文提出的FTOPS算法是对P×M维的聚焦矩阵D(φ)做SVD分解,故而算法复杂度的量级依然是O(P3),但由于M<(J-1)(M-P),故而算法复杂度要小于传统的TOPS算法。而文献[11]提出的ETOPS算法,需要在多个频点上采用TOPS算法,故而算法复杂度为KO(P3)。综上所述,三种算法复杂度满足以下关系：ETOPS>TOPS>FTOPS。

综上所述,本文算法步骤简述如下：

(1)对阵元接收到的宽带信号总的快拍数目进行分段,对每段快拍数进行离散傅里叶变换；

(2)求出各个频点处的协方差矩阵Rx(fj)；

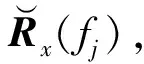
(5)对聚焦矩阵D(φ)进行奇异值分解,利用(25)进行谱峰搜索,得到P个极大值点,对应的即为信号来波方向。

4 仿真实验与分析

为检验本文提出的FTOPS算法的有效性,对本文算法和传统TOPS算法以及文献[11]提出的ETOPS算法、文献[12]提出的TOFS算法进行仿真对比。基本仿真条件：阵元数为10的均匀线阵列,阵元间距为中心频率对应的半波长,假设空间有两个远场独立宽带信号源,信号方向分别为(30°,33°),信号中心频率为300 MHz,信号带宽为B=100 MHz,采样频率为fs=700 MHz,阵列输出信号的DFT的点数为256,每个频点快拍数为132,每个条件下进行1000次蒙特卡罗仿真实验。

由仿真1可知：(1)传统TOPS算法以及ETOPS算法无论在低信噪比还是中等信噪比都会出现多个伪峰,在低信噪比时,估计分辨力较差；(2)ETOPS算法性能要优于在该参考频点下的传统TOPS算法；(3)本文提出的FTOPS算法和TOFS算法都能够有效剔除伪峰,但是本文算法谱峰更尖锐,在低信噪比条件下分辨力更高。

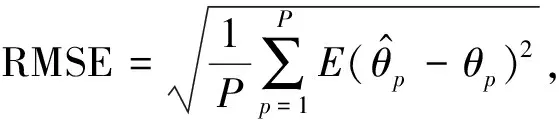
图1 不同信噪比时的空间谱

图2 不同信噪比算法的均方根误差

图3 不同角度间隔算法的成功估计概率

由仿真2可知：(1)四种方法的均方误差随着信噪比的提高而减少；(2)ETOPS算法的均方误差要小于传统TOPS算法；(3)TOFS算法均方误差曲线最高,尤其在中等信噪比和低信噪比下表现更差；(4)在整个信噪比区间上,FTOPS算法的均方误差都小于另外三种算法。

由仿真3可知,在5 dB的仿真条件下,四种方法的成功估计概率,随着角度间隔的增大而提高；当角度间隔小于等于1°时,四种算法都无法分辨开信号；在角度间隔1.5°时,传统TOPS算法、ETOPS算法以及TOFS算法几乎无法正确估计,而FTOPS算法成功估计的概率超过了0.5；当角度间隔为2°时,FTOPS算法成功估计概率为1,而传统ETOPS算法仅有0.4。说明本文算法在低信噪比下具有更高的分辨力。

仿真分析,因为传统TOPS算法采用由参考频点生成的Signal Subspace与各个频点的Noise Subspace的正交性完成DOA估计,而参考频点的Signal Subspace的误差会扩散到各个频点的Signal Subspace中,故而参考频点的选择非常重要,其次,Signal Subspace的误差和Noise Subspace的误差的相互作用会产生伪峰；ETOPS算法通过选取一个频率集,在这个频率集上采用TOPS算法,因此能减少算法对参考频点的依赖,性能上要优于TOPS算法；而TOFS算法虽然能够克服对参考频点的依赖,且消除了伪峰,但本质上还是ISSM算法的扩展,因此在中等信噪比和低信噪比下表现不佳。

本文提出的FTOPS算法是利用转换矩阵把各个频点的Signal Subspace聚焦到任意参考频点的Signal Subspace,最后利用该参考频点的Signal Subspace与阵列方向矢量的正交投影矩阵之间的正交性完成DOA估计。由于利用到了各个频点的Signal Subspace信息,故而算法不依赖参考频点的选择；其次用阵列方向矢量的正交投影矩阵代替Noise Subspace,没有了Noise Subspace的误差,故而能剔除伪峰。同时,利用RCM法进行去噪预处理,提高了在低信噪比条件下算法的估计精度。

5 结论

本文采用聚焦的思想,提出了基于聚焦的FTOPS算法,将各个频点的Signal Subspace聚焦到任意参考频点的Signal Subspace,最后利用该参考频点的Signal Subspace与阵列方向矢量的正交投影矩阵之间的正交性完成DOA估计,并利用RCM法去噪,提高了在低信噪比条件下的估计精度,解决了TOPS算法性能依赖参考频点选择、存在伪峰等问题。同时理论上推导证明了TOPS算法存在伪峰和FTOPS算法能剔除伪峰的原因。仿真证明了,在低信噪比条件下,相对TOPS算法,本文算法参数估计精度和角度分辨率更高。

[1] Qian C, Huang L, So H C. Improved Unitary Root-MUSIC for DOA Estimation Based on Pseudo-Noise Resampling[J]. IEEE Signal Processing Letters, 2014, 21(2):140-144.

[2] Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1990, 37(7):984-995.

[3] Chen C, Zhang X. A RD-ESPRIT algorithm for coherent DOA estimation in monostatic MIMO radar using a single pulse[J]. International Journal of Electronics, 2014, 101(8):1074-1085.

[4] Viberg M, Ottersten B. Sensor array processing based on subspace fitting[J]. IEEE Transactions on Signal Processing, 1991, 39(5):1110-1121.

[5] 孙磊, 王华力, 熊林林,等. 基于贝叶斯压缩感知的子空间拟合DOA估计方法[J]. 信号处理, 2012, 28(6):827- 833.

Sun Lei, Wang Huali, Xiong Linlin, et al. A Novel Subspace Fitting Method for DOA Estimation Based on Bayesian Compressive Sensing[J]. Signal Processing, 2012,28(6):827- 833. (in Chinese)

[6] Garmatyuk D S, Narayanan R M. ECCM capabilities of an ultrawideband bandlimited random noise imaging radar[J]. IEEE Transactions on Aerospace & Electronic Systems, 2002, 38(4):1243-1255.

[7] Wax M, Shan T J, Kailath T. Spatio-temporal spectral analysis by eigenstructure methods[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1984, 32(4):817- 827.

[8] Wang H, Kaveh M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1985, 33(4):823- 831.

[9] Sellone F. Robust auto-focusing wideband DOA estimation[J]. Signal Processing, 2006, 86(1):17-37.

[10]Yoon Y S, Kaplan L M, Mcclellan J H. TOPS: new DOA estimator for wideband signals[J]. IEEE Transactions on Signal Processing, 2006, 54(6):1977-1989.

[11]Zhang J, Dai J, Ye Z. An extended TOPS algorithm based on incoherent signal subspace method[J]. Signal Processing, 2010, 90(12):3317-3324.

[12]Yu H Q, Huang Z T, Liu J, et al. TOFS: A new DOA estimator for wideband sources[J]. Journal of Astronautics, 2007.

[13]Liao B, Huang L, Guo C, et al. New Approaches to Direction-of-Arrival Estimation With Sensor Arrays in Unknown Nonuniform Noise[J]. IEEE Sensors Journal, 2016, 16(99):1-1.

[14]Golub G H, Van Loan C F. Matrix computations[J]. Mathematical Gazette, 1996, 47(5 Series II):392-396.