MIMO雷达迭代最差性能最优鲁棒波束形成算法

谭志浩 金 伟 贾维敏

(火箭军工程大学,陕西西安 710025)

1 引言

多输入多输出(Multiple Input Multiple Output, MIMO)雷达[1],可以利用发射天线发射正交波形提高系统的自由度,从而获得很好的目标分辨能力和干扰抑制能力。波束形成是MIMO雷达领域的重要研究方面。MIMO雷达输出信号模型与相控阵雷达具有相同的形式,因此可以直接将自适应波束形成算法应用于MIMO雷达中。

自适应波束形成算法一般可分为四类[2]：对角加载类算法,特征空间类算法,协方差重构类算法和不确定集类算法。对角加载类算法[3]可以通过部分加载的方式保证很好的鲁棒性,但最优加载量的选取却难以确定。特征空间类算法[4],低信噪比条件下信号成分与噪声成分的“缠绕”现象亟待解决。对于MIMO雷达来说,协方差矩阵维数为发射阵元数和接收阵元数之积,其维数往往较高。协方差重构类算法[5-7],要保证估计的协方差矩阵足够准确,需要更多的训练样本和很高的计算复杂度,不利于实际的工程应用。不确定集类算法[8-9],当估计的导向矢量与真实的导向矢量无失配误差时,可以保证很好的性能。文献[8]提出的基于最差性能最优(Worst-case, WC)算法和文献[9]提出的基于不确定集的导向矢量估计(Robust Capon Beamforming, RCB)算法,是最经典的自适应波束形成算法。为了获得更准确的目标导向矢量,大量改进的不确定类算法被提出[10-12]。最差情形一般以较小的概率出现,文献[10]提出基于概率约束对WC算法进行一定的改进。文献[11]和文献[12]提出利用较小的不确定集来约束误差,通过迭代不断更新假定导向矢量,从而获得更准确的导向矢量。针对MIMO雷达收发两端的结构特点,文献[13]提出双迭代的方法分别获得发射和接收导向矢量。文献[14]在文献[13]的基础上,提出利用整体线性联合方法估计协方差矩阵,并结合目标角域范围对误差约束集进行改进,将假定导向矢量和真实导向矢量之间的失配量约束在假定导向矢量正交补空间中。

本文依据MIMO雷达阵列结构,对联合导向矢量失配误差,尤其是方向误差进行了理论推导,给出了集中式MIMO雷达方向估计误差的收敛经验值,并基于此对大不确定集算法的局限性进行分析。针对联合导向矢量初始假定值和真实值失配较大的情况,在文献[12]的基础上,提出基于小不确定集的MIMO雷达迭代最差性能最优波束形成算法,首先基于WC算法由初始假定联合导向矢量获得较为准确的权矢量,然后利用权矢量与联合导向矢量对应关系,求解出新的假定联合导向矢量,通过不断迭代更新假定值,最终获得更准确的联合导向矢量,从而提升MIMO雷达系统性能。

2 MIMO雷达基本模型

假设MIMO雷达系统是阵元间隔为半波长的均匀线阵,发射和接收阵元数分别为M和N。研究对象一般为远场点目标,目标信号的波离角为θt,波达角均为θr。则发射和接收导向矢量可分别表示为：

at=[1,ejπsin(θt),…,ejπ(M-1)sin(θt)]T

ar=[1,ejπsin(θr),…,ejπ(N-1)sin(θr)]T

(1)

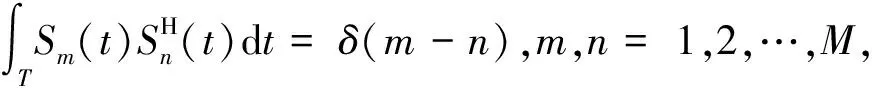
S(t)=[S1(t),S2(t),...,SM(t)]T

(2)

其中,t为发射信号在周期内的某一时刻,(·)T和(·)H分别表示矩阵的转置和共轭转置。

假定有K个目标,则接收到的信号可表示为：

(3)

其中,αl(τ)为散射系数,al,t和al,r分别表示第l个信号的发射和接收导向矢量,τ表示脉冲数,n(t,τ)为复高斯白噪声。这里需要说明,本文采用的雷达散射模型服从施威林II模型,即对每个目标来说,散射系数在脉冲内完全相关,脉冲间则统计独立。

接收端对N个接收阵元的接收信号进行匹配滤波,将获得的信号向量化,可表示为：

(4)

因此,获得的采样协方差矩阵可表示为：

(5)

其中,L为采样快拍个数。最终获得的输出信干噪比SINR采用一般形式,可以表示为：

(6)

其中,w为获得的权矢量,Rs和Ri+n分别表示信号协方差矩阵和干噪协方差阵。

3 MIMO雷达迭代最差性能最优算法

本节首先结合MIMO雷达的阵元结构,对联合导向矢量失配误差,尤其是方向估计误差,进行理论分析,来说明选用小不确定集的优势。然后,提出迭代更新假定联合导向矢量的方法,利用联合导向矢量和权矢量的对应关系,获得更为准确的联合导向矢量。

3.1 失配量理论分析

实际中,由于阵元幅相误差、阵元位置误差、目标角度估计误差等各类因素的存在,假定的联合导向矢量和真实的联合导向矢量之间往往存在一定的失配,真实的联合导向矢量可表示为：

a=(at+et)⊗(ar+er)=

at⊗ar+at⊗er+et⊗ar+et⊗er

(7)

其中,et和er分别表示发射导向矢量和接收导向矢量的失配量,均满足复高斯分布,且失配量满足一定的范数约束：

‖et‖≤εt

‖er‖≤εr

(8)

其中,‖·‖表示向量的欧式范数。因此,联合导向矢量失配量可表示为：

‖e‖=‖at⊗er+et⊗ar+et⊗er‖≤

‖at⊗er‖+‖et⊗ar‖+‖et⊗er‖≤

(9)

其中,ε表示联合导向矢量失配量。然而,式(9)给定的导向矢量失配量是基于发射和接收导向矢量失配量获得的。实际上,失配量ε的选取依然是盲目的。一方面,我们期望ε尽可能的大,以保证假定的导向矢量和真实导向矢量之间的失配量被包含在不确定集中；另一方面,我们期望ε尽可能的小,从而避免不确定集将无效角域包含在内,造成性能损失。因此,失配量的选取必须是适当的。

由式(1)可以获得联合导向矢量的形式：

a=[a11,a12,...,a1N,a21,a22,...,aMN]T

(10)

联合导向矢量a的元素amn满足：

amn=e-jπmsin(θt)×e-jπnsin(θr)=

e-jπ(msin(θt)+nsin(θr))=e-jβπ

(11)

其中,β=msin(θt)+nsin(θr)。一般的,各类误差对于导向矢量失配有幅度和相位两方面影响,因此联合导向矢量的元素可以表示为：

amn=e-jβπ×|γ|e-jφ=|γ|e-j(βπ+φ)

(12)

其中,γ和φ分别表示各类误差的幅度因子和相位因子。由于失配误差产生的途径较多,误差影响因子的实际分布往往较复杂。本文只针对集中式MIMO雷达的方向估计误差进行研究,用来说明选用小不确定集的优势。

对于集中式MIMO雷达,其收发端共置,因此可以认为波离角和波达角相同,即θt=θr,因此,式(11)可以获得更加简洁的形式：

(13)

其中,bmn=e-jπ(m+n),是发射和接收阵元数之和的函数,而sin(θ)是真实方向角θ的函数。因此,联合导向矢量方向误差失配量满足以下形式：

(14)

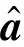
(15)

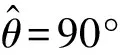
(16)

假定κ=e-jπsin(θ),则失配量的部分表达式可以分解为三部分,从而进一步转化为

-2N(-κ)N-1-2N(-κ)N+…+

6(-κ)M-2+4(-κ)M-1+2(-κ)M=

-2κ0+4κ1-6κ2+ο(κ3)

(17)

其中,ο(κ3)表示变量κ的三阶无穷小。这是因为κ∈[0,1],可以用高阶无穷小来近似取值。实际上,对于阵元数较大情形下,η≪MN,因此失配量取值满足经验取值,即ε2≈2MN,即误差失配量约为虚拟阵元数的两倍。一般的,误差失配量可以近似取为

ε2≈2MN-2κ0+4κ1-6κ2

(18)

根据式(9)和式(18),大不确定集的选取必须是适当的。当不确定集选取过大时,即远远超过式(18)的约束范围,那么将会把包括干扰在内的所有误差包含在内,从而失去约束集的实际意义。当不确定集选取过小时,即远远小于式(18)的约束时,虽然可以将其他干扰方向因素排除,但不能将目标方向附近的误差失配量完全约束。当虚拟阵元数较大时,方向失配量在真实方向角附近急剧变化,中心峰值高于式(18)的经验值,而后迅速收敛。因此,当取值过小时,大不确定集只约束了估计方向角附近极小角域,导致算法在大失配条件下失效。

3.2 迭代最差性能最优波束形成算法

WC算法是经典的自适应波束形成算法,对任意误差均具有较好的鲁棒性,其目标函数可表示为：

s.t.wHa≥ε‖w‖+1

Im{wHa}=0

(19)

上述问题可以利用CVX等凸优化工具包轻松解决。需要注意的是,WC算法也是基于大不确定集。在上一小节中,以集中式MIMO雷达的方向估计误差为对象,对基于大不确定集的算法局限性进行了理论分析。显然,对于各类误差引起的失配量,大不确定集的选取都会面临类似上述方向误差的情形。因此,选用较小不确定集,可以有效地避免不确定集包含无效角域引起的性能损失。但值得注意的是,基于小不确定集依然需要考虑将所有失配量包含在选定的不确定集中。

基于大不确定集假定初始联合导向矢量不变,忽视了接收数据对联合导向矢量的信息挖掘。这也是该类算法在导向矢量估计性能受限的根本原因。文献[12]在提出一种迭代更新假定导向矢量的方法,本文将其引入到MIMO雷达中,以解决小不确定集难以约束大失配量的问题。

基于WC算法的权矢量和联合导向矢量的关系可表示为：

(20)

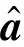
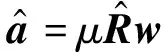
(21)

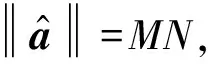
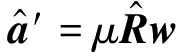
(22)

由式(22)可以获得新的联合导向矢量,用其代替初始假定的联合导向矢量,进行迭代,从而不断逼近真实的联合导向矢量,最终获得最优联合导向矢量。

实际上,迭代更新联合导向矢量的过程也是将假定联合导向矢量在角度维进行搜索的过程,通过不断移动的多个小不确定集替代原先的单个大不确定集,从而解决了小不确定集不能约束初始大失配量的情况。

3.3 迭代终止条件

对于MIMO雷达,其终止条件可以直接采用文献[11]提出的失配量与角域双约束的方式,即：

(23)

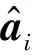
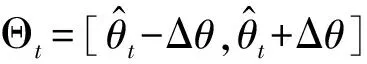
(24)

值得注意的是式(23)的第二个判别条件是为了避免估计的联合导向矢量收敛到干扰信号对应的联合导向矢量。

本文提出的MIMO雷达迭代最差性能最优算法，算法具体总结如下：

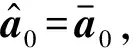
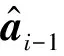
步骤3结合式(23)判断是否满足迭代终止条件,若满足,则wi即为所提算法的最优权矢量,否则,重复执行步骤2。

4 仿真结果及分析

不失一般性的,假设MIMO雷达系统为阵元间隔为半波长的均匀线阵,发射阵元数M=10,接收阵元数N=10,研究对象为远场点目标,空间存在两个干扰目标,其干噪比(Interference and Noise Ratio, INR)均为30 dB,噪声成分为标准高斯白噪声。为验证算法对于联合导向矢量大失配情形的性能,仿真实验将所提算法和文献[8]提出的WC算法、文献[9]的RCB算法、文献[13]的BIA-RCB算法以及文献[14]的BI-QCQP算法进行了性能比较。蒙德卡罗实验次数均为100次。为充分说明算法有效性,在研究集中式MIMO雷达时,仿真实验基本条件和文献[14]一致,研究分布式MIMO雷达时,仿真实验基本条件与文献[13]一致。

4.1 方向估计误差失配量实验

以集中式MIMO雷达方向误差为研究对象,假定真实目标的发射和接收角度为θt=θr=0°。图1给出了发射阵元数M=5时,不同接收阵元数条件下的方向角估计误差值变化曲线。值得指出的是,发射和接收阵元数对于方向估计误差的影响是相同的。从图1可以看出,一方面当接收阵元数一定时,随着方向角估计误差变大,其失配量逐渐收敛于一特定值,但是在临近真实方向角时,曲线变化剧烈,其峰值和谷值相差很大；一方面,失配量变化曲线随着接收阵元数增加,在真实方向角附近收敛速度更快。选用大不确定集时,当大不确定集高于峰值,此时不确定集将所有的角度均约束在内,其约束实际上无意义,即算法已经失效。当不确定集值小于峰值时,虽然能够避免将其他方向包含,但此时约束集不能完全约束失配量。换言之,大不确定集算法此时只能将真实方向角附近极小角域包含在内,显然不能适应大失配情形,这在阵元数较大情况下更为突出。本文所提算法的迭代过程等效于变化曲线在横轴方向上平移的过程。因此可以选用小不确定集,通过不断逼近,最终获得准确的联合导向矢量。

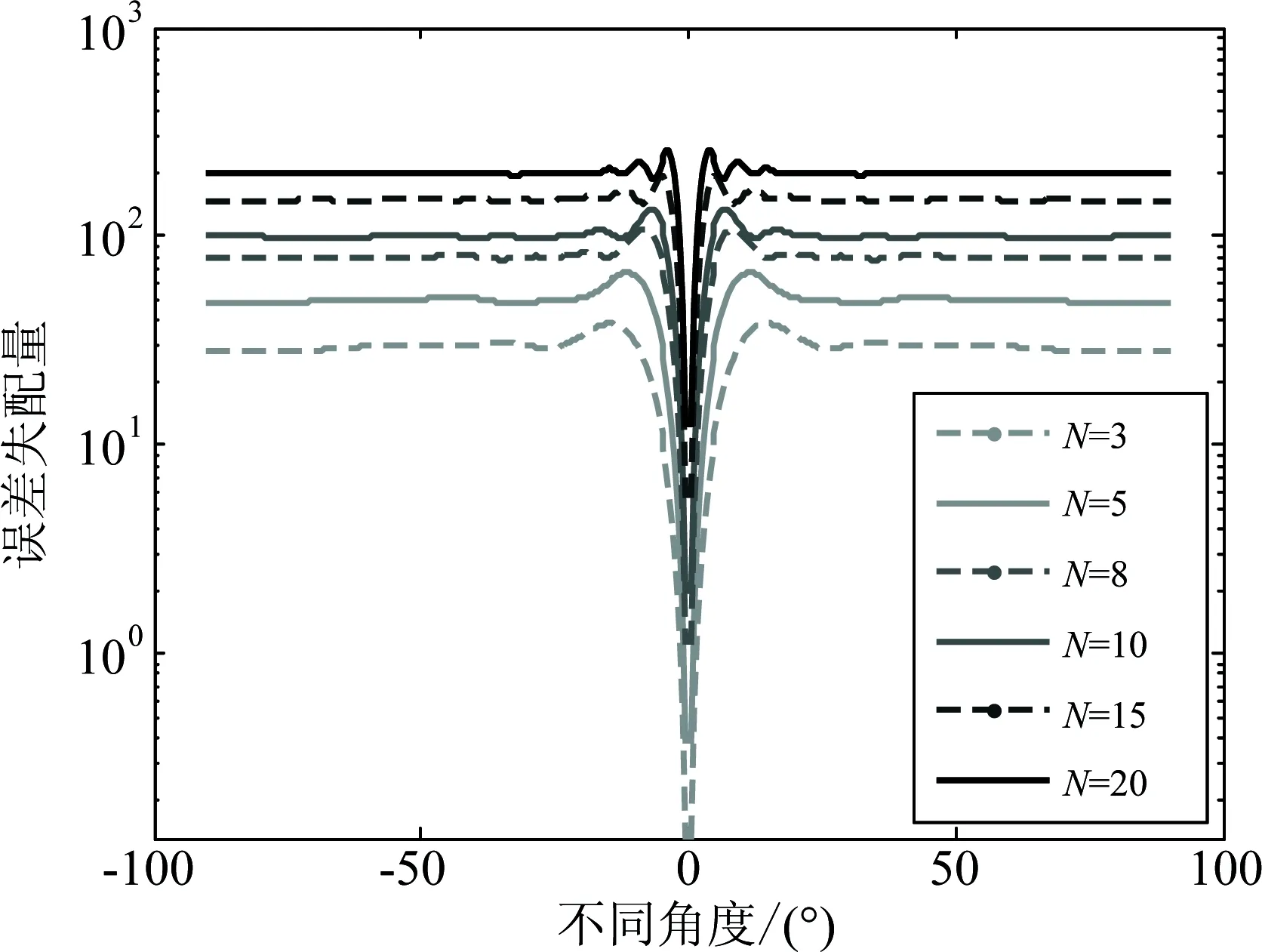
图1 不同接收阵元数下方向估计误差失配量

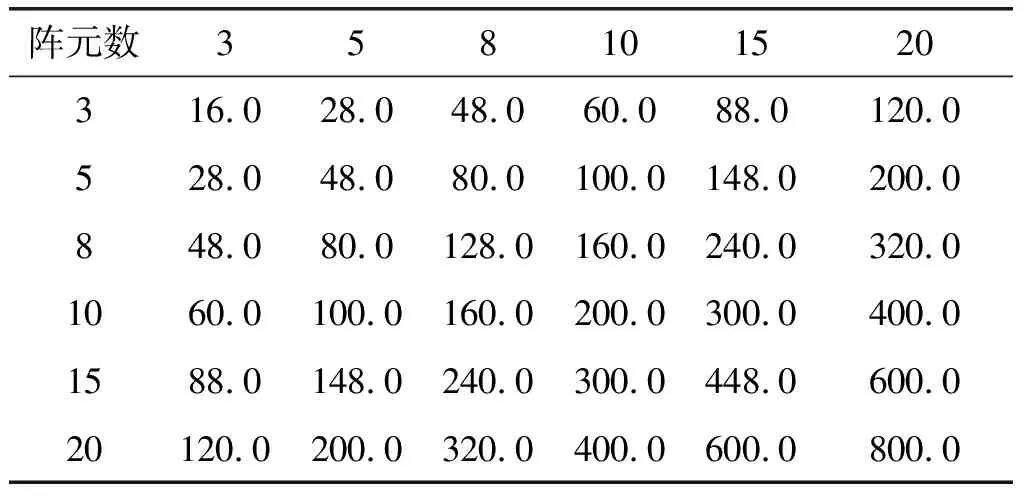
阵元数358101520316.028.048.060.088.0120.0528.048.080.0100.0148.0200.0848.080.0128.0160.0240.0320.01060.0100.0160.0200.0300.0400.01588.0148.0240.0300.0448.0600.020120.0200.0320.0400.0600.0800.0

注：表中数据形式(.0)表示保留小数点后15位取值。

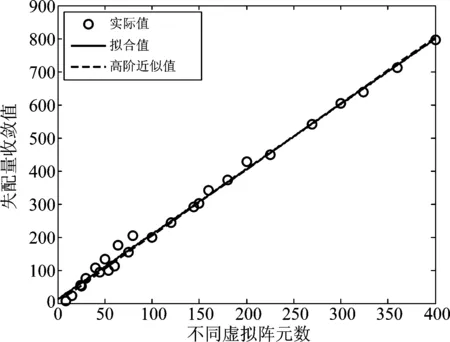
图2 不同虚拟阵元数下失配量曲线

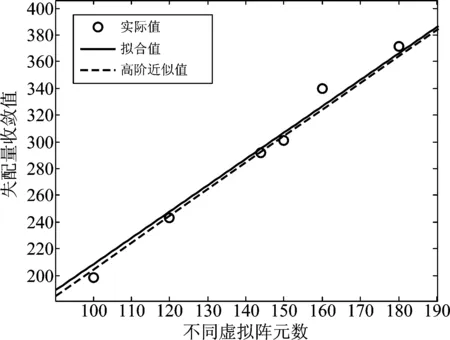
图3 不同虚拟阵元数下失配量曲线局部放大图

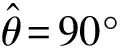
4.2 集中式MIMO雷达

集中式MIMO雷达收发共置,其发射角和接收角是一致的。假定真实的目标方向为6°,假定的目标方向为3°,方向角存在3°的失配误差,干扰方向分别为30°和50°。快拍数为L=200。各算法参数选取为：文献[8]WC算法参数ε=7,文献[9]RCB算法参数ε=8,文献[13]BIA-RCB算法参数ε=8，文献[14]BI-QCQP算法和本文所提算法的约束角度容限Δθ=5°。

图4给出了各种算法在不同信干比(Signal and Interference Ratio, SNR)条件下的输出信干噪比。从图4可以看出,所提算法对于方向角估计误差具有很好的鲁棒性,在SNR大于-20 dB时,能够获得最高的输出信干噪比性能。图5给出了SNR=-5 dB时,不同快拍的输出SINR性能。可以看出,所有算法在样本数超过200时开始收敛,而所提算法始终能保证获得最高的SINR。

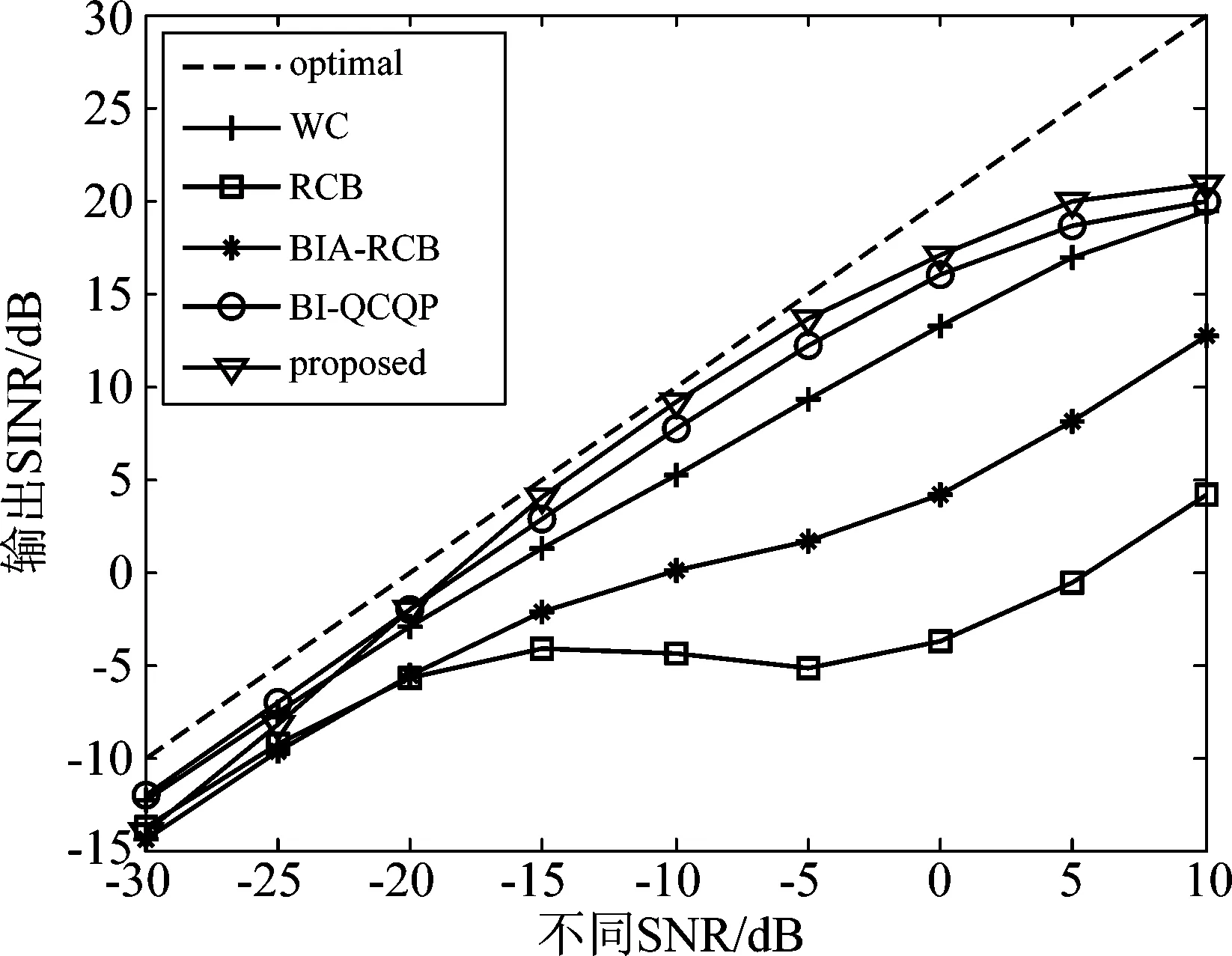
图4 不同SNR条件下的输出信干噪比

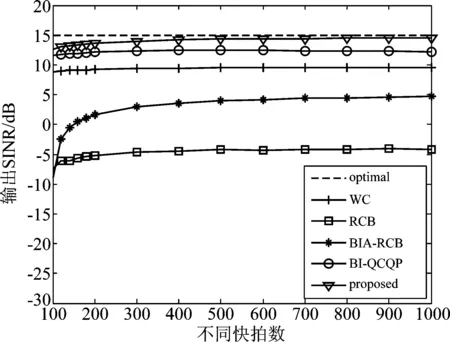
图5 不同快拍条件下的输出信干噪比

图6给出了不同的角度估计误差条件下的性能比较。可以看出,WC算法和RCB算法对于角度估计误差比较敏感,当角度估计误差较大时, SINR性能会严重下降,而本文所提算法和BIA-RCB算法、BI-QCQP算法对于方向角估计误差具有很好的鲁棒性,且本文所提算法在方向误差全角域上均能取得最高输出SINR。

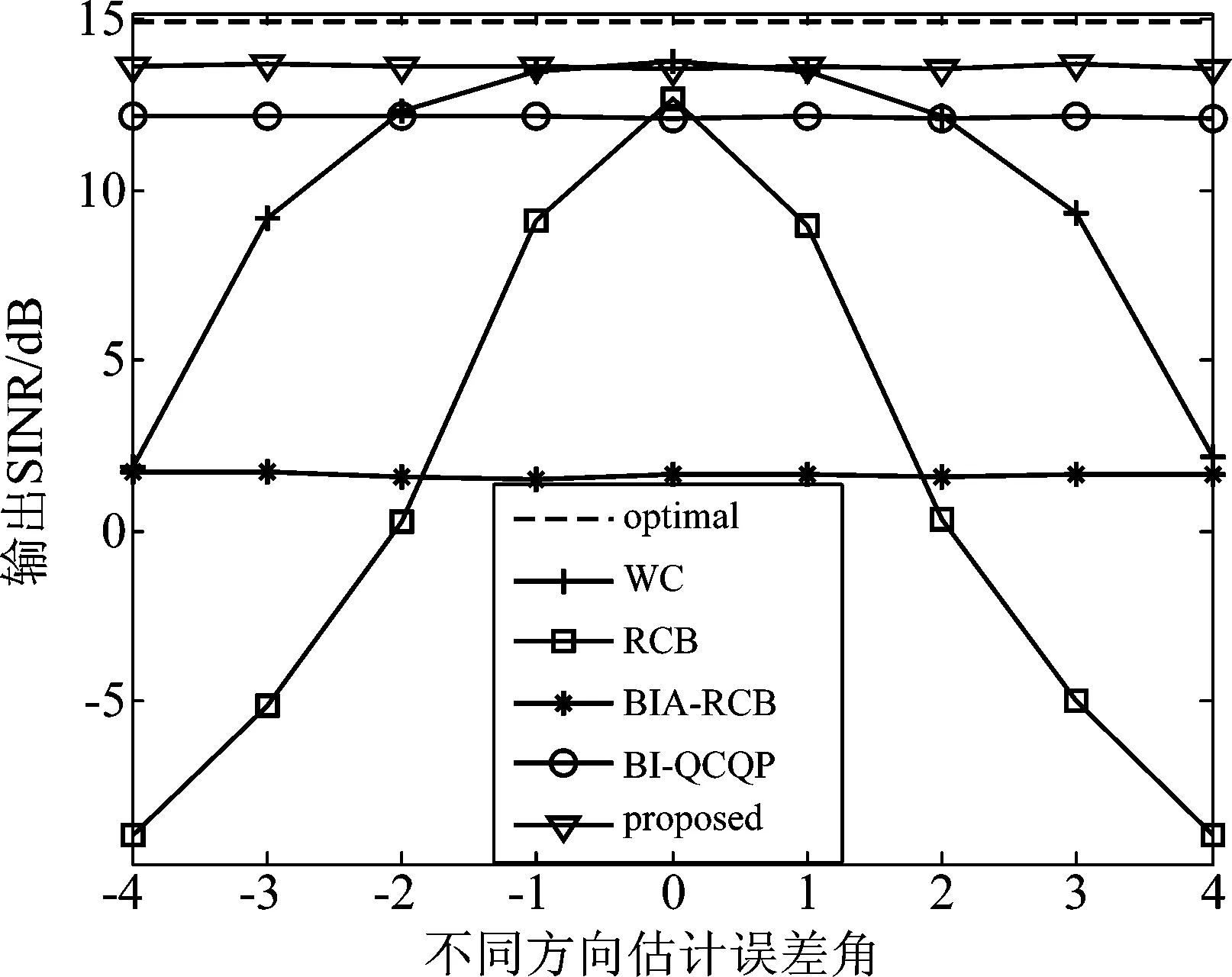
图6 不同角度估计误差条件下的输出信干噪比

图7给出了校正误差条件下的输出SINR性能。校正误差时由于阵元幅相误差及阵元位置误差产生的,因此在仿真实验中,假定发射导向矢量和接收导向矢量每个元素都受均值为0,方差为0.005的加性复高斯成分的“污染”。从图7可以看出,所提算法可以获得最高输出SINR,即算法对校正误差也具有较好的鲁棒性。

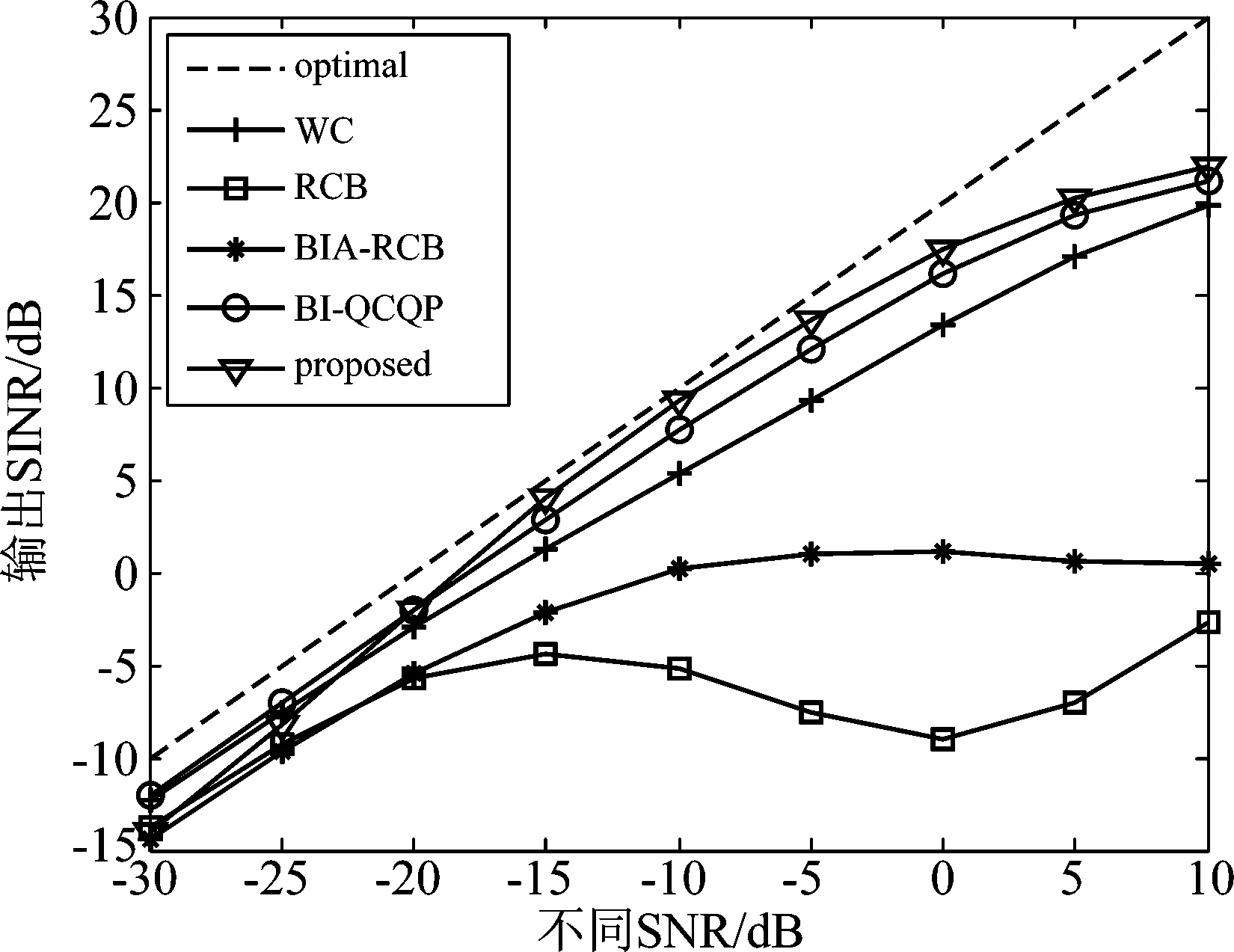
图7 校正误差条件下的输出信干噪比

图8给出了不同算法的方向图,图9是图8的局部放大图。从图中可以明显看出,本文所提算法对于方向角的估计基本与理论值相近,而BIA-RCB算法和BI-QCQP算法对于方向角估计偏差较大。换言之,本文所提算法可以获得更为准确的联合导向矢量。实际上,所提算法之所以能获得很好的输出信干噪比性能,且对于方向误差、校正误差都具有很强的鲁棒性,就是因为能获得更精确的联合导向矢量,保证权矢量更优。算法在迭代过程中不断更新假定联合导向矢量,因而可以用多个移动的小不确定集将所有失配量完全约束住。同时在真实的方位角附近时,因为采用的是较小的不确定集,与大不确定集算法相比,可以保证估计的联合导向矢量与真实的联合导向矢量的失配更小。

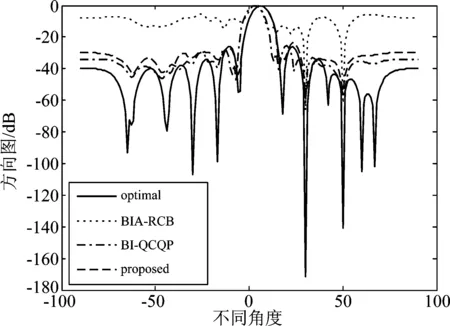
图8 不同算法的方向图

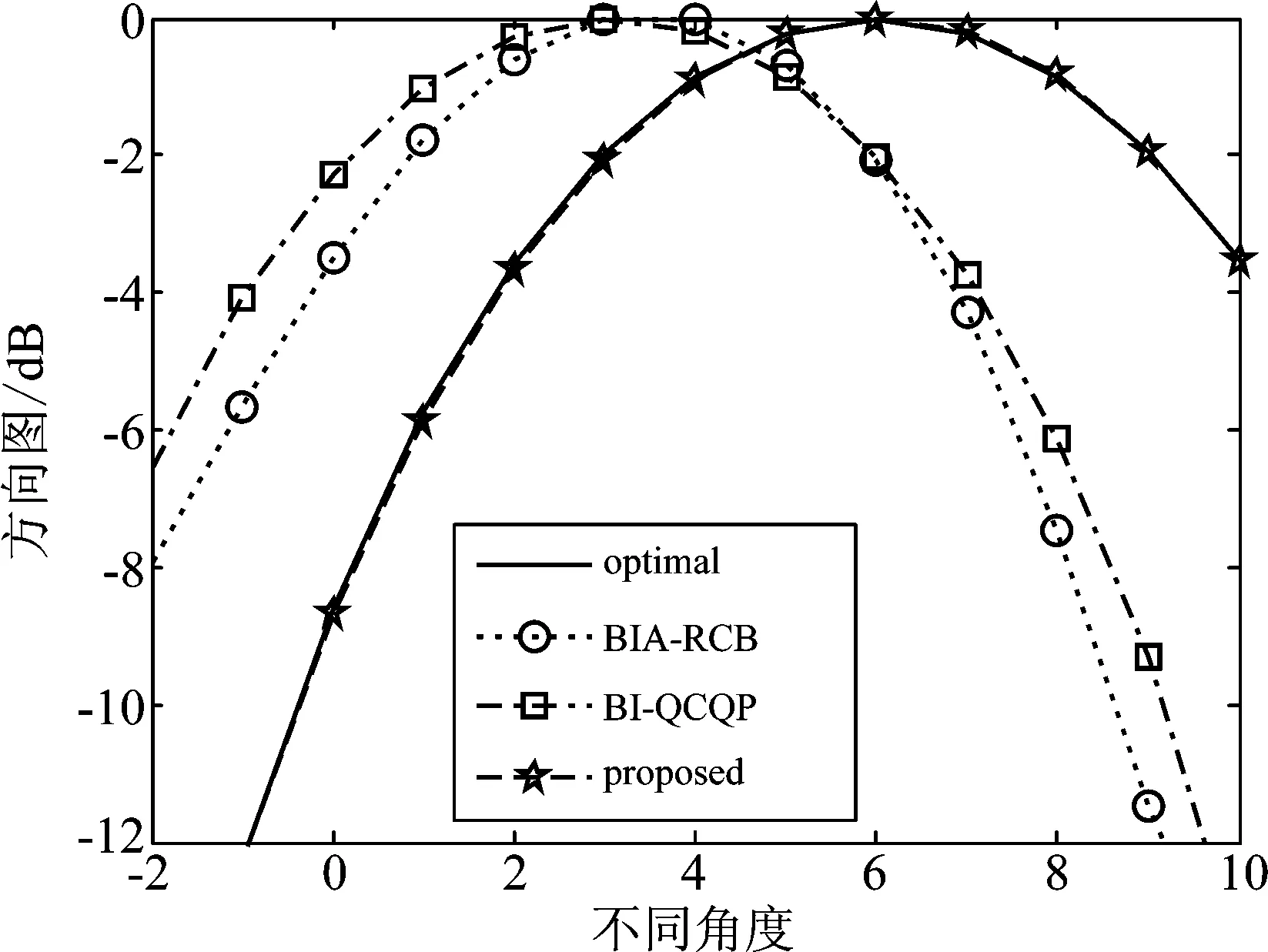
图9 不同算法的方向角估计图

4.3 分布式MIMO雷达

分布式MIMO雷达收发端分布较远,其发射角和接收角一般不同。用(θt,θr)表示波离角和波达角。仿真试验中真实的目标角为(-30°,10°),假定的目标角为(-33°,7°),方向角存在3°的失配误差,两个干扰的角度分别为(-40°,20°)和(20°,-30°)。其他仿真条件与上一小节中的集中式MIMO雷达相一致。图10给出了不同SNR条件下的输出SINR性能比较。图11给出了校正误差条件下的输出SINR性能比较。从图中可以明显看出,本文所提算法对于分布式MIMO雷达各类误差也具有很好的鲁棒性,且能获得最高的输出SINR。

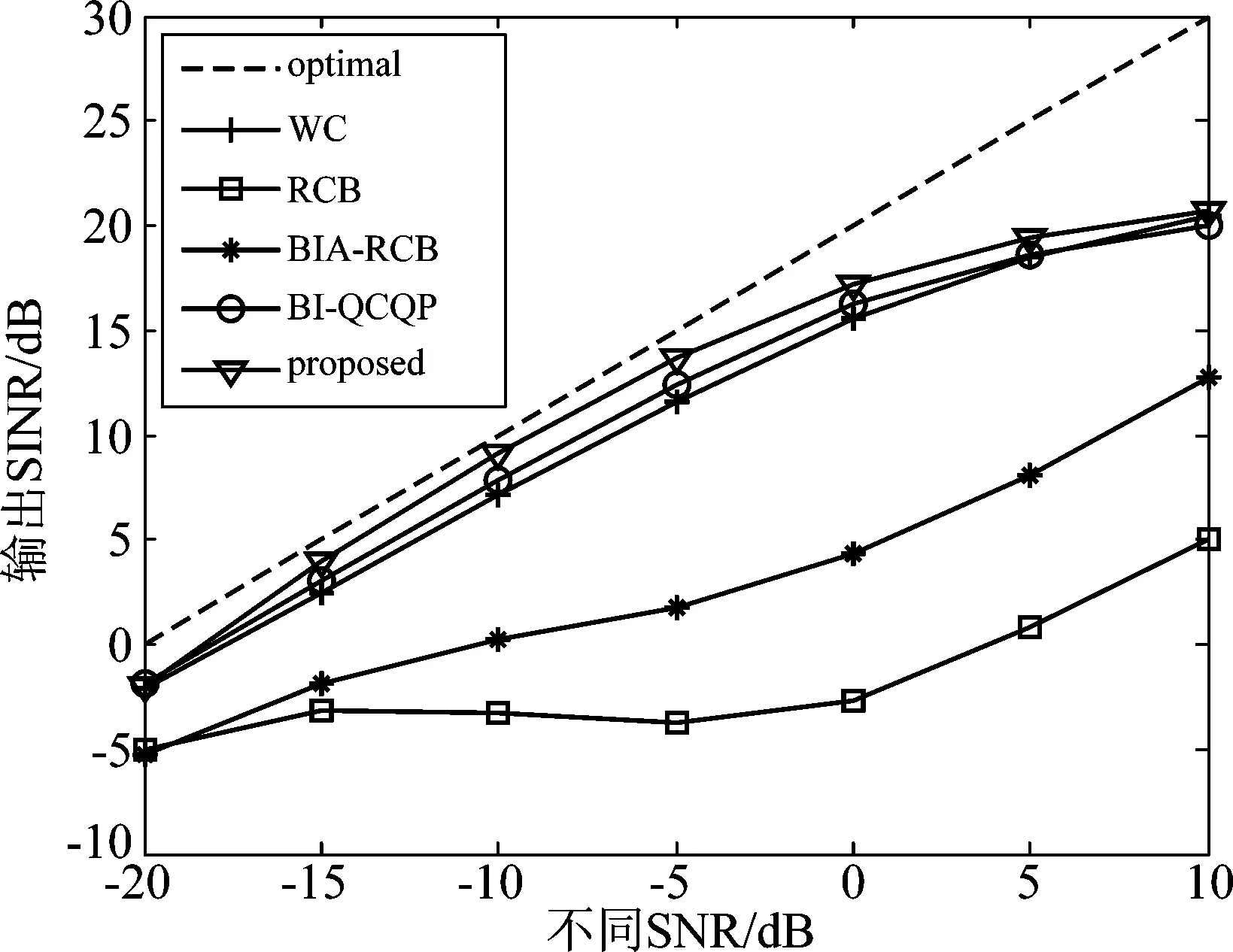
图10 不同SNR条件下的输出信干噪比

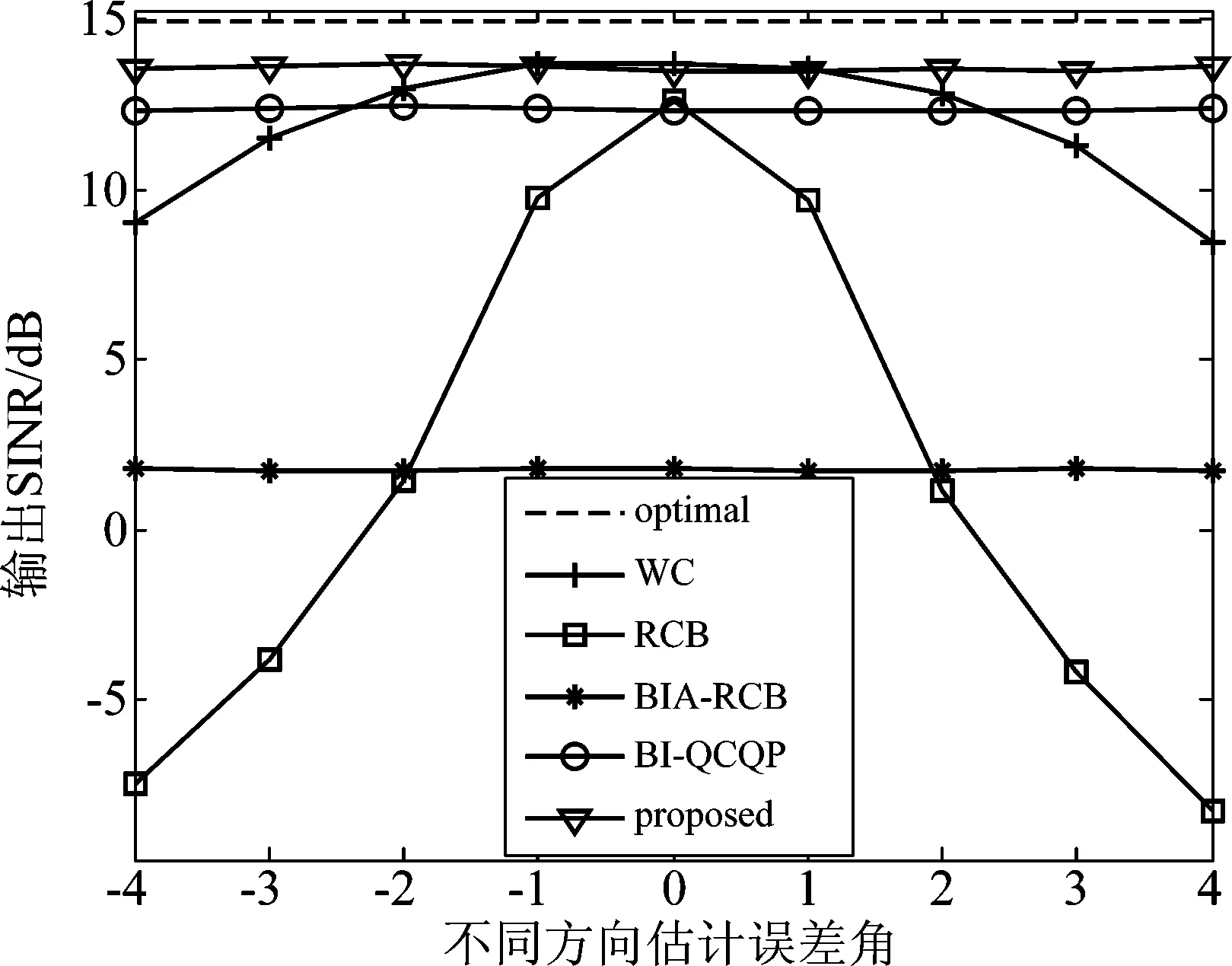
图11 不同角度估计误差条件下的输出信干噪比

5 结论

本文提出的采用小不确定集的MIMO雷达迭代最差性能最优波束形成算法,首先基于WC算法由初始假定联合导向矢量获得较为准确的权矢量,然后利用权矢量与联合导向矢量的对应关系,求解出新的假定联合导向矢量,通过不断迭代更新假定值,最终获得更准确的联合导向矢量。实验证明：所提方向估计误差经验取值与理论值相吻合,所提算法与其他算法相比,对联合导向矢量失配较大的情形下具有很强的鲁棒性,且输出信干噪比性能达到最优。

[1] Li J, Stoica P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106-114.

[2] Huang L, Zhang J, Xu Z, et al. Robust adaptive beamforming with a novel interference-plus-noise convariance matrix reconstruction method[J]. IEEE Transactions on Signal Processing, 2015, 63(7): 1643-1650.

[3] Du L, Li J, Stoica P. Fully automatic computation of diagonal loading levels for robust adaptive beamforming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 449- 458.

[4] Jia W M, Jin W, Zhou S, et al. Robust adaptive beamforming based on a new steering vector estimation algorithm[J]. IEEE Signal Processing Magazine, 2012, 93(9): 2539-2542.

[5] Gu Y, Goodman N A, Hong S, et al. Robust adaptive beamforming based on interference convariance matrix sparse reconstruction[J]. Signal Processing, 2014, 96(5): 375-381.

[6] Zhang Z, Liu W, Leng W, et al. Interference-plus-Noise convariance matri reconstruction via spatial power spectrum sampling for robust adaptive beamforming[J]. IEEE Signal Processing Letters, 2016, 23(1): 121-125.

[7] Chen P, Zhao Y, Liu C. Robust adaptive beamforming based on sparse reconstruction using a non-convex optimisation algorithm[J]. Electronics Letters, 2016, 52(19): 1584-1586.

[8] Vorobyov S A, Gershman A B, Luo Z Q. Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 313-324.

[9] Li J, Stoica P, Zhang Z S. On robust capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1702-1715.

[10]Vorobyov S A, Chen H, Gershman B. On the relationship between robust minimum variance beamformers with probabilistic and worst case distortionless response of constraints[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5719-5724.

[11]Nai S E, Ser W, Yu Z L, et al. Iterative robust minimum variance beamforming[J]. IEEE Transactions on Signal Processing, 2011, 59 (4): 1601-1611.

[12]Jin W, Jia W M, Yao M L, et al. Robust adaptive beamforming based on iterative implementation of worst-case performance optimization[J]. Electronics Letters, 2012, 48(22): 1389-1391.

[13]王勇. MIMO雷达稳健的自适应波束形成方法研究[D]. 西安: 西安电子科技大学, 2012.

Wang Yong. Study on robust adaptive beamforming for MIMO radar[D]. Xi’an: Xidian University, 2012. (in Chinese)

[14]虞泓波, 冯大政, 解虎. MIMO雷达迭代降维稳健波束形成方法[J]. 西安电子科技大学学报, 2016, 43(1): 30-35.

Yu Hongbo, Feng Dazheng, Xie Hu. Iterative dimension-reduced robust adaptive beamformer for MIMO radar[J]. Journal of Xidian University, 2016, 43(1): 30-35. (in Chinese)