压缩感知中观测矩阵的优化算法
李 周 崔 琛
(国防科技大学电子对抗学院,安徽合肥 230037)
1 引言
压缩感知(Compressive Sensing,CS)理论[1]在采样率远小于奈奎斯特采样率的条件下获取信号的离散样本,然后通过非线性优化算法重构出原始信号。重构信号所需的采样率并不取决于信号的带宽,而与信号的稀疏度密切相关,因此CS有效降低了信号获取、存储及传输的代价[2],引起了越来越多学者的关注。
信号的稀疏表示、观测矩阵的构造、重构算法是CS理论中三个主要研究方向[3],其中观测矩阵是影响压缩感知性能的关键因素之一。观测矩阵构造的目的是如何采样得到观测值,并能从观测值中重构出原始信号。文献[4- 6]对精确重构所需观测矩阵的约束条件进行了研究:文献[4]提出了有限等距性质(Restricted Isometry Property, RIP),但判断观测矩阵是否符合RIP是组合复杂度的问题,实际用于观测矩阵的分析非常困难;文献[5- 6]提出了相关性的概念,其含义是观测矩阵与稀疏基之间的相关程度。研究表明,通过降低相关性可以减少CS的重构误差和精确重构原始信号所需的观测数。
文献[7]提出了一种对Gram矩阵中绝对值大于限定阈值的非对角元求平均的方法来表示观测矩阵与稀疏基的相关性,之后线性收缩 Gram矩阵中绝对值大于限定阈值的非对角元来降低相关性,取得了较好的实验效果。但是,该算法对Gram 矩阵进行奇异值分解来降阶计算下一轮迭代时的Gram矩阵时会产生绝对值较大的相关系数。为提高算法平稳收敛性,文献[8]用Welch 界作为观测矩阵和稀疏基相关系数的极限最小值,将非对角元均小于等于Welch界的Gram矩阵作为优化目标,使用梯度下降法逼近最优观测矩阵。但是算法中的步长因子b的选择对算法性能影响较大,需要由经验确定。
为提高CS的重构精度,本文对观测矩阵与稀疏基的相关性进行研究,提出了一种Gram矩阵的构造算法:首先将Gram矩阵与逼近等角紧框架 (Equiangular Tight Frame, ETF)的矩阵差的F范数作为目标函数,之后对目标函数进行最优化求解在理论上得到最优的Gram矩阵的解析式,最后本文在所推导出的最优Gram矩阵解析式的基础上使用迭代来优化观测矩阵。
2 观测矩阵基本架构
假定离散信号r∈Rl×1,若r中最多含有K个非零值且K≪l,那么r就称作K-稀疏的。将K-稀疏的信号集合记为:

(1)


(2)
如果变换后的s符合‖s‖0≤K≪l,即r可以用已知的稀疏基中少量的元素线性表示,那么r也被称作K-稀疏的。
CS理论的测量过程可以表示为[1]:

(3)


对于任意两个不同的稀疏信号r1,r2∈ΛK,必须满足Xr1≠Xr2,否则仅仅根据观测值无法区分r1,r2,因此感知矩阵需要满足一定的条件:对于任意K-稀疏的信号,只要其稀疏度K满足下式,信号即可准确地恢复出来[12]。
(4)
其中μ(X)指X任意两列xi和xj之间的内积绝对值的最大值[7],公式如下:
(5)
然而μ(X)仅表示观测矩阵与稀疏基之间列向量最大的相关性,是一种局部的相关性,因为在X只有某两列的相关性比较大,其余各列之间相关性比较小的情况下,就会出现相关系数μ(X)很大,感知矩阵X的性能并不差的情况。
因此文献[7]提出了表示总体相关性的t-平均相关性μt-aν,定义为X所有列向量两两之间的内积绝对值中大于限定阈值t的部分的平均值,或者是X所有列向量两两之间的内积绝对值中最大的t%部分的均值,其定义式如下:
(6)
其中gij为Gram矩阵G=XTX中的元素,gij为矩阵X的第i列xi与第j列xj的内积,Naν为Hav中的元素数目,即Gram矩阵非对角元|gij|大于t的数目或者所有|gij|中最大的t%部分的元素数目。仅阐述μt-aν为X任意两列内积绝对值大于t的平均值时Hav的定义:
Hav{(i,j):gij>t&i≠j}
(7)
为降低X任意两列的相关性,即减少Gram矩阵非对角元素的值,文献[7]采用如下阈值函数对Gram矩阵G中绝对值大于限定阈值的非对角元进行线性收缩,下式中t为阈值,γ为收缩因子。
(8)
当X中的列向量两两不相关时,其对应的Gram矩阵经列归一化后变成单位阵Il,基于此Elad提出了如下优化目标函数[7],使得Gram矩阵尽可能的接近单位阵Il,即使得观测矩阵与稀疏基的相关性尽可能为0。
(9)

(10)
仅当l≤m(m+1)/ 2时上式成立。
针对于压缩感知中Gram矩阵不可能为单位阵,Abolghasemi提出了如下优化函数[8]:
(11)


(12)
Abolghasemi将Gram矩阵进行如下收缩得到ETF矩阵Gt:
(13)

3 Gram矩阵的构造及观测矩阵的优化
本节将Gram矩阵与逼近ETF的矩阵Gt差的F范数作为目标函数,通过使目标函数对感知矩阵X的偏导等于零得到逼近Gt的一系列Gram矩阵,之后在一系列Gram矩阵中通过最小化目标函数在理论上选出最逼近Gt的Gram矩阵,最后将得到的Gram矩阵经阈值函数处理后作为下一轮迭代的Gt,使用迭代优化来降低Gram矩阵中非对角元的大小。
3.1 目标函数


(14)

3.2 Gram矩阵的构造
将感知矩阵X进行奇异值分解:
X=U(Σx0)VT
(15)



(16)


(17)

(18)
(19)
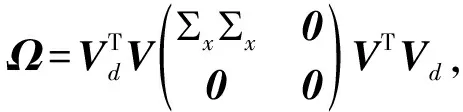



(20)

(21)
(22)
由式(22)可知G由V11和Σx唯一确定。

(23)

XGt=XXTX
(24)
将式(21)带入上式可得:
(25)

(26)

(27)

(28)
分别讨论上式中的三项:
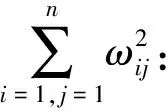


由式(25)可得:
(29)
(30)
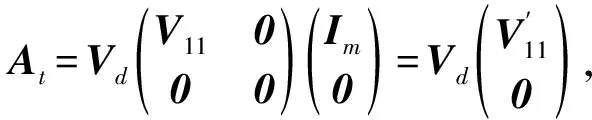


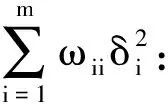
由于式(28)中前两项均为定值,所以:
(31)
由于:
(32)
(33)
因为
(34)

因为G=XTX为对称阵,Gt为G经阈值函数处理后的矩阵,所以Gt为对称阵,其奇异值分解可记为:
(35)

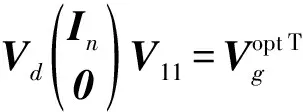
(36)

(37)

(38)
3.3 观测矩阵的优化算法
首先使用下式所示的阈值函数将Gram矩阵变为逼近ETF的矩阵。
(39)
其中ε为限定阈值,ε>μE,sign()为符号函数。
之后将式(37)求出的最优Gram矩阵经上述阈值函数处理后作为下一轮迭代的ETF,迭代优化减少感知矩阵的列相关性。迭代算法的具体步骤如下:

输出:观测矩阵Φ。
初始化:迭代次数k=1。
步骤:

2)对Gk进行列归一化;
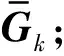

end

4 实验与分析

仿真中相关参数如下:m=30,n=l=100,信号的稀疏度K=10,CSElad方法中Gram矩阵收缩变换时非对角线的限定阈值(下文简称“阈值”)t=0.4,缩减倍数γ=0.2;CSAbolghasemi的K_iter=10,步长采用文献[8]中所用的b=0.05;CSOpt-to-Gt的阈值ε=0.4。为减少随机性对实验结果造成的影响,每次仿真均为1000次的蒙特卡罗仿真。
4.1 相关性
仿真实验1:
CSOpt-to-Gt,CSElad和CSAbolghasemi都是迭代进行的算法,将三种算法每次迭代时Gram矩阵的t-平均相关性μt-aν进行对比可以看出在各个算法迭代时t-平均相关性的变化趋势,进而对比出三种算法在t-平均相关性这一方面的优劣性。t-平均相关性μt-aν中的参数t=20%,其含义是Gram矩阵非对角元中最大的20%部分的均值。
由图1可知,随着迭代的进行三种优化算法优化的观测矩阵与稀疏基的相关性逐渐减少,CSOpt-to-Gt的相关性最小,CSAbolghasemi的相关性次之,CSElad的相关性最大,且CSElad由于降阶计算观测矩阵时会产生比较大的非对角元故随迭代进行其μt-aν变化范围较大。原因分析如下:

图1 三种算法得到的Gram矩阵所对应的μt-aν随着迭代次数的变化
(1)阈值函数不同:CSElad线性收缩Gram矩阵中较大的非对角元,而CSAbolghasemi与CSOpt-to-Gt直接使用较小的阈值限定Gram矩阵中非对角元最大值,故CSElad的Gram矩阵中非对角元的最大值大于CSAbolghasemi与CSOpt-to-Gt。
(2)优化方法不同:CSOpt-to-Gt使用理论上最优的Gram矩阵直接求出最逼近Gt的Gram矩阵,其中Gt为Gram矩阵经过阈值函数处理后逼近ETF的矩阵,而CSElad在每次迭代中线性收缩Gram矩阵的非对角元,CSAbolghasemi在每次迭代中在梯度方向上求解Gram矩阵,CSElad和CSAbolghasemi只是利用了不同的方法使Gram矩阵逼近各自的Gt,并不是求解最优的Gram矩阵,故CSOpt-to-Gt所求出的Gram矩阵更加接近Gt。
4.2 算法的重构性能

(40)
仿真实验2:
稀疏度K对算法的重构性能有直接的影响:在给定观测次数的前提下,稀疏度越高,重构误差越大。为了得出稀疏度K对各个算法重构性能的影响,仿真稀疏度K由8变化到16时三种算法的MSE的变化情况,如图2所示。

图2 稀疏度变化时三种算法的MSE变化情况
图2中6≤K≤10时三种算法的重构误差曲线重合在一起,下表列出了6≤K≤10时三种算法的重构误差数值。

表1 K变化时三种算法的MSE对比表
由图2与表1可知三种算法的MSE随着稀疏度K的增加而逐渐加大,在稀疏度K<12时CSOpt-to-Gt的重构误差比CSElad和CSAbolghasemi小但优势不明显,当K≥12时CSOpt-to-Gt的重构误差远小于CSElad和CSAbolghasemi。
仿真实验3:
观测次数M对压缩感知的重构误差有直接的影响:M越大,重构误差越小;M越小,重构次数越小。仿真了稀疏度K=10,观测次数M从20增加到34时三种算法重构误差的变化情况,如图3所示。

图3 观测次数变化时三种算法的MSE变化情况
图3中30≤M≤34时三种算法的重构误差曲线重合在一起,为便于查看,下表列出了30≤M≤34时三种算法的重构误差数值。

表2 M变化时三种算法的重构误差对比表
由图3与表2可以看出CSOpt-to-Gt在观测次数M≤24时重构误差远小于CSElad和CSAbolghasemi,在M≥26时CSOpt-to-Gt重构误差略小于CSElad和CSAbolghasemi。
由仿真实验2与3可得CSOpt-to-Gt的MSE在稀疏度高或者观测次数少的情况下远小于CSElad和CSAbolghasemi。这是由于CSOpt-to-Gt产生的观测矩阵与稀疏基的相关性小于CSElad和CSAbolghasemi,可以更好地保持不同K稀疏向量之间的距离。在观测次数多或者稀疏度K低时观测矩阵与稀疏基的相关性较大也可保持不同K稀疏向量之间一定的距离,故三者的MSE差别不大;在观测次数少或者稀疏度K高时相关性必须小才可以保持不同K稀疏向量之间一定的距离,此时CSElad和CSAbolghasemi由于相关性大不能保持任意不同的K稀疏向量之间一定的距离,故CSOpt-to-Gt的MSE远小于CSElad和CSAbolghasemi。
4.3 运行时间
仿真实验4:
为了研究本文所提算法的复杂度,该仿真实验统计CSOpt-to-Gt、CSElad和CSAbolghasemi三种算法优化后的观测矩阵与稀疏基的t-平均相关性μt-aν达到0.28所需要的运行时间。虽然算法的运行时间不能严格地定义算法复杂度,却可以在一定程度上对算法的复杂度做出描述。这里,我们的仿真环境为2.53 GHz英特i5四核处理器、4 GB内存Win10 系统下的 MATLAB R2014a。图4给出了信号长度N变化时各算法对应的运行时间。

图4 算法运行时间的比较
由图4可以看出,当信号的长度增加时,三种算法的运行时间也会增长,其中:CSOpt-to-Gt算法的运行时间增长最快,CSAbolghasemi次之,CSElad的运行时间增长最慢。原因分析如下:CSOpt-to-Gt在3.3小节所示的算法中的第(4)步与第(7)步均需要计算运算量较大的矩阵奇异值分解;CSAbolghasemi利用内层迭代在梯度方向上对观测矩阵进行迭代优化,在每一轮的迭代中均需要求解梯度运算;CSElad则是将Gram矩阵经过阈值函数收缩后利用计算量小但精度较低的矩阵求逆计算出观测矩阵。
但总体上看,相对于在相关性与重构精度方面的优势而言,CSOpt-to-Gt增加的运行时间是可接受的。
5 结论
为提高稀疏信号的重构精度和观测矩阵优化时的收敛平稳性,本文对观测矩阵与稀疏基的相关性进行研究,提出了一种稀疏基已知的前提下面向观测矩阵优化的Gram矩阵构造算法。该算法首先将Gram矩阵与逼近ETF的矩阵差的F范数作为目标函数,后对目标函数进行最优化求解在理论上得到最优Gram矩阵的表达式,最后将产生的Gram矩阵经阈值函数处理后作为下一轮迭代时目标函数中逼近ETF的矩阵,使用迭代优化降低感知矩阵的列相关性。仿真表明,在相同的实验条件下,该算法在观测矩阵与稀疏基的相关性方面优于现有算法,在观测次数少或者稀疏度高的情况下具有更高的重构精度。如何优化阈值函数来构造性能更优的观测矩阵以及如何由最优的Gram矩阵得到相应的观测矩阵是下一步的研究方向。
[1] Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2004, 52(2):489-509.
[2] 马坚伟,徐杰,鲍跃全,等, 压缩感知及其应用:从稀疏约束到低秩约束优化[J]. 信号处理, 2012, 28(5): 609- 623.
Ma Jianwei, Xu Jie, Bao Yuequan, et al. Compressive Sensing and its Application: from Sparse to Low-rank Regularized Optimization[J]. Signal Processing, 2012, 28(5): 609- 623.(in Chinese)
[3] 王军华,黄知涛,周一宇,等. 压缩感知理论中的广义不相关性准则[J]. 信号处理, 2012, 28(5): 675- 679.
Wang Junhua, Huang Zhitao, Zhou Yiyu, et al. Generalized Incoherence Principle in Compressed Sensing[J]. Signal Processing, 2012, 28(5): 675- 679.(in Chinese)
[4] Donoho D L, Elad M. Optimally Sparse Representation in General (Nonorthogonal) Dictionaries via l1Minimization[J]. Proceedings of the National Academy of Sciences of the United States of America, 2003, 100(5):2197.
[5] Gribonval R, Nielsen M. Sparse representations in unions of bases[J]. Information Theory IEEE Transactions on, 2011, 49(12):3320-3325.
[6] Tropp J A, Dhillon I S, Heath R W, et al. Designing structured tight frames via an alternating projection method[J]. IEEE Transactions on Information Theory, 2005, 51(1):188-209.
[7] Elad M. Optimized Projections for Compressed Sensing[J]. IEEE Transactions on Signal Processing, 2007, 55(12):5695-5702.
[8] Abolghasemi V, Ferdowsi S, Sanei S. A gradient-based alternating minimization approach for optimization of the measurement matrix in compressive sensing[J]. Signal Processing, 2012, 92(4):999-1009.
[9] 麻曰亮,裴立业,江桦. 改进的压缩感知测量矩阵优化方法[J]. 信号处理, 2017, 33(2): 192-197.
Ma Yueliang, Pei Liye, Jiang Hua. Improved Optimization Algorithm for Measurement Matrix in Compressed Sensing[J]. Journal of Signal Processing, 2017, 33(2): 192-197.(in Chinese)
[10]肖小潮, 郑宝玉, 王臣昊. 基于最优观测矩阵的压缩信道感知[J]. 信号处理, 2012, 28(1):67-72.
Xiao Xiaochao, Zheng Baoyu, Wang Chenhao. Compressed Channel Estimation based on Optimized Measurement Matrix[J]. Signal Processing, 2012, 28(1): 67-72. (in Chinese)
[11]Kwon S, Wang J, Shim B. Multipath Matching Pursuit[J]. IEEE Transactions on Information Theory, 2014, 60(5):2986-3001.

