场道钢筋加固区的灾害目标检测

曹芸茜 吴仁彪 何炜琨

(1. 中国民航大学智能信号与图像处理天津市重点实验室，天津 300300; 2. 中国民航大学基础实验中心，天津 300300)

1 引言

机场作为城市和航空运输的基础设施，是交通运输的重要组成部分。机场道面是机场建设的核心，跑道质量的好坏将会直接影响机场与飞机运行的安全，其中场道内脱空和裂缝等隐性灾害的检测和维护至关重要[1]。在不影响机场正常运行且不破坏道面结构的基础上，对道面进行无损检测是必然趋势。探地雷达(Ground Penetrating Radar, GPR)是一种有效的无损检测工具，其具有探测速度快、操作方便、分辨率高等特点[2-3]。在机场场道的建设施工中，为了加强其承载能力，需要铺设钢筋进行加固[4]。钢筋的强反射回波甚至多次反射后的回波都会淹没灾害目标的回波，所以有效的抑制钢筋强反射回波对灾害目标的检测是十分关键和必要的。

本文首先利用非一致性检测对探地雷达接收数据进行预处理，利用时变增益函数对钢筋反射一次回波进行粗抑制，然后对该数据在时间维进行分段均衡，以滤除钢筋在机场场道下各层分界面的多次反射回波，再利用时频—时空域二重S变换方法对灾害目标进行检测，并同时显示其在场道下的空间位置。该方法能在灾害目标回波信号被钢筋多次强反射回波信号淹没的情况下，有效抑制钢筋对灾害目标的影响，达到检测道面下微小灾害目标空间位置的目的，为机场养护施工提供直观依据。

2 信号模型

探地雷达接收信号模型可以表示为：

w(t)=o(t)+d(t)+s(t)

(1)

如图1所示，o(t)表示收发天线直接耦合波，在收发天线间距确定后直接耦合波分量一般相对固定。d(t)表示各层媒质表面反射回波，由于探测环境往往是变化的，所以d(t)的变化性和不可预测性较大。s(t)表示媒质内目标反射回波，也就是我们需要的回波分量。

图1 GPR信号模型

我们将目标反射回波s(t)进行采样，那么二维B-Scan数据中，雷达测试线l=1,2,…,L的第i=1,2,…,T个采样点的目标反射回波信号可以表示为sl(i)。

3 钢筋回波抑制

本节研究钢筋的强反射回波及多次反射后回波的抑制方法。首先利用基于广义内积的非一致性检测对探地雷达接收数据进行预处理，然后利用时变增益函数对钢筋的一次强反射回波进行粗抑制，最后利用时间域的分段均衡算法抑制钢筋的多次反射回波。

3.1 预处理

我们将探地雷达接收到的回波信号w(t)进行预处理，去除直接耦合波o(t)和各层媒质表面反射回波d(t)，以提取出钢筋及灾害目标的反射回波s(t)。

首先去除探地雷达接收到的回波信号中收发天线间的直接耦合波o(t)。我们可以将雷达天线对准开阔无物体的空间，或将天线置于暗室内，录取对空信号，此信号可以近似为直接耦合信号，再将雷达接收回波减去此直接耦合信号即有效去除了直接耦合波。

然后去除机场场道下各层媒质表面反射回波d(t)。由于探测环境的变化，d(t)的变化性和不可预知性较大，所以，我们需要根据探测区域的数据对d(t)进行有效的去除。这里，我们采用基于广义内积的非一致性检测方法合理去除d(t)。

基于广义内积的非一致性检测算法，其输出定义为：

(2)

其中l=1,2,…,L为雷达测试线数，xl为去除直接耦合波后的雷达采样数据的矩阵表示，Rl为自相关矩阵，其可以表示为：

(3)

计算出雷达所有探测点的gl(GIP)后，给出阈值，大于此阈值则说明与周围差异较大，则可认为此部分探测区域存在目标反射信号，我们将此类区域数据滤除，剩下的小于阈值部分的回波即为各层媒质表面强反射回波，选取该回波信号作为背景回波，将雷达接收回波减去背景回波即可以有效去除各层媒质表面反射回波而有效的保留了目标反射回波。

3.2 钢筋回波抑制

在机场跑道使用过程中，初期常见的隐性灾害主要有脱空和裂缝[5- 6]。脱空主要出现在面层和上基层的交界处，裂缝主要出现在面层，而加固的钢筋主要位于面层的上部，如图2所示，所以钢筋的强反射回波会严重影响甚至淹没脱空和裂缝的反射回波，并且钢筋与场道各层介面的多次反射回波也会严重影响场道灾害目标的检测，所以有效地抑制钢筋的强反射回波对灾害目标进行检测是十分关键和必要的。

图2 钢筋及灾害目标分布模型

由于钢筋的一次反射回波远远强于多次反射回波，且多次反射回波往往会与灾害目标反射回波混叠，不易处理，所以我们将钢筋回波抑制分为两步，第一步利用时变增益函数对钢筋一次反射回波进行粗抑制，第二步利用时域分段均衡方法对钢筋的多次反射回波进行细抑制，以便提取出有效的灾害目标反射回波。

3.2.1粗抑制—时变增益

机场场道在进行钢筋加固时有严格的规范并且有先验的钢筋位置信息，我们可以根据钢筋位置的先验知识，构造合适的时变增益函数Pl(t)，其中l=1,2,…,L为雷达测试线，将其采样后记为Pl(i)，那么时变增益后的雷达数据为

ul(i)=Pl(i)·sl(i),i=1,2,…,T,l=1,2,…,L

(4)

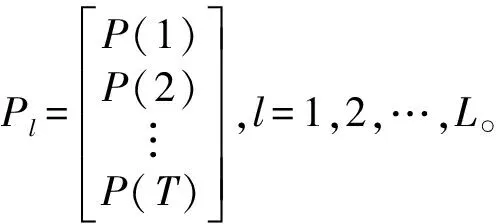
时变增益函数可以抑制钢筋一次强反射回波时间窗内数据，增强需要观察的机场场道面层及基层时间窗内数据，抑制不需要观察的场道底部数据，即选择需要观察的数据予以增强，不需要观察的数据予以抑制，对钢筋的一次反射回波进行粗抑制，此方法可以有效抑制钢筋一次反射回波，而增强了灾害目标反射回波，但是钢筋的多次反射回波也同灾害目标反射回波一同被增强，所以我们还要对钢筋的多次反射回波进一步抑制。

3.2.2细抑制—分段均衡

如果某一深度存在目标，则此深度目标所在位置必与同一深度其他位置的回波有差异且钢筋对各层表面多次反射回波呈现较强的规律性，所以本文提出分段均衡的方法，对B-Scan数据进行时间维分段，再利用数据信息求出分段矢量，对每一段数据进行均衡，这样可以对相对规律的数据进行均衡滤波，对存在局部差异的数据起到增强的效果，有利于细节的辨认。本文利用分段均衡的方法来抑制钢筋的多次反射回波。

首先计算钢筋粗抑制后的数据中所有雷达测试线l=1,2,…,L在第i个采样点的平均值：

(5)

根据灾害目标的厚度合理选取分段数据点数m=T/K，其中K为分段数目，T为总时间采样点数。局部搜索第k=1,2,…,K段的最大值maxk及最小值mink，定义差值矢量为

d=[max1-min1max2-min2…maxK-minK]

(6)

为了方便将上式记为

d=[d1d2…dk]

(7)

设dmax为d中最大值，定义均衡放大矢量为

a=[d1/dmaxd2/dmax…dK/dmax]

(8)

记为a=[a1a2…ak]。

钢筋粗抑制后的B-Scan接收数据用矩阵可以表示为u。根据上述分段方法，按照相同原理对u在时间维进行同样的分段。设uk为对u进行分段的第k段数据，则uk可以表示为：

uk={ul(i),i=(k-1)m+1,(k-1)m+2,…,km;

l=1,2,…,L;k=1,2,…,K}

(9)

利用每一段数据的均衡放大系数对相应的该段数据进行加权均衡，得到第k段数据的均衡处理结果：

yk=akuk

(10)

其中，k=1,2,…,K。那么，B-Scan接收数据的均衡处理结果可以表示为：

Y=[y1y2…yK]T

(11)

4 灾害目标检测

钢筋回波抑制后的数据在灾害目标附近可能还会存在少许干扰回波，这也会干扰体积或厚度较小的灾害目标，譬如小裂缝、脱空薄层的检测。本文提出了时频—时空域二重S变换灾害目标检测方法，可以有效的检测体积及厚度较小的灾害目标。

S变换[7-9]是基于短时窗傅里叶变换和小波变换提出来的一种时频分析方法，该方法吸收了两者的优点，同时克服了它们的缺点。

设函数h(t)∈L2(R)(L2(R)表示能量有限的函数空间)的S变换的定义如下：

(12)

S变换的基本小波定义为：

(13)

(14)

由式(14)可以看出，S变换采用宽度随频率呈反比变化的高斯窗函数，低频段的时窗较宽，可以获得较高的频率分辨率，高频段的时窗较窄，可获得较高的时间分辨率[10]。利用高频段时间分辨率较高的特性可以有效的检测出体积及厚度较小的灾害目标。

首先选取均衡后数据Y中的A-Scan数据yl(t)，雷达测试线l∈[1,L]。对yl(t)进行时间—频率维S变换：

(15)

根据S变换结果选取时间分辨率较高的频率段f0…fN，固定该频率段中的一个频率点fn(n∈[0,N])，在该频率点下对yl(t)再次进行S变换：

(16)

对B-Scan数据Y中的所有测试线l=1,2,…,L的数据yl(t)分别进行S变换，即可得到一个固定频点fn的时间—距离维S变换结果：

Sfn(τ,l)={Sl(τ,fn),l=1,…,L}

(17)

将选取的频率段f0…fN中所有频点的时间—距离维S变换数据叠加，进行频域均衡滤波：

(18)

根据叠加结果不但可以有效检测出体积及厚度较小的灾害目标，还可以得到灾害目标的空间位置。

综上所述，机场场道钢筋加固区的灾害目标检测方法的流程如图3所示。

图3 灾害目标检测方法流程

5 仿真结果与分析

为了验证本文方法的有效性，实验中所有数据均由GPRMAX2.0[11]高保真仿真软件产生，采用双基地探地雷达，选取天线间距为0.1 m，距地面高度为0.04 m，发射信号采用ricker波脉冲形式，中心频率为900 MHz，采集数据时间窗为25 ns，采集测试线间距为0.02 m，共采集118道数据。仿真模型为一般机场场道基本四层模型，层厚从上到下依次为0.34 m,0.20 m,0.20 m,0.26 m，介电常数依次为9,12,15,22。

图4为本实验中所采用的机场道面仿真数据原始几何模型图，该模型中含有五根钢筋，一条裂缝和一个脱空，钢筋均匀分布在面层中距地表面17 cm，每条钢筋间距为50 cm，裂缝长18 cm，宽5 mm，脱空宽20 cm，厚7 mm。

图4 原始数据几何模型

图5为探地雷达接收到的二维B-Scan回波数据。由于地表反射回波很强，淹没了地下目标的回波信息，所以首先必须有效的去除地表反射回波，提取需要的回波信息。图6为利用非一致性检测滤除背景回波后的目标反射回波。背景的四层媒质表面反射回波被有效滤除，凸显出地下目标的反射回波，但是由于场道浅层钢筋反射回波很强，且存在钢筋多次反射回波，严重影响甚至淹没钢筋下灾害目标的回波，无法有效地检测出灾害目标，尤其是细小的裂缝。

图6 目标反射回波数据

根据图6所示数据，选择合适的时变增益时窗，对强金属回波及不需要观察的场道深层处数据进行抑制，对需要观察的数据段进行增强，如图7所示。图8为钢筋回波粗抑制后B-Scan数据，脱空的反射回波被增强，可以观察到，但是由于裂缝上下表面比较窄，反射回波很弱，并且钢筋与地下各层媒质表面的多次反射回波也比较强，所以裂缝还是不能有效观测。图9为分段均衡后B-Scan数据，钢筋在各层媒质间的多次反射回波被有效均衡，突出了脱空的反射回波，但仍无法有效检测出灾害目标。

图7 时变增益

图8 钢筋回波粗抑制

图9 钢筋回波细抑制

图10为均衡滤波后采集数据进行时间—频率维S变换的时频分析结果，我们选取其中时间分辨率较高的高频段2500～2900 MHz数据，先确定该频段内的一个频点，对均衡后B-Scan数据进行时间—距离维S变换，将所有频段内的S变换结果进行频域均衡滤波，得到如图11所示结果，可以明显检测出脱空及裂缝的存在。图12为不进行均衡滤波而直接用相同的方法进行S变换的结果，虽然能够检测到脱空，但是不能有效地检测到裂缝的存在，且钢筋的多次反射回波严重影响了灾害目标的检测。

图10 S变换时频分析

图11 灾害目标检测结果

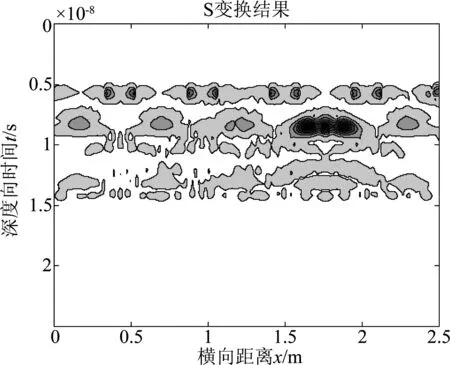
图12 未分段均衡检测结果

6 结论

考虑到钢筋的强反射回波对场道钢筋加固区灾害目标检测的影响，本文首先提出时变增益函数和分段均衡的方法对钢筋的多次反射回波进行抑制，然后提出时频—时空域二重S变换方法对灾害目标进行检测。仿真结果表明本文算法可以有效去除钢筋的多次反射回波对厚度及体积较小的常见灾害目标回波的影响，对灾害目标进行检测并显示其在场道下的空间位置，为机场场道的养护施工提供直观的依据。

[1] 翁兴中,蔡良才.机场道面设计[M].北京:人民交通出版社,2007.

Weng Xingzhong, Cai Liangcai. Design of Airport Runway[M].Beijing: China Communications Press, 2007.(in Chinese)

[2] 何炜琨, 吴仁彪, 刘家学. 基于探地雷达的机场场道脱空层检测及厚度估计[J]. 信号处理, 2011, 27(10):1547-1551.

He Weikun, Wu Renbiao, Liu Jiaxue. Void-layer Detection and Depth Determination in Runways based on GPR[J]. Signal Processing, 2011, 27(10):1547-1551.(in Chinese)

[3] Hoarau Q, Ginolhac G, Atto A M, et al. Robust Adaptive Detection of Buried Pipes using GPR[C]∥24th European Signal Processing Conference, 2016:533-537.

[4] Harry M J. Ground penetrating radar theory and applications[M]. London: Elsevier, 2009.

[5] 何炜琨. 基于探地雷达的机场场道质量监测关键技术研究[D]. 天津：天津大学, 2012.

He Weikun. Enabling Techniques for Runways Quality Surveillance via Ground Penetrating Radar[D]. Tianjin: The University of Tianjin, 2012.(in Chinese)

[6] 庞希斌, 徐进, 卢小宾, 等. 地质雷达在机场跑道缺陷检测中的应用——以“5·12”汶川地震后九寨黄龙机场检测为例[J]. 西南民族大学学报, 2008, 34(6):1096-1100.

Pang Xibin, Xu Jin, Lu Xiaobin, et al. Application of the ground penetrating radar to the inspection of the airfield runway defect——Taking the detection of Jiuhuang Airport after the 5.12 Wenchuan earthquake for example[J]. Journal of Southwest University for Nationalities Natural Science Edition, 2008, 34(6):1096-1100.(in Chinese)

[7] Yan Jin, Liu Jie. Parameter estimation of frequency hopping signals based on the Robust S-transform algorithms in alpha stable noise environment[J]. International Journal of Electronics & Communications, 2016, 70(5): 611- 616.

[8] Kazemi K, Amirian M, Dehghani M J. The S-transform using a new window to improve frequency and time resolutions[J]. Signal, Image and Video Processing, 2014, 8(3): 533-541.

[9] 刘志成, 王殿伟. 非线性调频信号的自适应时频滤波算法[J]. 信号处理, 2015, 31(3):356-363.

Liu Zhicheng, Wang Dianwei.Adaptive Time-Frequency Filter Method of Nonlinear Frequency Modulation Signal[J]. Journal of Signal Processing, 2015, 31(3):356-363.(in Chinese)

[10]Huang Nantian, Peng Hua, Cai Guowei, et al. Power Quality Disturbances Feature Selection and Recognition Using Optimal Multi-Resolution Fast S-Transform and CART Algorithm[J]. Energies, 2016, 9(11): 1-21.

[11]GprMax2.0[OL]. http:∥www. gprmax.org.