浅析“类比思想”在初中数学教学中的应用
陈美荣

[摘 要] 应用“类比思想”,巧读数学教材,能凸显类比思想的重要性;应用“类比思想”,巧学数学知识,体现在引入数学新概念及启发学生探究思考上;应用“类比思想”,巧解中考试题,表现在通过条件类比寻找解题突破,利用性质类比凸显思维活动上.
[关键词] 类比思想;初中数学;中考
类比思想简单来讲就是分类对比,根据两个对象的一些相似属性,猜想它们的另外一些属性也可能相同或相似. 这种思维方法对学生掌握数学学习方法,培养数学思维能力,至关重要. 一位伟人曾经指出:“类比是一个伟大的引路人. ”类比能让学生经历探究学习过程,能培养学生的直觉思维、合情推理能力和归纳演绎能力.
应用“类比思想”,巧读数学教材
类比思想是初中数学的重要思想之一,是学生必须掌握与理解的重要思维,在初中数学教科书中有诸多体现.
在代数的学习过程中,教材内容便体现了类比思想. 譬如,一元一次不等式是初中数学的难点和重点,因此,在阐述该知识点时,教材非常注意将其与一元一次方程进行类比,发现其定理、性质与运算过程基本类似,所以将二者进行类比分析,学习起来事半功倍.
同样,类比思想也蕴藏在数学教材的几何知识方面. 例如,教材将度、分、秒的运算原理和注意事项与时、分、秒的运算原理和注意事项进行类比分析,发现二者异曲同工. 再如,三角形相似是几何知识的难点之一,很多学生对其一知半解,所以教材讲解该部分时非常注意方法的传授. 其实,相似三角形与全等三角形的性质、定理与推理过程存在很多相似之处,故讲授时一定要注意类比分析,促进学生对该知识点的理解与把握,进而增强教学的有效性.
应用“类比思想”,巧学数学知识
类比教学方法在日常数学教学过程中,应用非常广泛,主要体现在概念教学、数学定理与运算法则及探究教学方面,基本涉及数学教学的方方面面.
1. 巧用类比思想,引入数学新概念
概念是事物内涵与外延的最基本定义,是研究事物的基础与关键,数学概念在数学学习中也不例外. 类比思想在沟通新旧知识方面起着桥梁的作用. 如果将数学概念与类比思想结合起来考量与应用,则能够有效降低学生对数学概念的陌生感,进而摒弃排斥心理,乐于花时间和精力来学习数学知识. 例如,教师在教授“分式”概念及基本性质时,可以将“分数”和“分式”进行类比,寻找二者的相似与不同之处,以下是教学片段.
师:小学里我们学过分数,那什么叫分数?分数有哪些性质?
生:两个整数相除的式子叫分数,分数的分母不能为零. 分数的分子和分母同时乘(或除以)一个不为零的数,分数的值不变.
师:出现用字母代表数之后,我们把分母里含有字母的式子叫分式. 你认为分式中的字母有没有制约条件?为什么?
……
分式与学生已学的分数联系密切,教师通过问题引导、复习,能激活学生的原有认知结构,为新知识的类比学习做铺垫. 同时,也顺理成章地让学生理解分式有无意义的条件、值为零的情况及分式的基本性质,为新知识的学习铺平道路.
由此可见,在概念教学中应用类比思想,能使新概念的得出更加自然,同时,由于在学生的“最近发展区”,所以降低了学生初次接触新概念的陌生感. 把对新概念下定义的主动权交给学生时,教师只要适时引导,就能激发学生学习数学的积极性,体现“学为中心”的理念.
2. 巧用類比思想,启发学生探究思考
类比思想的应用不仅体现在概念方面,而且体现在数学定理与运算法则方面. 数学定理与运算法则的推理过程蕴含着类比思想,对学生数学思维能力的培养至关重要. 例如,教学“相似三角形的判定”时,可以在复习“全等三角形的判定定理”基础上进行类比教学.
全等三角形的判定定理有:(1)边角边定理,即SAS;(2)角边角定理,即ASA;(3)角角边定理,即AAS;(4)边边边定理,即SSS;(5)直角三角形中的斜边直角边定理,即HL. 那么对于相似三角形的判定,是否也有类似的定理呢?
……
利用类比的方法进行教学,既可以复习已学的全等三角形知识,又可以进一步认识新学的相似三角形;既能找到它们的相似之处,又能找到它们的不同之处,有助于学生对数学知识的理解与吸收.
2011年国家颁布最新《全日制义务教育数学课程标准》,明确提出“四基”目标与培养学生合情推理与演绎推理等能力的要求,希望进一步提高数学思维能力在教学中的重要性,而类比思想在定理教学过程中,注重知识间的联系,即新、旧知识间的联系,有利于培养学生掌握与应用数学的能力与思维,有利于培养学生的自学与动手操作能力,能增强学生对定理与推理过程的理解,体现以学定教,同时培养学生的数学核心素养.
应用“类比思想”,巧解中考试题
中考是对学生初中三年数学学习的集中考核,在一定程度上能折射出学生的数学思维能力,能体现择优选拔的理念,故中考题往往注重对学生类比、迁移、推理等能力的考查. 仔细研究近几年的数学中考试题会发现,对类比思想的考查所占比重较大,且主要体现在条件类比型、性质类比型这两方面. 所以,在日常教学过程中我们一定要重视对学生类比思想的教学与培养,以适应中考考试动态的需要与社会的发展.
1. 通过条件类比,寻找解题突破
条件类比是两个对象(通常是定理、公式与对应法则等)之间的条件关系类比,是对学生逻辑思维能力的集体考查,以“一线三直角问题的再探究”为例,具体如下.
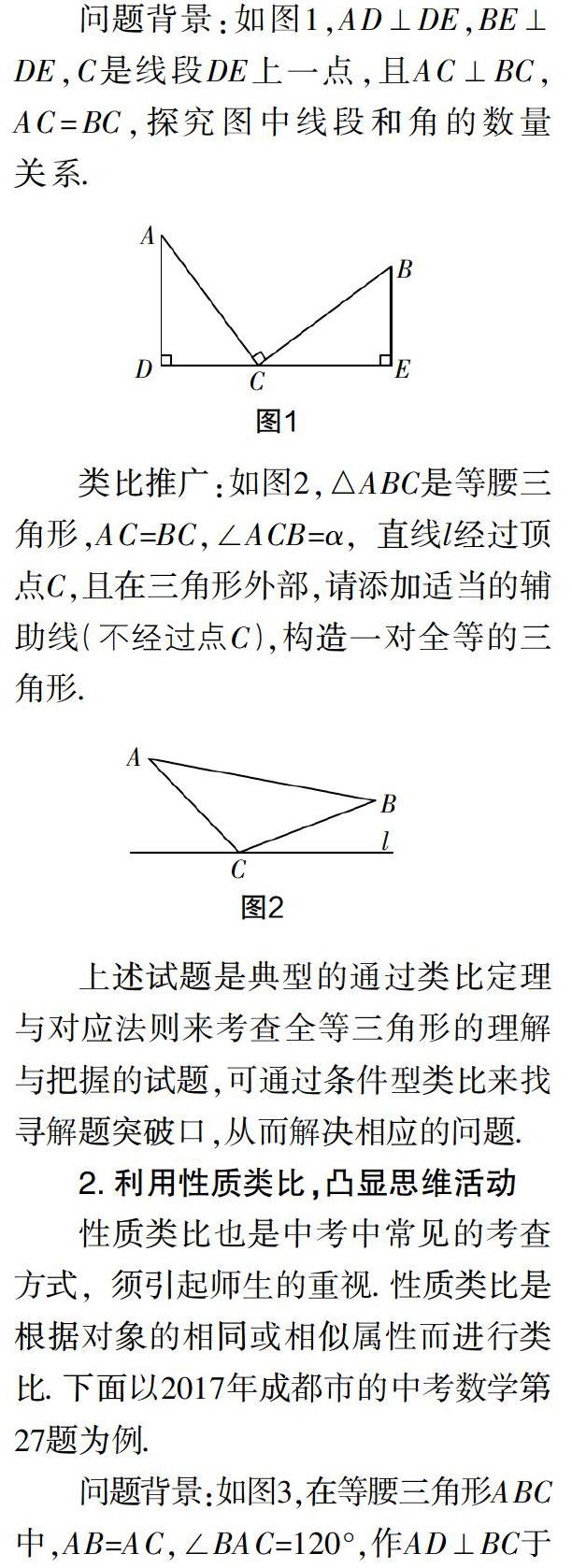
问题背景:如图1,AD⊥DE,BE⊥DE,C是线段DE上一点,且AC⊥BC,AC=BC,探究图中线段和角的数量关系.
类比推广:如图2,△ABC是等腰三角形,AC=BC,∠ACB=α,直线l经过顶点C,且在三角形外部,请添加适当的辅助线(不经过点C),构造一对全等的三角形.
上述试题是典型的通过类比定理与对应法则来考查全等三角形的理解与把握的试题,可通过条件型类比来找寻解题突破口,从而解决相应的问题.
2. 利用性质类比,凸显思维活动
性质类比也是中考中常见的考查方式,须引起师生的重视. 性质类比是根据对象的相同或相似属性而进行类比. 下面以2017年成都市的中考数学第27题为例.
问题背景:如图3,在等腰三角形ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点.
迁移应用:如图4,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)请直接写出线段AD,BD,CD之间的等量关系式.
拓展延伸:如图5,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(1)证明:△CEF是等边三角形.
(2)若AE=5,CE=2,求BF的长.
本题通过相关知识的迁移应用来考查学生的类比思想,是典型的性质类比. 关于性质类比类的试题,中考往往将其作为压轴题,考的次数不多,但分值都比较重,是一道有难度与区分度的试题,教师在日常教学中要特别注意.
拉普拉斯曾言:“甚至在数学里,发现真理的主要工具也是归纳与类比. ”拉普拉斯高度认可了类比在认知科学中对人类思维能力形成及认识与改造自然界和人类社会的重要性. 在初中数学教学中恰当地应用“类比思想”教学方法,能增强学生对概念、定理与推理过程的理解,能培养学生掌握与应用数学的能力与思维,能培养学生的自学与动手操作能力.

