具有丢包补偿的分布式一致性融合估计器

赵国荣，廖海涛，韩 旭，王元鑫

（海军航空大学，山东烟台264001）

近年来，网络化多传感器融合估计以其一系列优点已被广泛应用于环境监测、目标跟踪、导航定位等领域[1-7]。分布式一致性融合估计算法以其收敛速度快、融合精度高等优点引起了广泛的关注与研究[8-12]。该类算法中每个传感器节点均能视为融合节点，通过利用局部信息一致化全局信息，最终使得所有传感器节点对目标的估计趋于一致[13-16]。文献[13]设计了一种卡尔曼一致性滤波算法（KCF），各传感器节点接收邻居节点的测量值、状态估计值和协方差值并进行一致化处理，使得所有传感器节点的估计值趋于一致。为了提高KCF算法的估计精度和一致性，文献[14-15]分别对KCF算法进行了改进。前者通过对协方差矩阵进行加权一致化处理，提出了一种信息矩阵加权一致性滤波算法（IM-KCF），并对加权系数进行了优化。后者则是通过一致化邻居节点前一时刻的状态估计值来修正局部状态预测值，并给出了一种一致性增益的取值方法。文献[16]通过设计滤波器增益的方法提出了一种基于一致性的线性滤波算法，该算法仅需交换各节点的局部状态估计值，相比KCF算法计算量大大减少。以上文献均没有考虑网络丢包问题。

在实际的应用中，由于网络堵塞、外界干扰、传感器故障等因素影响，网络丢包不可避免。丢包问题往往造成分布式一致性估计算法的估计精度变差、抗干扰能力减弱，甚至导致系统变得不稳定。目前，针对这一问题已有一些研究。文献[17]提出了带丢包的分布式一致性滤波算法，并发现通过对起“领导”作用的传感器节点进行控制可以降低丢包对融合性能的影响。文献[18-19]通过设计自适应一致性权重值来解决数据丢包的问题，不同的是文献[18]是根据各节点的估计值偏差大小来自适应修正一致性参数值，而文献[19]则是利用模糊集合理论将不同节点对目标状态不同的估计确信度引入到一致性权重值的更新中。以上文献均着重考虑观测数据丢失下的融合算法设计，且对观测丢失没有补偿，对局部状态估计值的丢失问题没有进行研究。在分布式一致性框架下，各节点间局部状态估计值的交换对估计器的融合性能起着至关重要的作用。因此，局部估计值的丢失问题不容忽视。

基于以上分析，区别于文献[17-19]，本文考虑的随机丢包现象存在于各传感器节点间局部状态估计值传输的过程中，并对丢包进行了补偿。考虑到求得最优局部估计器增益的解析形式较为困难，利用不等式理论得到了一组次优估计器增益。同时，基于Lyapunov理论对算法的稳定性进行了分析。最后，通过数值仿真验证了算法的有效性。

1 问题描述

考虑如下线性离散动态随机系统：

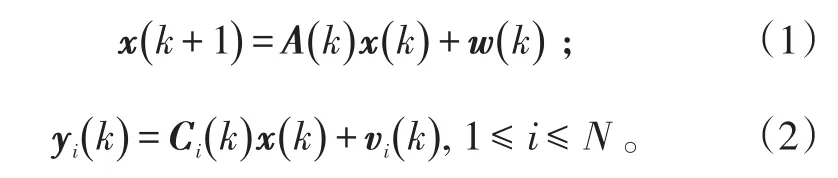
式（1）、（2）中：x(k)∈ℝn和分别表示系统的状态和第i个传感器的测量输出；A(k)∈ℝn×n和Ci(k)∈ℝmi×n表示系统矩阵和测量矩阵；系统噪声w(k)∈ℝn和测量噪声是零均值互不相关白噪声，且满足：

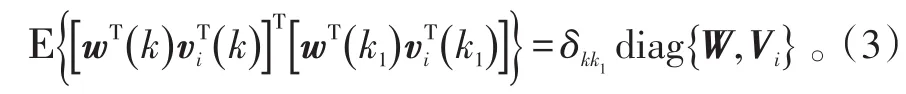
式（3）中：W和Vi分别是系统噪声和测量噪声的协方差矩阵；Ε{∙}表示数学期望。

假设系统初始状态值x(0)=x0，x0服从期望为μ0、协方差矩阵为P0的高斯分布，且与w(k)、vi(k)互不相关。

在分布式一致性融合框架下，各传感器节点均能视为融合节点。第i个传感器节点分两步计算得到分布式一致性融合状态估计值(k)。

Step 1：传感器节点j(j=1,2,…,N)采用Luenberger型估计器产生局部状态估计值φj(k)，形式为：

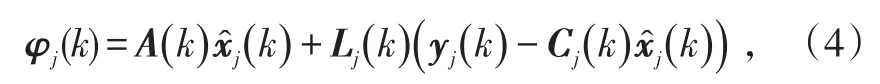
式中，Lj(k)为估计器增益。

Step 2：由于网络延时、网络堵塞、外界干扰等因素影响，传感器节点j向节点i(i≠j)发送局部状态估计值时会出现数据包丢失现象，本文将节点j的局部状态估计丢失现象描述为：

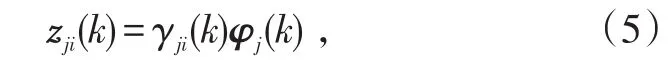
式中，zji(k)表示节点j到达节点i处的信号。

{γji(k)}是满足Bernoulli分布的随机变量序列且不相关于其他变量，其概率分布为：

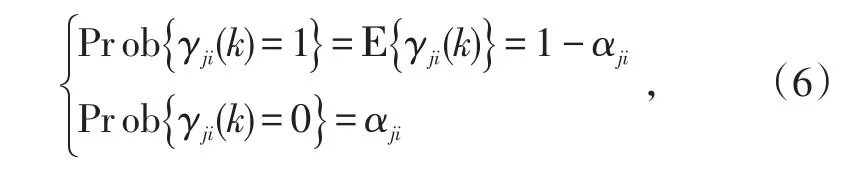
式中，αji表示传感器节点j与i间传输通道的丢包率，满足0＜αji＜1。

当γji(k)=1时，节点j发送到节点i的局部状态估计值没有丢失；γji(k)=0时表示局部状态估计值丢失。为了减少丢包对节点i融合性能的影响，当节点j向节点i传输的局部估计值丢失时，采用上一时刻融合节点i处融合估计值的一步预测值作为补偿，称为重组局部状态估计，记为，计算式为：

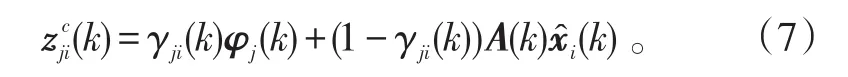
传感器节点i将接收到的全部重组局部状态估计值进行一致性加权融合，得分布式一致性估计值为：

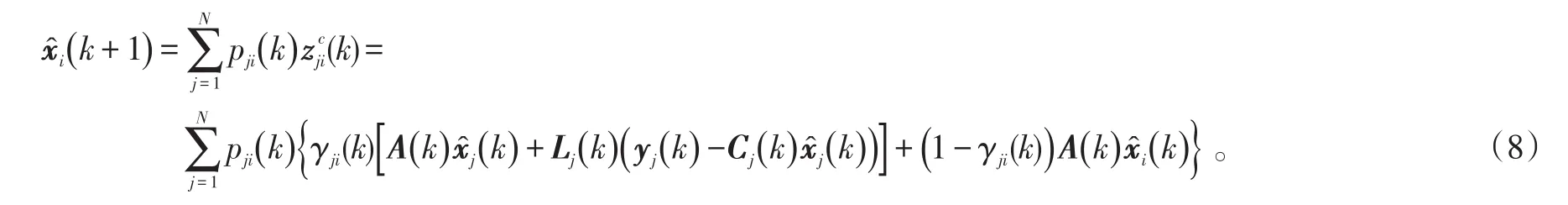
式（8）中，pji(k)=pij(k)表示各节点间的一致性权重，且满足和pji(k)≥0，pji(k)=0表示i和j节点间无通信。

注1：为了表述简单和方便阅读，将下文中不会造成误解和不会影响阅读性的时间标志忽略，例如将A(k)简化为A，Ci(k)简化为Ci等。

设融合节点i的状态估计误差为εi(k)，即

结合式（8）、（9）和（10）可得：

为了对整个分布式估计系统的融合性能进行分析，建立有限时域下分布式一致性状态融合估计代价函数为：

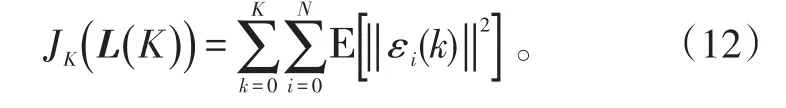
2 次优的分布式一致性估计器设计

在给出主要结论前，首先给出以下引理。

引理1：[16]对于任意正整数N、非负标量组且满足，向量组和矩阵组，则有以下不等式成立：

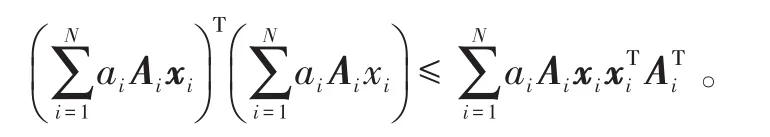
定义k时刻传感器节点i处的状态估计误差协方差矩阵为，结合式（11）得：

式（12）等价于：

从式（13）可以看出，要得到优化问题（14）的最优估计器增益的精确解析式是非常困难的。因此，本文在保证融合性能损失不大的前提下，通过最小化代价函数的上界，得到一组次优的估计器增益。在给出次优解前，首先通过引理2找到代价函数的一个上界。

引理2：考虑如下差分方程：

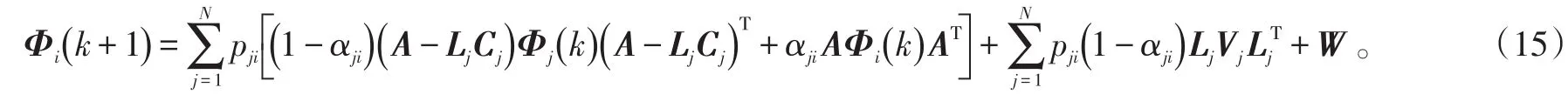
式（15）中，Φi(0)=Pi(0),i=1,2,…,N。

对所有k≥0时，Pi(k)≤Φi(k)恒成立。

证明：

根据引理1并结合式（6）得：

然后，采取数学归纳法证明Pi(k+1)≤Φi(k+1)。

当k=0时，由已知条件得Φi(0)=Pi(0)。

假设k时刻，Pi(k)≤Φi(k) ，则：

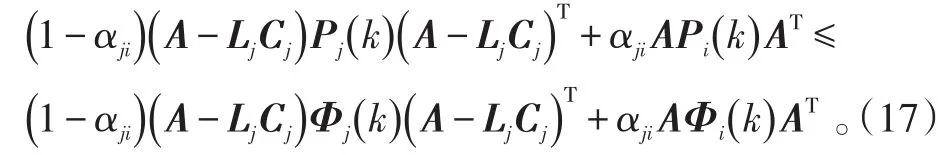
综合式（15）和（17）可得：Pi(k+1)≤Φi(k+1)成立。证毕。

根据引理2得到了融合估计误差协方差矩阵的上界。记Φi(k)为次优矩阵，定义次优代价函数如下：

由引理2可知：

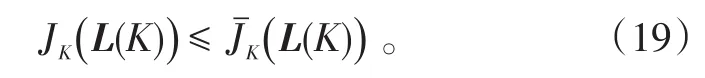
因此，通过求解式（18）便可得到一组次优的估计器增益Lc(K)，即：

根据引理2的结论和分析，以下定理给出优化问题（20）的最优解。

定理1：优化问题（20）的最优解为：次优代价函数(L(K))的最小值为：

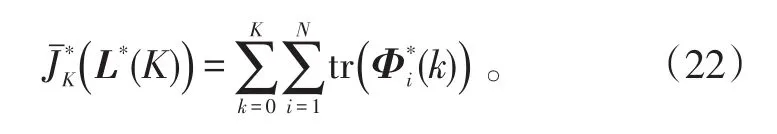
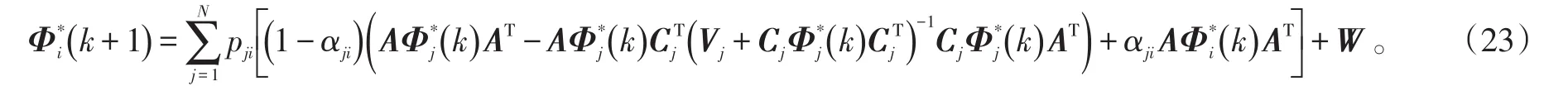
证明：令优化问题（20）的最优解为：

任意一组可行解为：

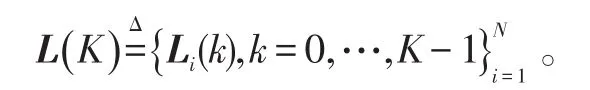
分别将L*(K)和L(K)代入式（15）得到和。

要证式（22）成立，只需证明：

结合式（18）和（22），只需证明：

将式（21）代入式（15）得：

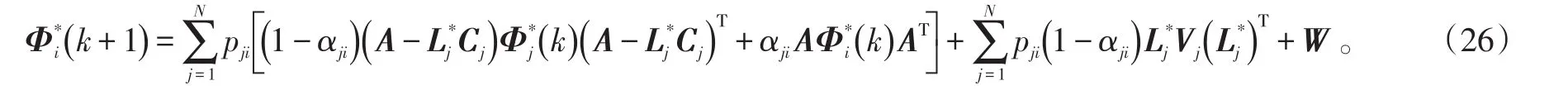
容易证明有以下恒等式成立：

则式（26）变形得到：

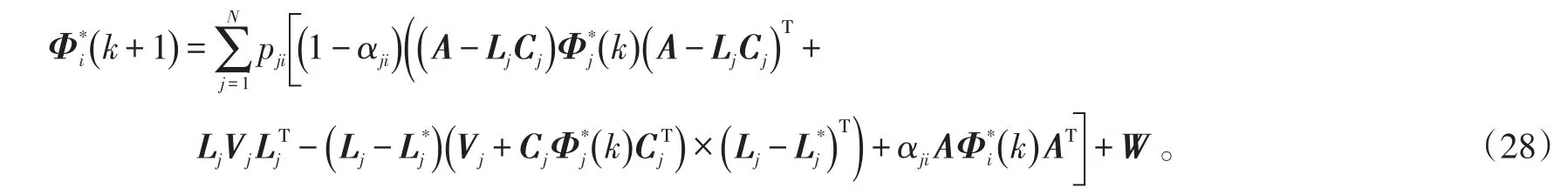
于是得到：

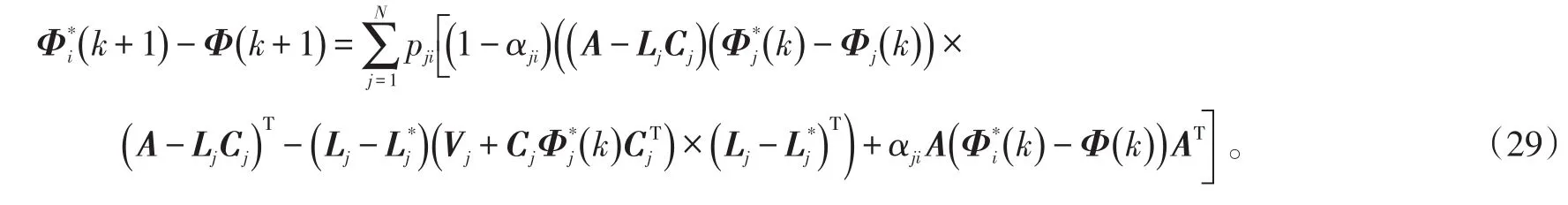
根据数学归纳法，k=0时，由已知条件知式（25）显然成立；假设是正定矩阵，则有：

进一步得到：

将式（26）化简便得到式（23）。证毕。

3 稳定性分析

在证明带丢包的分布式一致性估计算法稳定性之前，给出如下引理：

引理3：[16]对于任意正整数N、非负标量组且满足，向量组和正定矩阵Q，则有以下不等式成立：

定理2：对于给定的一致性权重p(k)，k＞0时，对于正定矩阵组，若存在正定对称矩阵组和增益矩阵组L(K)满足以下等式：

则带丢包的分布式一致性融合状态估计误差εi(k)在无噪声时是渐进稳定的，即。

证明：不考虑随机噪声影响，融合估计误差为：

定义Lyapunov函数：

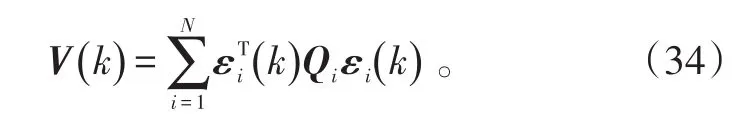
结合式（33）和（34）得：

由引理3和γji(k)的定义可得：

将式（36）交换求和顺序并合并得到：

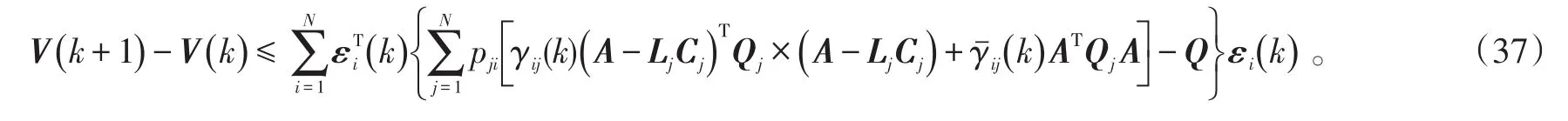
令：

即得到式（32）。

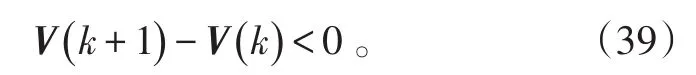
从而由以上分析得到了融合估计误差渐进稳定的充分条件。

证毕。

4 算例仿真

考虑由4个传感器节点组成的分布式一致性状态融合估计问题，其中目标系统方程为：

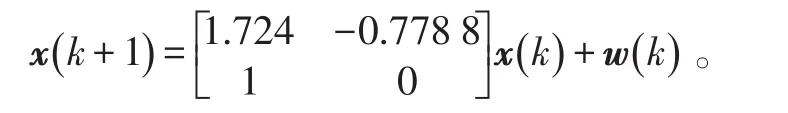
4个传感器的量测方程为：

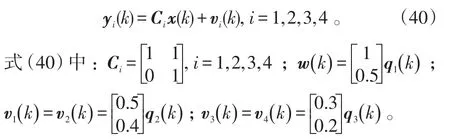
q1(k)、q2(k)和q3(k)是互不相关的零均值白噪声，其协方差分别为0.1、0.2和0.3。各初始值取如下：

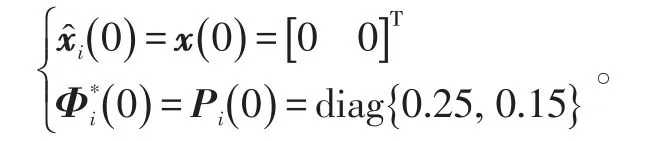
给定一组一致性权重如下：

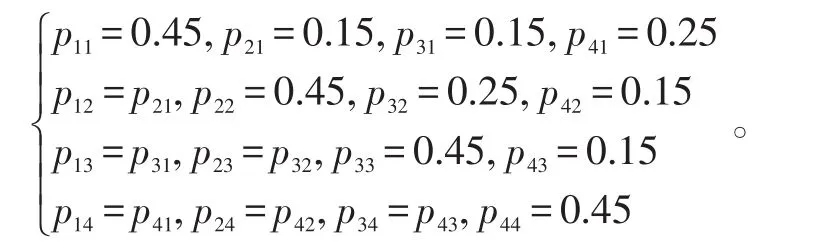
假设各传感器节点间不同传输通道的丢包率为：

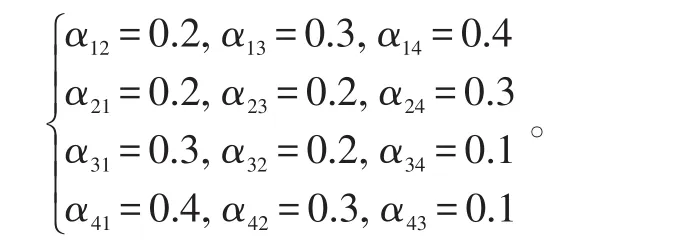
图1给出了当发生丢包时各传感器节点对目标轨迹的跟踪情况。从图1可见，本文所设计的分布式一致性融合估计算法在丢包时仍能很好地估计目标信息，且各节点对目标的估计趋于一致。

图2给出了各传感器节点次优矩阵的迹。从图2可见，各节点次优矩阵的迹是收敛的。根据引理4，各节点融合估计误差协方差的迹也是收敛的，从而验证了定理2的正确性。

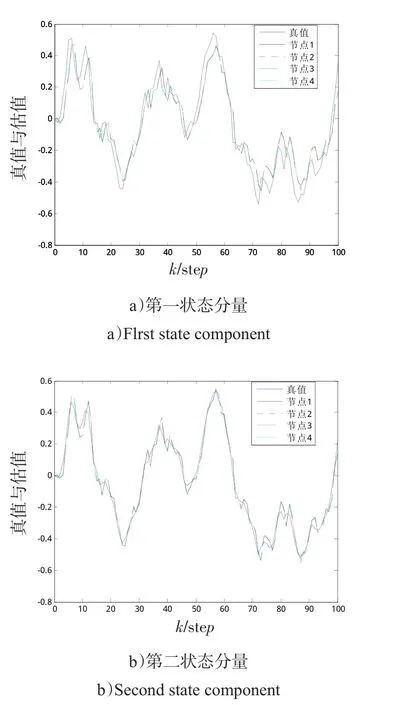
图1 各传感器节点目标轨迹跟踪图Fig.1 Tracking performance of each sensor node

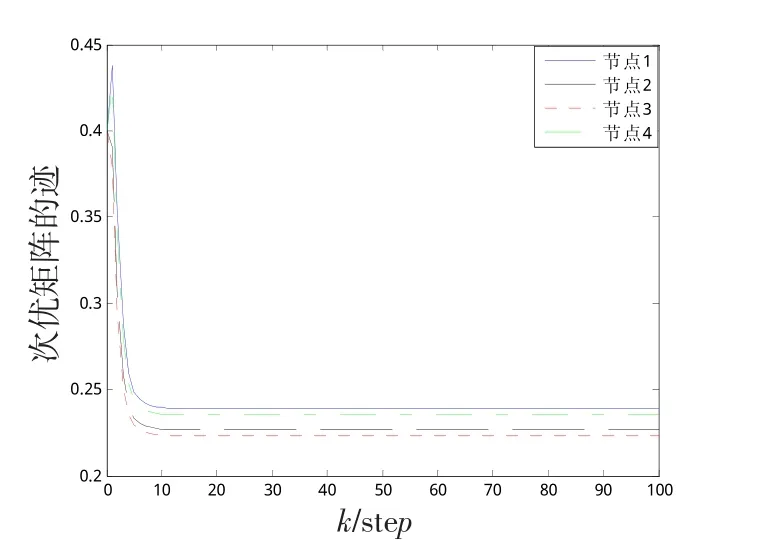
图2 各传感器节点次优矩阵的迹Fig.2 Traces of sub-optimal matrices for each sensor node

定义系统的平均估计误差和非一致性平均估计误差为：

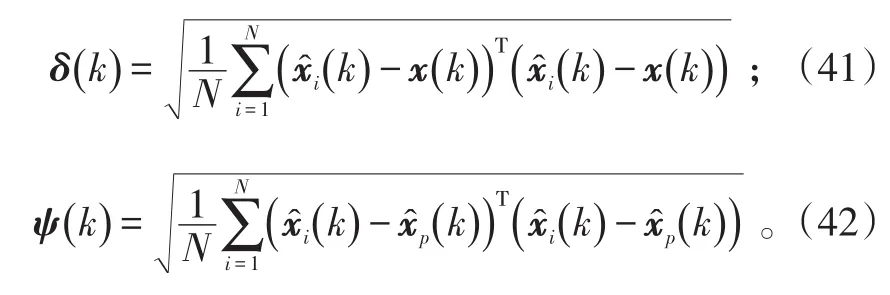
图3给出了带补偿和无补偿下的估计误差对比。从图3可见，带有补偿的估计精度和一致性都比无补偿的估计精度和一致性高。从而说明本文采用的丢包补偿方法能够改善各传感器节点对目标状态估计的估计精度，增强估计的一致性。

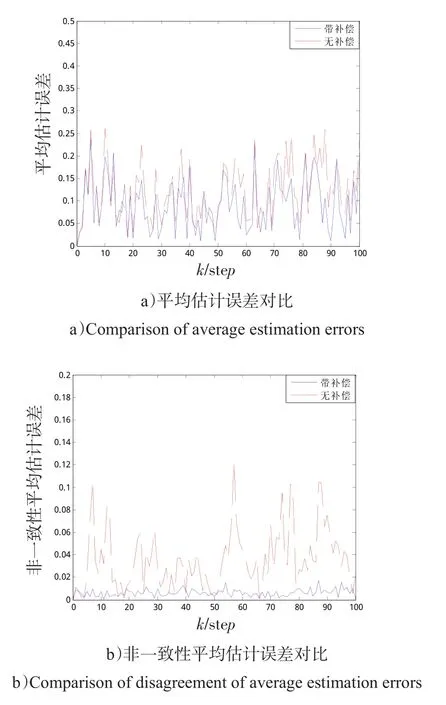
图3 带补偿和无补偿的估计误差对比Fig.3 Estimated error comparison with compensation and no compensation

5 结论

本文研究了具有局部状态估计值丢失的网络化多传感器分布式一致性融合估计问题。在各传感器节点融合端建立了具有补偿的随机丢包模型。为了简化问题，利用不等式理论得到了一组次优估计器增益，并基于Lyapunov稳定性方法得到了估计器渐进稳定的充分条件。仿真结果表明，本文所设计的算法能够有效降低局部状态估计值丢失对融合性能的影响；同时也表明当发生丢包时采用补偿比没有补偿具有更高的估计精度和更好的一致性。