俯冲拉起飞行条件下航空发动机整机动力学特性分析

秦海勤，王 昊，徐可君，张耀涛

（1.海军航空大学青岛校区，山东青岛266041；2.青岛科技大学机电工程学院，山东青岛266061）

飞机机动飞行时，发动机转静子系统均会产生附加载荷，附加载荷的存在一定程度会使得发动机转子系统的振动特性发生改变，甚至引起振动失稳，导致等级事故。飞行实践也一再表明，机动飞行时，飞机发生事故的概率明显增加。而现代战争的发展对飞机的机动性提出了更高要求。因此，为保证飞行安全，促进发动机振动实测、结构设计、安装方式的改进等，有必要进一步揭示俯冲拉起等机动飞行条件下航空发动机的整机动力学特性变化规律。

Geradin与Kill[1]是最早开展机动飞行对发动机动力学特性影响研究的学者之一，他们提出了一种考虑机动飞行对发动机动力学特性影响的分析方法。White等[2]在飞行试验中观察了机动飞行对发动机转子工作的影响。祝长生与陈拥军[3-4]建立了飞机在作任意机动飞行条件下多盘、多集中质量和多轴承的不平衡柔性转子系统的运动模型。徐敏与廖明夫[5-6]建立了飞机作水平盘旋和俯冲拉起两种机动飞行条件下双盘悬臂转子系统的运动微分方程，并建立了支承在挤压油膜阻尼器下Jeffcott转子的运动微分方程。林富生与孟光[7]研究了恒定角速度与恒定加速度机动飞行对Jeffcott转子系统的动力学特性影响。魏海涛等[8]研究了机动飞行对双转子系统的动力学特性影响。张群岩等[9]利用某型发动机的试飞数据验证了机动飞行条件下发动机转子振动特性的一般性。杨永锋等[10]研究了水平盘旋下裂纹转子的非线性响应。白雪川[11]分析了机动飞行下双转子系统的动力学响应特性。于渊博[12]建立了有机动附加载荷下非线性弹性裂纹转子系统的数学模型，对转子在机动飞行中的振动特性进行了仿真。侯磊[13]通过仿真试验，得出了非线性弹性支承下转子系统在Herbst机动飞行环境下的振动响应。杨蛟[14]设计开发了可模拟机动飞行的双转子模型试验台。

然而，国内外学者对于机动飞行对航空发动机动力学特性的影响研究大都基于Jeffcott转子或简单的双转子系统，并没有考虑带机匣的复杂双转子系统，且附加载荷均加在圆盘上，而飞机在实际机动飞行过程中机匣与转子都会发生振动，且附加作用力会通过支承在转静子间相互传递。因此，机动飞行时转子和静子机匣具有极强的耦合性。本文在前人研究的基础上，开展俯冲拉起飞行条件下带有机匣的整机动力学响应特性研究及机匣支承和安装节支承对整机动力学响应特性的影响研究。

1 双转子航空发动机整机动力学建模

1.1 系统模型建立

航空发动机结构复杂，建立真实的发动机模型异常困难。本文以图1中航空发动机整机动力学特性试验器为参考，建立发动机双转子-支承-机匣耦合动力学模型，如图2所示。为便于观察和描述机匣的支撑情况，图2为试验器水平剖面的示意图。该模型的转子系统由风扇转子、高压转子和低压转子3个转子组成。其中，风扇转子与低压转子通过套齿联轴器I连接，高压转子与低压转子在D位置通过中介轴承连接。转子分别在A、B、C、E位置通过轴承-弹性支承与机匣连接（称为机匣支承）。机匣通过弹性支承与基础连接（称为安装节支承）。

图1 航空发动机整机动力学特性试验器Fig.1 Dynamic characteristics of dual-rotor aero-engine experimental apparatus

图2 航空发动机双转子-支承-机匣耦合动力学模型Fig.2 Dual rotor-bearing-casing coupling dynamic model

1.2 系统有限元模型建立及验证

将图2中的双转子-支承-机匣耦合动力学模型简化为图3中的整机系统有限元模型。其中，转子轴的有限元建模方法采用Timoshenko梁理论[15-18]。

为简化计算，将套齿联轴器对应轴段考虑为梁单元计算。在机匣的有限元建模上，国内外学者大都把机匣看作转速为零的梁元素，而在实际中，机匣的厚度为1～2mm，振动时会产生周向变形，而梁元素法并未考虑周向变形，因而在用梁元素法对机匣进行有限元建模时会产生较大误差[17]。为此，本文采用截锥壳法对机匣进行建模，将机匣简化为有限个锥壳单元的组合。

图3 整机系统有限元模型Fig.3 Dual rotor-bearing-casing coupling finite element model

试验器采用挤压油膜轴承。经测试，轴承的横向支承阻尼CH与垂向支承阻尼CV约为20 N⋅s/m。机匣支承刚度K1～K5约为5×107N/m。由于安装节支承刚度K6、K7与其安装条件密切相关，实测难度较大。本试验器安装节与机匣采用了相同的材料，故将支承刚度K6、K7也近似取为5×107N/m。根据该实验器的实际工作转速范围，参考目前主流发动机高低压转子系统反向旋转的客观事实。在分析过程中，令高压转子转速为9 000 r/min，低压转子反向旋转，两者转速比为-1.5，即低压转速为6 000 r/min。当机匣与双转子系统耦合时，周向波数取1。其他相关计算初始参数见表1～4。

表1 转子主要计算参数Tab.1 Main parameters of rotor

表2 轴承支承参数Tab.2 Parameters of bearing

表3 转子-转子中介轴承支承参数Tab.3 Parameters of intermediate bearing

表4 机匣主要计算参数Tab.4 Parameters of casing

为验证所建立模型的准确性，理论计算了试验器整机系统的临界转速，并与实际测试结果进行了对比。由于双转子系统的临界转速受高低压转子转速的双重影响，较为复杂。为便于比较，在理论计算和实际测试时固定其中一根转子，让另一根转子旋转。图4～5分别为低压转子为主激励时（高压转子转速为0）理论计算的坎贝尔图和实际测试的伯德图。

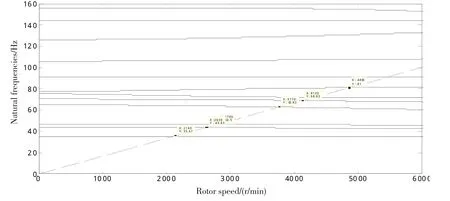
图4 理论计算低压转子为主激励时坎贝尔图Fig.4 Campbell diagram for low pressure rotor excitation based calculation

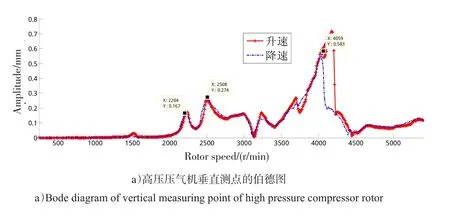
图5 实测低压转子为主激励时（高压转子转速为0）各测点的伯德图Fig.5 Bode diagram of measurement points for low pressure rotor excitation based testing

从坎贝尔图和伯德图可找到系统此时的计算和实测临界转速（由于实测过程中升、降速的差异，一般均通过降速过程的伯德图查找临界转速，故本文也遵循这一原则）。与此类似，可进一步对比高压转子为主激励时系统的临界转速，所得结果如表5所示。表5中：相对误差=100×|实测值-计算值|/实测值。

表5 计算与实测临界转速对比Tab.5 Calculated and measured critical speed

对比表5中数据可知，由于建模过程中的简化（如将套齿联轴器连接处视为连续轴段）和安装节支承刚度的选取，使得理论计算与实际测试结果存在一定误差（相对误差不超过6%），综合考虑测试过程中的随机误差等，本文认为所建立有限元模型有效。

2 俯冲拉起机动飞行条件下双转子航空发动机整机动力学分析

飞机实际飞行过程中，会包括各种飞行剖面。对于作盘旋和俯冲动作的飞行剖面，一般会经历这样的阶段，即滑跑（1-2）起飞（2-3）—水平盘旋（3-4）—俯冲拉起（4-5）—降落（5-6），见图6。本文选取俯冲拉起机动飞行作为研究对象。

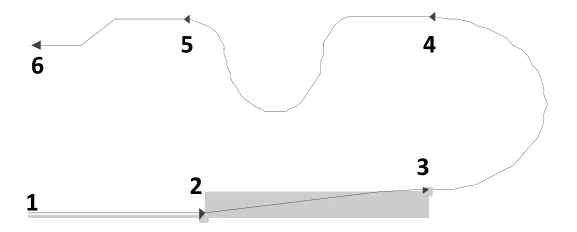
图6 飞机机动飞行轨迹图Fig.6 Maneuver flight trajectory

为突出研究的主要内容，忽略气动方面和重力的影响。在以上假设下，根据上述有限元模型，建立了航空发动机整机动力学方程为：++Ku=Q。其中：M为包括机匣和转子在内的质量矩阵；C为阻尼矩阵；K为刚度矩阵；Q为外部作用广义力向量；u=[x,y,θx,θy]T，其中，x为水平方向位移，y为竖直方向位移，θx为水平方向转角，θy为竖直方向转角。

飞机在做机动飞行时，发动机静子机匣会产生外部附加离心力，而转子系统因高速旋转除会产生附加离心力还会产生附加陀螺力矩。设机动飞行时飞机的飞行速度为V，俯冲拉起角速度为Ω，第i个机匣单元的质量为mC,i，则该机匣单元所受的附加离心力为Fi=[0,-mC,iΩV,0,0]T。对转子系统，与圆盘比各转子轴单元质量较小，故忽略转子轴的质量，只考虑作用在转子系统每个圆盘上的外部离心力和附加陀螺力矩。设mD,j为第j个圆盘质量，Ω为飞机俯冲拉起角速度，V为飞机飞行速度，JP,j为第j个圆盘的极转动惯量，ω为圆盘所在转子轴的角速度，则作用在该圆盘上的附加离心力Fj1=[0,-mD,jΩV,0,0]T，附加陀螺力矩Fj2=[0,0,0,-JP,jΩV]T，将两者综合得作用在该圆盘上的外部作用力为Fj=[0,-mD,jΩV,0,-JP,jωΩ]T。若该圆盘存在质量偏心，则在旋转过程中，该盘还要受到自身的离心力FDu(t)，FDu(t)=[mD,jeω2cos(ωt+φ),mD,jeω2sin(ωt+φ),0,0]T。其中：e为圆盘偏心距，φ为质心初始相位。将上述外部作用力集成，则得到机动飞行时，航空发动机所受的外部作用广义力向量：

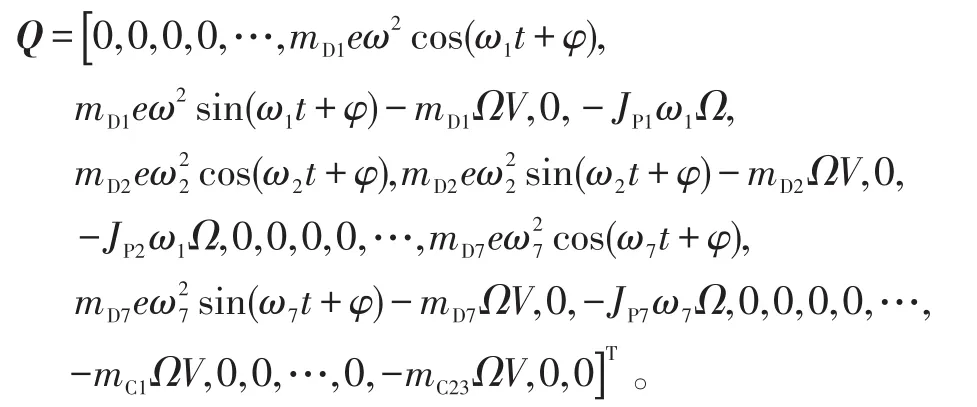
为简化计算，将圆盘偏心产生的不平衡力等效为附加在圆盘上的不平衡质量。假设不平衡力作用在圆盘节点4、12、17上，不平衡质量为m=0.005kg，不平衡质量半径为e=0.2 m，飞机俯冲拉起角速度为0.5rad/s，飞行速度为200 m/s，在飞行过程中，前10 s飞机为水平飞行，10 s后飞机进行俯冲拉起机动飞行。在以上假设条件下，利用所建立模型进行数值计算仿真。为便于比较，以高压圆盘位置节点17与机匣相对应的位置节点33为测点，整个飞行中转子与机匣的轴心轨迹及其所在节点Y方向的时域波形见图7、8，可看出在飞机机动飞行时，转子的轴心和机匣的轴心均会发生偏移，且转子的轴心偏移量明显大于机匣的偏移量。设δ为叶片与机匣之间的间隙，Y1为飞机做机动飞行时转子轴心位移，Y2为机匣轴心位移，当δ＜|Y1-Y2|时，发动机会发生碰摩故障引发事故。

分别将平飞时与俯冲拉起时的时域波形放大，如图9、10、13、14所示，并计算得到测点的频谱图，如图11、12、15、16所示，图中N1为低压转子工频、N2为高压转子工频。对比分析频谱图11、12、15、16，可以看出俯冲拉起机动飞行时转子测点的各转子工频幅值均减小，而机匣测点的各转子工频振幅增大，尤以低压转子工频增大较为明显。对于真实的航空发动机而言，大多通过机匣拾振。因此机匣振动增大，一定程度能够反映机动载荷的影响。

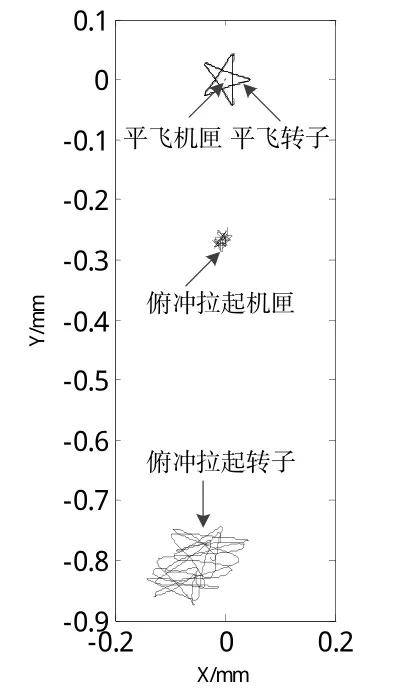
图7 轴心轨迹图Fig.7 Orbit

图8 转子与机匣Y方向的时域波形Fig.8 Time domain waveform of rotor and casing in directionY

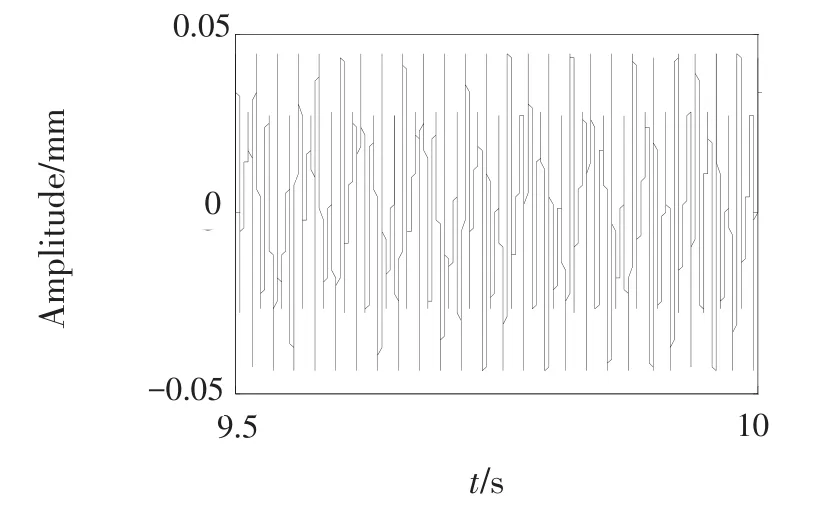
图9 平飞时节点17Y方向的时域波形Fig.9 Time domain waveform of node 17 in level flight in directionY

图10 俯冲拉起机动飞行时节点17Y方向的时域波形Fig.10 Time domain waveform of node 17 in dive maneuvering flight in directionY

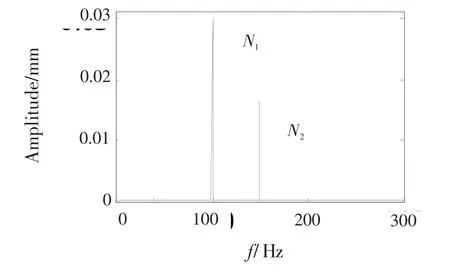
图11 平飞时节点17Y方向的频谱Fig.11 Frequency spectrum of node 17 in level flight in directionY

图12 俯冲拉起机动飞行时节点17Y方向的频谱Fig.12 Frequency spectrum of node 17 in dive maneuvering flight in directionY

图13 平飞时节点33Y方向的时域波形Fig.13 Time domain waveform of node 33 in level flight in directionY

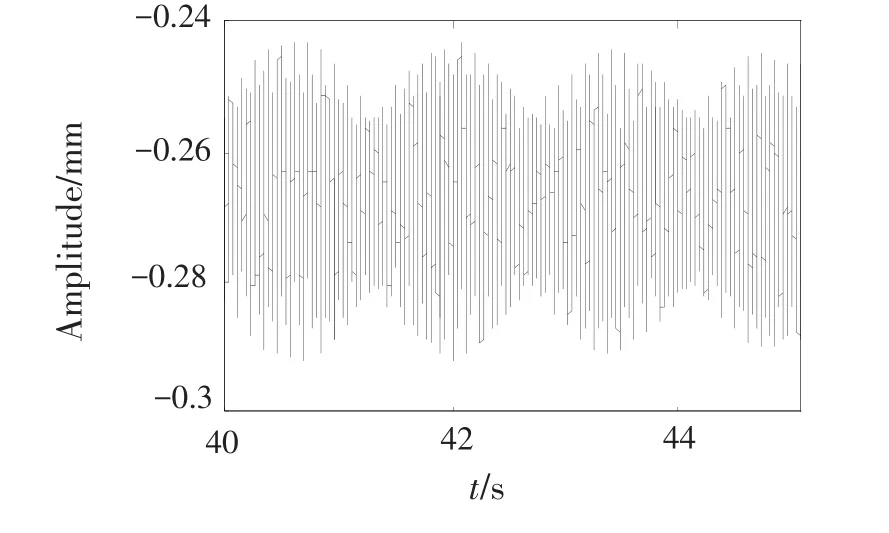
图14 俯冲拉起机动飞行时节点33Y方向的时域波形Fig.14 Time domain waveform of node 33 in dive maneuvering flight in directionY

图15 平飞时节点33Y方向的频谱Fig.15 Frequency spectrum of node 33 in level flight in directionY

图16 俯冲拉起机动飞行时节点33Y方向的频谱Fig.16 Frequency spectrum of node 33 in dive maneuvering flight in directionY

为研究机匣支承刚度对俯冲拉起机动飞行下发动机整机振动的影响，减小机匣支承刚度K1～K5到2×107N/m，安装节支承刚度K6与K7保持不变。仿真计算得到节点17与节点33Y方向上的时域波形与频谱分布，见图18～21。与上文对比发现转子在Y方向上的轴心偏移量明显增大，而机匣的轴心偏移量没有明显变化（图17）。故机匣支承刚度减小引起发动机产生碰摩故障的可能性进一步增大。但分析此时转子与机匣各测点的频谱图，见图19、21，发现转子的振幅虽有所增大，但机匣的振幅反而减小。故在此情况下，仅通过机匣拾振很难反映出整机的真实振动。

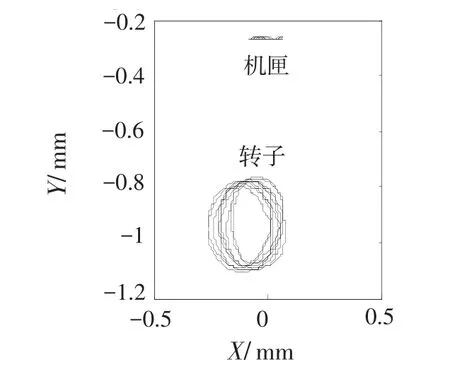
图17 轴心轨迹图Fig.17 Orbit

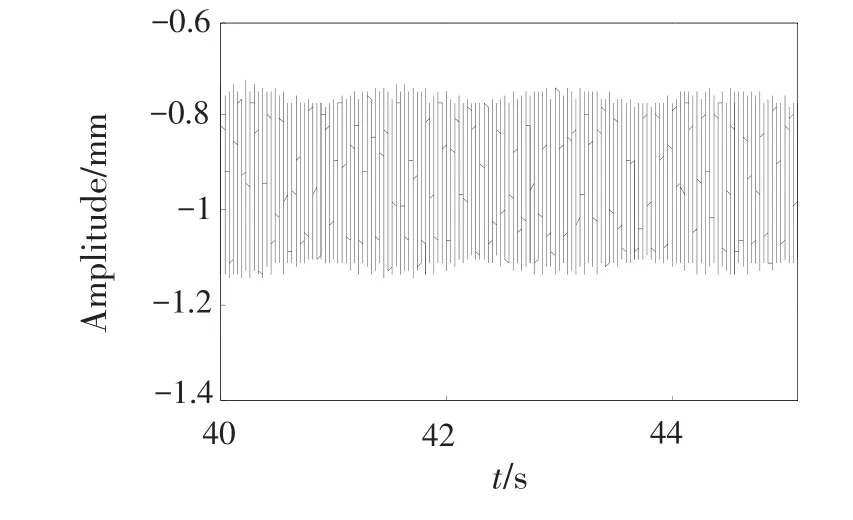
图18 俯冲拉起机动飞行时节点17Y方向的时域波形Fig.18 Time domain waveform of node 17 in dive maneuvering flight in directionY

图19 俯冲拉起机动飞行时节点17Y方向的频谱Fig.19 Frequency spectrum of node 17 in dive maneuvering flight in directionY

图20 俯冲拉起机动飞行时节点33Y方向的时域波形Fig.20 Time domain waveform of node 33 in dive maneuvering flight in directionY

图21 俯冲拉起机动飞行时节点33Y方向的频谱Fig.21 Frequency spectrum of node 33 in dive maneuvering flight in directionY

假设机匣支承刚度K1～K5不变，安装节支承刚度K6与K7减小到2×107N/m，仿真计算得到节点17与节点33的轴心轨迹（如图22所示）及各测点Y方向上的时域波形（如图23、25、26所示）。

研究发现转子与机匣的轴心轨迹及其在Y方向上的偏移量都明显增大。由于两者增大的幅度几乎相同，其差值保持不变。故从引发碰摩故障角度而言，安装节支承刚度影响不大。但安装节支承刚度减小，机匣测点的各转子工频幅值明显增大，不利于发动机的正常工作。

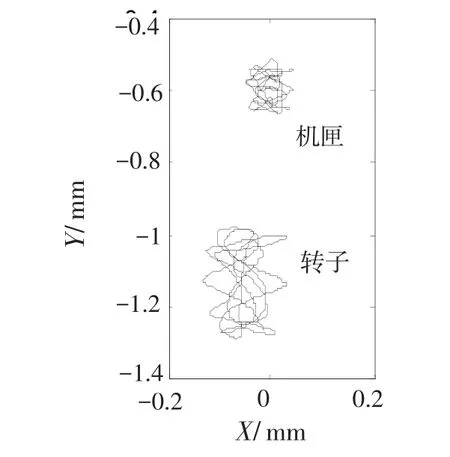
图22 轴心轨迹图Fig.22 Orbit

图23 俯冲拉起机动飞行时节点17Y方向的时域波形Fig.23 Time domain waveform of node 17 in dive maneuvering flight in directionY

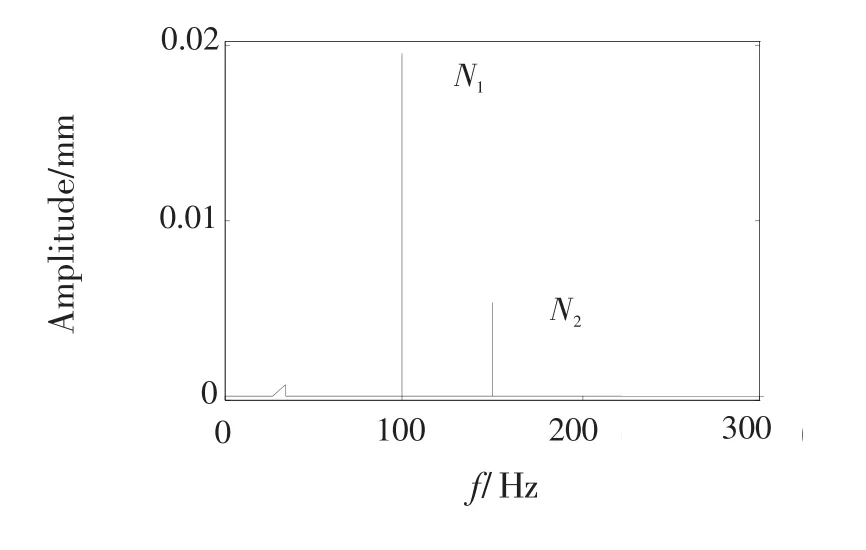
图24 俯冲拉起机动飞行时节点17Y方向的频谱Fig.24 Frequency spectrum of node 17 in dive maneuvering flight directionY

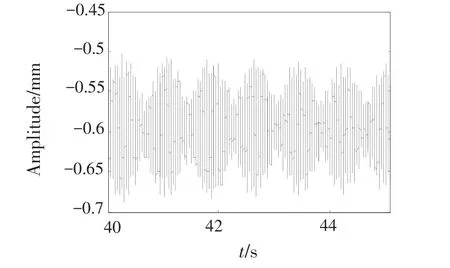
图25 俯冲拉起机动飞行时节点33Y方向的时域波形Fig.25 Time domain waveform of node 33 in dive maneuvering flight in directionY

图26 俯冲拉起机动飞行时节点33Y方向的频谱Fig.26 Frequency spectrum of node 33 in dive maneuvering flight in directionY

假设机匣支承刚度与安装节支承刚度保持不变，俯冲拉起角速度增大为1.0rad/s。仿真计算得到节点17与节点33轴心轨迹（如图27所示）和Y方向上的时域波形（如图28、30所示）。

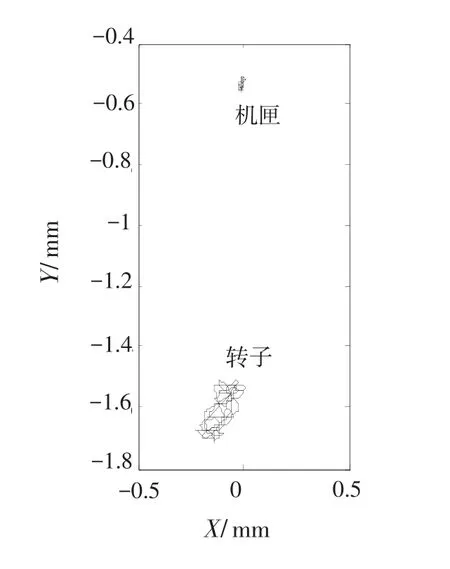
图27 轴心轨迹图Fig.27 Orbit

将图28、30与图10、14比较发现转子与机匣在Y方向上的轴心偏移量均增大，且两者的增大幅度不同。转子的增大幅度明显大于机匣的增大幅度。因此，当机动载荷增加时，转静子之间的径向间隙减小，发动机产生碰摩的可能性增大。

对比分析此时的转子与机匣测点频谱图（图29、31所示）与图12和图16对应的频谱图，发现机动载荷增加时各转子工频N1和N2的振幅基本不变。说明机匣拾振虽然一定程度能够反映机动载荷的影响，但对俯冲拉起机动载荷的变化不敏感。

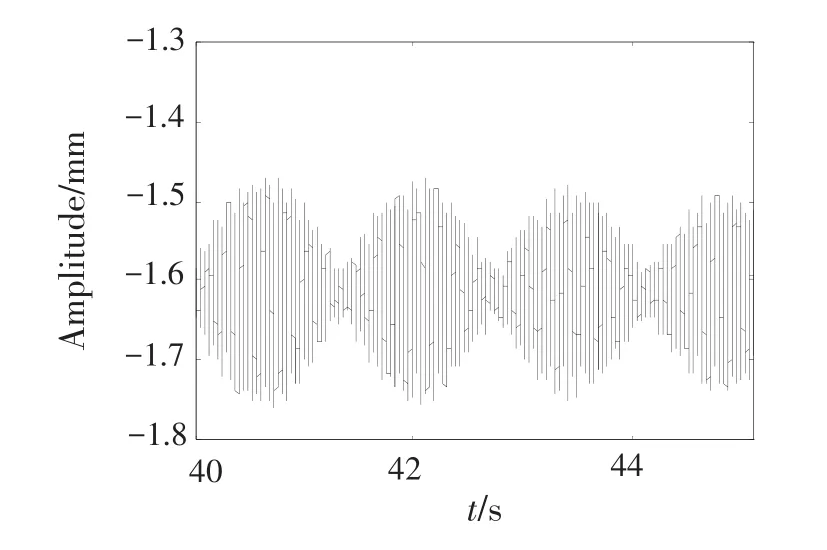
图28 俯冲拉起机动飞行时节点17Y方向的时域波形Fig.28 Time domain waveform of node 17 in dive maneuvering flight in directionY

图29 俯冲拉起机动飞行时节点17Y方向的频谱Fig.29 Frequency spectrum of node 17 in dive maneuvering flight in directionY

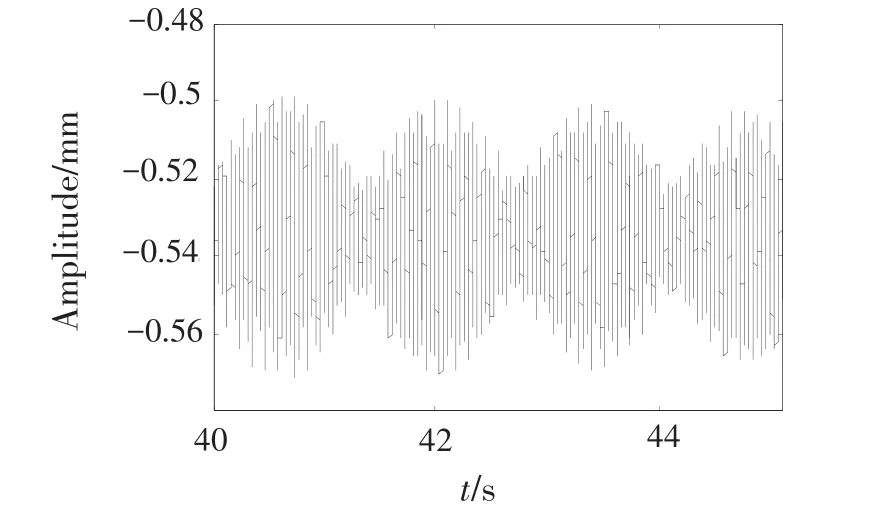
图30 俯冲拉起机动飞行时节点33Y方向的时域波形Fig.30 Time domain waveform of node 33 in dive maneuvering flight in directionY

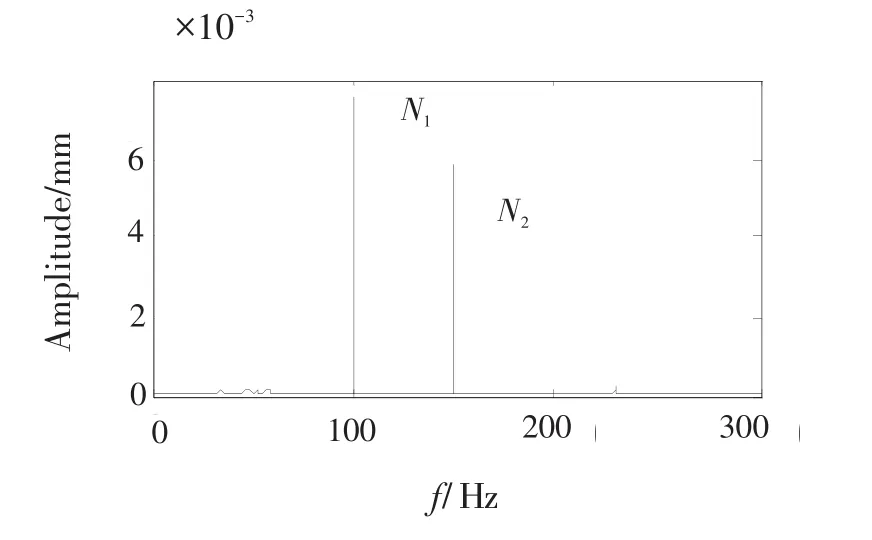
图31 俯冲拉起机动飞行时节点33Y方向的频谱Fig.31 Frequency spectrum of node 33 in dive maneuvering flight in directionY

3 结论

研究俯冲拉起等机动飞行条件下，转静子的振动响应及各支承刚度对整机振动的影响，无论对外场使用发动机振动监控还是发动机整机振动优化均具有一定的工程指导意义。本文计算仿真研究得到：

1）机动载荷对发动机转静间发生径向碰摩的影响较大。当俯冲拉起角速度增大时（由0.5rad/s增加到1.0rad/s），转子的轴心偏移增量明显大于静子的轴心偏移增量，从而使发动机发生转静子间径向碰摩的概率大大增加。但机匣测点振动对俯冲拉起机动载荷的变化不敏感。

2）机匣支承刚度对发动机发生碰摩的影响较大，机匣支承刚度过小引起转静子间径向碰摩的可能性增加，而机匣测点的振动值随机匣支承刚度的减小而减小。

3）安装节支承刚度对发动机发生转静子间径向碰摩的影响相对较小，但安装节支承刚度减小，机匣测点的各转子工频幅值明显增大。