带角度约束的多飞行器编队协同拦截制导律设计

王利国，马国欣，矫永康

（1.北京青云航空仪表有限公司，北京顺义101300；2.烟台大学计算机与控制工程学院，山东烟台264001；3.海军航空大学，山东烟台264001）

新的作战需求和目标特性（如较高的速度、较强的机动能力）给拦截制导系统的设计带来新的挑战。针对此类问题，研究者在传统制导律设计的基础上，提出了很多新的拦截制导方法，如最优制导[1]、微分对策[2]、模糊变结构[3]、滑模制导[4]、微分几何[5]及改进的比例导引[6]等方式。从体系对抗的角度来看，上述制导律的设计实施的是“一对一”的对抗策略。然而，在复杂环境下，随着目标智能化程度愈来愈高，即使将单个飞行器的对抗性能发挥至极致，其探测能力和拦截能力也难以满足高精度、高拦截概率的需求[7]。

在制导拦截过程中，采用多飞行器协同拦截的方案逐渐受到研究者的关注。多导弹编队协同拦截，一方面可以通过飞行器间的信息共享完成对同一目标的协同探测，从而提高目标运动信息的测量精度[8-10]；另一方面，可以通过协同制导律的设计，以特定的编队构型完成对同一目标的协同拦截，以扩大拦截区域的方式弥补单枚导弹对抗测量信息不准确及目标机动时的不足[11]。

目前，关于协同制导的研究多见于多飞行器对固定目标或慢速移动目标的协同攻击[12-16]，此类研究中的制导律不能适用于目标高速运动的情况。Vermeulen A[11]等人证明了采用“二对一”的协同对抗策略能够扩大拦截区域从而提高对运动目标的拦截概率，但并未探讨协同拦截制导如何实现的问题。Piet-Lahanier H等人[17]采用预测控制的方法，设计了考虑攻击同一目标时多枚导弹之间相互避碰的制导律。Shaferman V等人采用最优控制的方法设计了带有指定角度约束的拦截制导律，通过为编队中的导弹指定预设的拦截角度，多枚导弹能够以特定的角度构型拦截目标[18]；之后，又通过不指定每枚导弹的具体拦截角度，而是控制编队中导弹的相对拦截角度的方法实现了编队的角度构型[19]。文献[17-19]对拦截制导的研究，均未考虑对导弹飞行时间的控制调整，而实际上由于不同的发射时间、发射地点（或中段制导结束时不同的导弹位置）、飞行速度、飞行轨迹等多种因素的影响，编队中的各导弹到达拦截点或拦截区域的时间差较大，严重影响了协同拦截的实现。文献[20-22]在导弹径向速度完全受控的假设下，设计了未考虑角度约束的协同制导律。此类制导律以径向速度大小为协调变量，实质上是仿照了无人机的制导方式（速度可任意增减），且文献[21-22]的本质是追踪导引法，这对于拦截高速运动目标是不利的。

考虑到飞行器在径向方向实现自由加减速是困难的，本文在传统的飞行器径向速度不受控的基础上，重点围绕飞行器编队的时间协同展开。首先，在初始时刻，按照各飞行器拦截时间差最小及编队整体拦截时间最小的策略为各飞行器分配预设的拦截角度。然后，利用最优控制求解飞行器以分配的角度拦截目标的导引指令，并给出飞行器剩余飞行时间的求解方法。最后，根据剩余时间一致性的原则，推导出各飞行器时间调整项的导引指令。仿真表明，提出的协同拦截制导方法能够实现飞行器编队以特定的角度构型对目标协同拦截。

1 问题的描述

由n枚弹组成的飞行器编队对同一目标的拦截制导关系如图1所示。

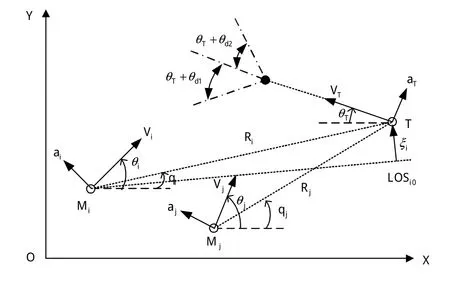
图1 多飞行器协同拦截示意Fig.1 Cooperative interception geometry for multi-aircrafts

图1中：下标i、j、T分别代表第i枚飞行器、第j枚飞行器和目标，i,j∈{1,2,…,n}；速度、法向加速度、航向角分别表示为V、a、θ；R、q分别表示惯性坐标系下的弹目距离、目标视线角；期望的终端拦截角度为θd1+θT，θd2+θT，…，θdn+θT；LOSi0代表初始视线方向，目标在垂直于此方向上的相对位移表示为ξ。

目标与飞行器在此方向上的加速度分量表示为：

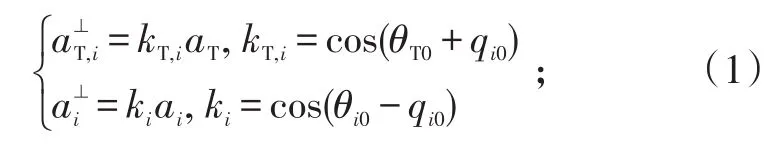
第i枚飞行器与目标的相对运动方程为：

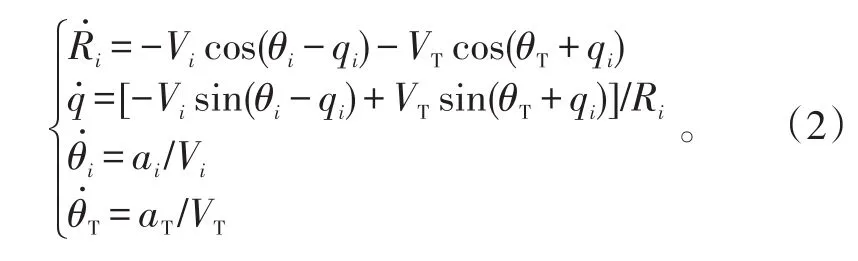
用ui表示导引指令，假定飞行器的侧向机动具有理想动态，有

将导引指令ui分解为两部分：

式（4）中：uA,i引导飞行器以分配的拦截角度攻击目标；uB,i用于调整飞行器的剩余飞行时间。

2 协同拦截制导律设计

2.1 拦截角度分配策略

直接为飞行器M1、M2、…、Mn分别指定终端拦截角度θd1+θT、θd2+θT、…、θdn+θT，可以获得期望的终端角度构型。然而，该方法没有进行系统优化，可能造成不必要的能量损耗。

为使各飞行器能够择优选取终端拦截角度，需要按照一定的策略为飞行器分配拦截角度，即对于飞行器编队{M1、M2、…、Mn}，及其需要实现的终端拦截角度集{θd1+θT、θd2+θT、…、θdn+θT}，寻求一组对应关系，使得终端拦截角度的分配满足某种最优指标。

为建立拦截角度分配问题的数学模型，用Pi,j表示决策变量，当第i枚飞行器分配到第j个终端拦截角度时，Pi,j=1，否则Pi,j=0。用Ci,j表示第i枚飞行器以第j个终端拦截角度导向目标时，其初始剩余时间估计值。为有效实施多飞行器协同拦截制导，对于终端角度的分配，优化指标需考虑2个方面：一是期望各飞行器的飞行时间差较小，二是期望飞行器编队的整体拦截时间较小。因此，考虑时间协同的拦截角度分配问题的优化模型描述为：

该问题属于数学中的整数规划问题，采用规划算法可以得出问题的解。ω代表优化指标2个方面的权重。注意到，ω=1时，该问题退化为典型的目标分配问题。对于剩余时间估计值的解算见2.3节。

2.2 导引指令uA,i的解算

假定拦截过程中飞行器与目标偏离初始视线的角度较小，在此基础上可采用线性化的方法推导导引指令uA,i。注意到，若初始时刻该小角度假设不能满足，或飞行器与目标相对于初始视线有较大机动时，则可以采用扩展的线性化方法或Riccati方程等处理方法。

第i枚飞行器的状态向量表示为：

那么第i枚飞行器的线性化方程为：

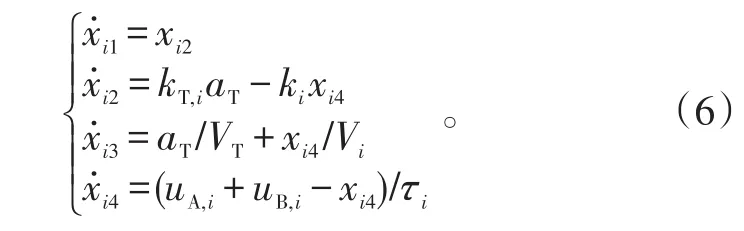
性能指标选取为：

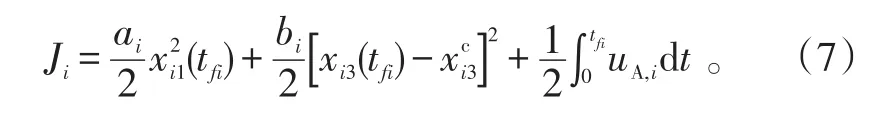
采用最优控制理论求解，最终得到带有拦截角度约束的最优导引指令为：

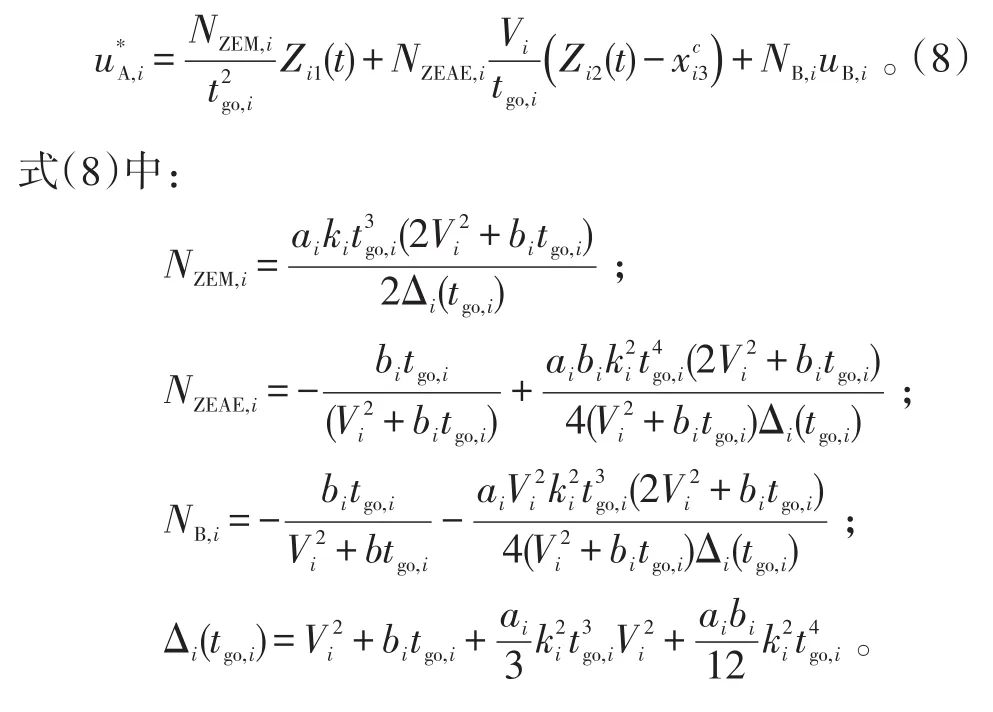
注意到当uB,i=0时，即对编队中各飞行器的剩余飞行时间不进行控制调整，式（8）退化为文献[18]给出的带终端拦截角度约束的最优制导律；当bi→0时，NZEAE,i→0，即终端拦截角度不再受控，若ai→∞则NZEM,i→3/ki，式（8）退化为APN导引律。

Zi1(t)代表零能脱靶量（zero-effort miss），Zi2(t)代表零能拦截角（zero-effort angle），有

2.3 剩余时间估计及导引指令uB,i的解算

文献[23]采用弹目距离除以平均速度的方式，给出了最优制导情况下带终端攻击角度约束的、针对固定目标的剩余时间估算公式：

下面将该方法推广到针对运动目标的情况。

对于第i枚飞行器，用,T表示飞行器与目标相对运动的平均速度，有

采用泰勒多项式近似处理余弦项，得：

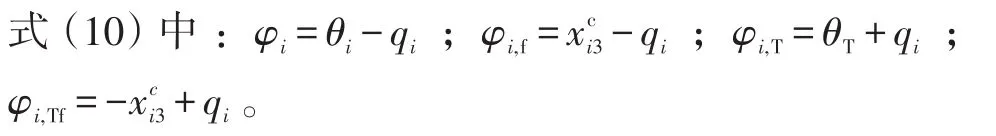
最终可得第i枚飞行器的剩余飞行时间估计值

注意到，利用式（11）求解初始时刻的剩余时间估计，可给出2.1节中所有Ci,j的值。

求解式（11）关于时间的导数，结合式（10）、（2）得：

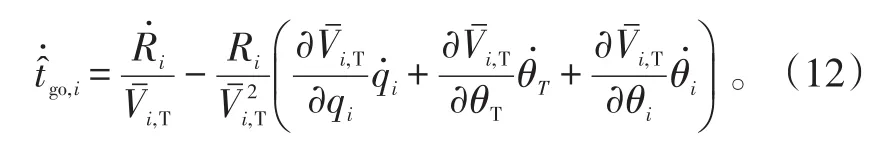
结合式（3）、（4），式（12）可简化为：

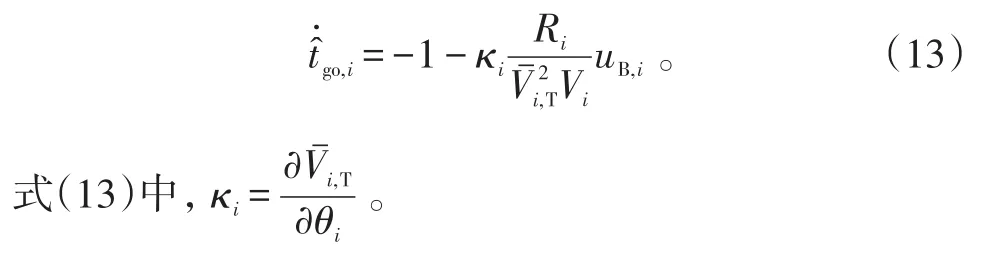
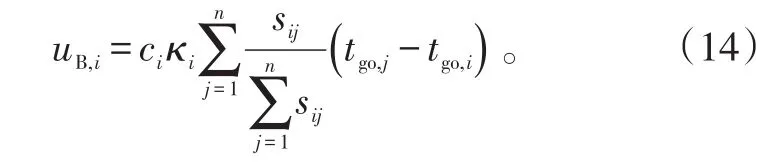
式（14）中，sij为二元函数，反映通信网络的连接情况。

sii≡1；在t时刻，当第j枚弹至第i枚弹存在通信连接时，sij=1，否则sij=0。关于通信网络的研究，文献[24]已进行了重要的探讨，这里不再论述。假定飞行器编队具有全通信，即sij=1，∀i,j∈{1,2,…,n}。

综上，多飞行器协同拦截制导律由式（4）、（8）、（14）给出，编队协同拦截制导框图如图2所示。

图2 多飞行器协同拦截制导Fig.2 Cooperative interception guidance for multi-aircrafts

3 仿真结果与分析

2枚飞行器协同拦截同一目标，目标位于坐标原点(0,0 )，初始航向角0°，速度500 m/s。飞行器M1、M2初始坐标分别为(-5km,0km)、(-6km,0.5km)，初始航向角20°、-30°，M1速度为 500 m/s，M2速度为480 m/s。相对于目标运动方向，期望的拦截角度为20°、-20°。

3.1 对直线运动目标的拦截

对于目标直线运动的情况，若2枚飞行器采用文献[18]给出的带有终端角度约束的最优导引律，仿真结果如图3所示。

文献[18]给出的导引律对剩余飞行时间不进行控制，正如图3b）所示，M1与M2的剩余时间差从制导开始保持到制导结束。

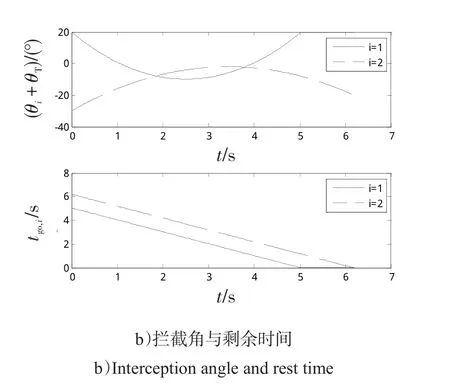
图3 文献[18]的方法对直线运动目标的拦截Fig.3 Interception for the linear movement target by the approach in[18]

飞行器按照指定的拦截角度攻击目标，获得的终端拦截角度分别为19.83°，-19.95°。飞行器M1的拦截时间为5.04 s，飞行器M2的拦截时间为6.20 s，二者相差1.16 s，相当于编队整体作战时间（6.20 s）的18.71%。若不考虑Y方向的速度分量，则2枚飞行器在拦截目标时的相对距离为580 m，这对于编队的整体拦截制导效果是极为不利的。

采用本文给出的协同拦截制导方法：首先，通过式（11）求解初始时刻飞行器编队的剩余时间估计值，得到以Ci,j为元素的2×2矩阵为[5.071 7,6.203 9;]5.051 1,6.277 6，取ω=0.5，得到由Pi,j为元素的2×2矩阵为[0，1；1，0]，即M1分配的拦截角度为 -20°，M2分配的拦截角度为20°；然后，采用设计的多飞行器协同导引律（导引参数取ai=105，bi=108，ci=3×104，i=1,2）。2枚飞行器能够有效地调整剩余时间差，仿真结果如图4所示。最终获得的终端拦截角度分别为-20.20°，19.51°。拦截时间仅相差0.02 s，几乎同时命中目标。

图4 设计的协同制导方法对直线运动目标的拦截Fig.4 Interception for the linear movement target by the designed cooperative guidance approach

3.2 对机动目标的拦截

目标以3 g的侧向加速度机动规避来袭飞行器。飞行器编队采用文献[18]的方法，过载限制为50 g。结果如图5所示。最终获得的拦截角度分别为20.09°、-19.80°，拦截时间分别为5.08 s、6.33 s。显然，由于目标的实时机动，2枚飞行器的拦截时间差进一步增大，达1.25 s。

采用本文给出的协同拦截制导方法（导引参数同上），过载限制为50 g，仿真结果如图6所示。最终获得的拦截角度分别为20.37°、-20.21°，拦截时间分别为6.23 s、6.21 s。

比较图6 a）与图5 a）不难发现，相对于文献[18]对飞行时间不控制的情况，采用协同拦截制导方法后，M1在向目标导引的过程中，通过适度的机动（将其弹道“压得”更加弯曲）调整其剩余时间go,1趋向于go,2，而M2则将其弹道“拉得”更加笔直调整其剩余时间go,2趋向于go,1。当然，相比于飞行时间不控制的情况，这种剩余飞行时间的实时调整，使得过载的需求也变得更大。

图5 文献[18]的方法对机动目标的拦截Fig.5 Interception for the maneuvering target by the approach in[18]

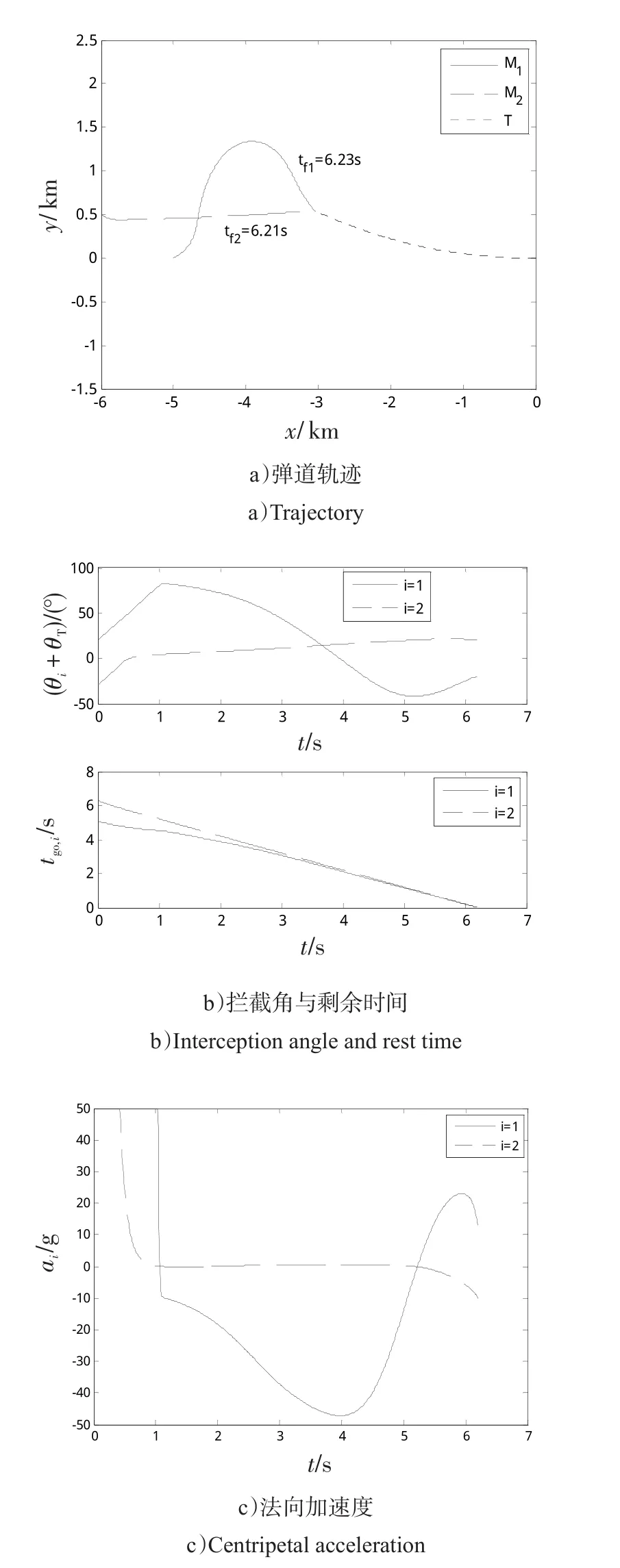
图6 设计的协同制导方法对机动目标的拦截Fig.6 Interception for the maneuvering target by the designed cooperative guidance approach

4 结束语

在初始时刻，以最小化飞行器间的飞行时间差与编队整体飞行时间为指标，建立了拦截角度分配的数学模型。以编队中各飞行器的剩余时间作为协同输出量，通过求解带终端角度约束的导引指令与用于调整剩余时间的导引指令，完成了多飞行器编队协同拦截制导系统的设计。仿真表明，给出的制导方法能够使飞行器编队按照期望的拦截角度协同拦截同一目标。

在多飞行器协同拦截制导过程中，如何避免相互碰撞以及降低因调整飞行器飞行时间对过载的需求是下一步需要重点研究的课题。