跪式起落架结构参数对直升机滚转模态频率影响的研究

宋山松，胡国才，吴 靖

（海军航空大学，山东烟台264001）

直升机地面共振是关系直升机安全的重大问题，必须要在直升机研制设计中设法避免地面共振的发生[1]。目前，国内外对地面共振机理和避免地面共振可采取的措施的研究已经比较深入[2-3]。频率要求是消除直升机地面共振必须满足的设计措施，必须要调节机体在起落架上振动的各阶固有频率，使之与旋翼摆振后退型频率分开，并有足够的转速余量，才能从根本上有效防止地面共振[4]。一般来说，对于铰接式单旋翼直升机，与机体其他模态相比，其滚转模态的惯性矩最小，频率最高，这是影响地面共振最关键的模态[5-6]。起落架构型及布局、起落架刚度和阻尼特性等因素是影响机体在起落架上振动的固有频率的重要因素[7]。若从防止地面共振的角度进行起落架的设计，主要困难之一是保持缓冲支柱所需阻尼定量设计的复杂性[8-9]。因此，起落架参数的确定通常都是在满足直升机着陆载荷要求的基础上，按照地面共振要求进行反复修正得到的[10-12]。通过合理设计起落架结构参数调节机体固有振动频率，把相应的地面共振不稳定区全部移出旋翼最大转速，能够有效防止地面共振。

跪式起落架设计是满足直升机抗坠毁性要求的理想吸能结构，能够最大限度地吸收直升机的坠毁能量，提高乘员生存率，广泛应用于武装直升机和多用途直升机[13-14]。跪式起落架结构参数包括摇臂及缓冲支柱与机身连接点位置、摇臂与机体纵向对称面夹角、缓冲支柱及轮轴长度等参数。若能通过改变跪式起落架结构参数来调节机体滚转模态频率，使之满足地面共振要求，则能节省大量的时间和精力。因此，研究跪式起落架结构参数对直升机滚转模态频率的影响对于改进直升机起落架设计具有十分重要的理论和实践意义。

本文利用缓冲支柱及轮胎的刚度阻尼实验数据，建立了跪式起落架系统等效刚度和等效阻尼的计算模型，分析了跪式起落架结构参数变化对直升机滚转模态频率的影响。

1 地面平衡计算

直升机地面平衡计算的主要目的是为了得到地面载荷（直升机重力与旋翼拉力之差）在主尾起落架上的分布，进而获得直升机在该计算状态下缓冲支柱及轮胎的压缩量等参数[15]。在地面载荷的作用下，采用跪式起落架的直升机轮轴的x向位置将发生变化，因而相对于支柱式起落架直升机而言跪式起落架直升机地面平衡计算也更为复杂。本文采用文献[16]给出的方法计算进行地面平衡计算。

设AC与xoz平面的夹角为θ，BC与xoz平面的夹角为τ，BC在xoy平面的投影与ox轴的夹角为μ。起落架力传递系数分析模型如图1所示。

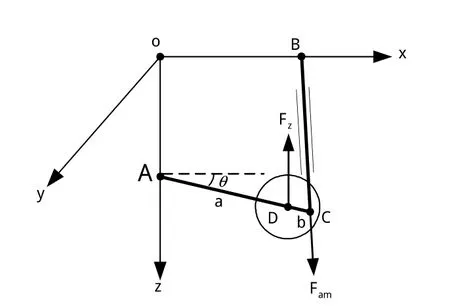
图1 起落架力传递系数分析图Fig.1 Analysis of landing gear force transfer coefficient

对摇臂AC进行受力分析，对A点列力矩平衡方程，则轮轴D上作用的垂向力Fz到缓冲支柱轴向力Fam的传递系数为：

地面平衡计算采用迭代计算的方法，见如图2。

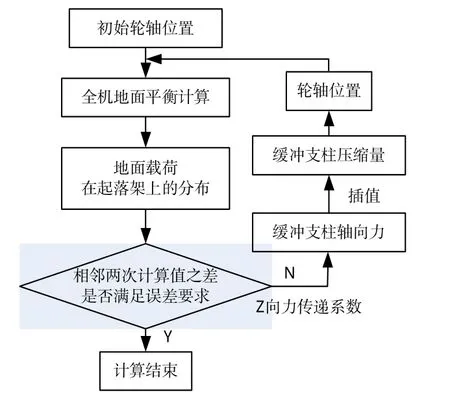
图2 地面平衡计算流程图Fig.2 Process of ground balance calculation

2 跪式起落架等效刚度及等效阻尼计算

跪式起落架由于其结构形式的特殊性，起落架整体的等效刚度和等效阻尼不能通过简单的弹簧阻尼器串并联方式求得。因此，须对跪式起落架的结构特点进行分析，按照一定的等效原则计算跪式起落架整体的等效刚度和等效阻尼。

2.1 等效刚度计算

等效刚度计算时，将起落架视为整体，施加在起落架上某一方向的力与起落架在该力作用下的变形之比即为起落架整体在该方向的等效刚度。

以跪式起落架直升机UH-60主起落架垂向等效刚度计算为例，航向等效刚度的计算同理可求。

UH-60直升机主起落架垂向等效刚度计算模型如图3所示。

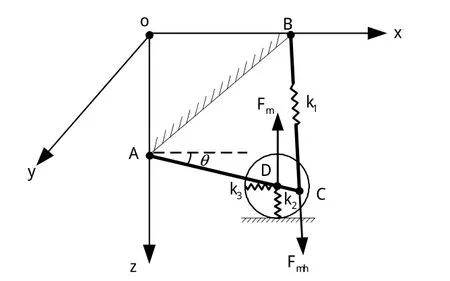
图3 主起落架垂向等效刚度计算模型Fig.3 Calculation model of the vertical equivalent stiffness of the main landing gear

假设起落架整体垂向压缩量δz，即AB杆z向压缩δz，压缩后起落架仍处于平衡状态，平衡后D点较原平衡状态x向和z向分别平移了δdx、δdz，由D点坐标可以求得C点坐标，从而可以得到等效弹簧k1的压缩量，可以得到主起落架垂向刚度等效计算模型：

式（3）中：Fm、Fmh分别表示初始平衡状态下的轮胎支反力和缓冲支柱轴向力；k1、k2、k3分别表示缓冲支柱、轮胎垂向和侧向的刚度系数；A表示初始平衡状态下的点；A′表示AB杆z向压缩δz后的A点，其他各点同理。

解方程组可以得到δdx、δdz，则主起落架垂向等效刚度为：

由于摇臂与机轮轮轴固连，故在不考虑摇臂变形的前提下，摇臂产生多大的侧向位移，轮轴产生同样的侧向位移，故起落架整体的侧向刚度主要表现为机轮的侧向刚度。

2.2 等效阻尼计算

起落架等效阻尼计算时，等效后的系统在某一方向上振动一周所耗散的能量与原系统该方向振动一周所耗散的能量相等。以UH-60直升机主起落架垂向等效阻尼为例，航向等效阻尼的计算同理可得。UH-60直升机主起落架垂向等效阻尼模型见图4。

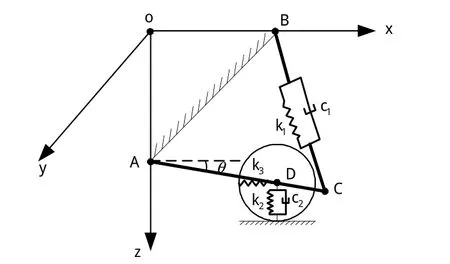
图4 主起落架垂向等效阻尼计算模型Fig.4 Calculation model of the vertical equivalent damping of the main landing gear

在主起落架上施加z=hsin(2πft)的周期垂向振动，则在任意时刻t，A、B两点的垂向位移为hsin(2πft)，A、B两点的垂向运动速度为h⋅2πfcos(2πft) 。

为简化计算，假设AC为轻质杆，则任意时刻AC均处于平衡状态。假设t时刻D点较原平衡状态x向和z向分别平移了δdx、δdz，D点的垂向速度为Vdz，由D点坐标可以求得C点坐标，由D点的垂向速度可以得到C点的垂向速度，进而得到缓冲支柱的轴向压缩（伸长）速度，从而可以得到主起落架垂向等效阻尼模型：

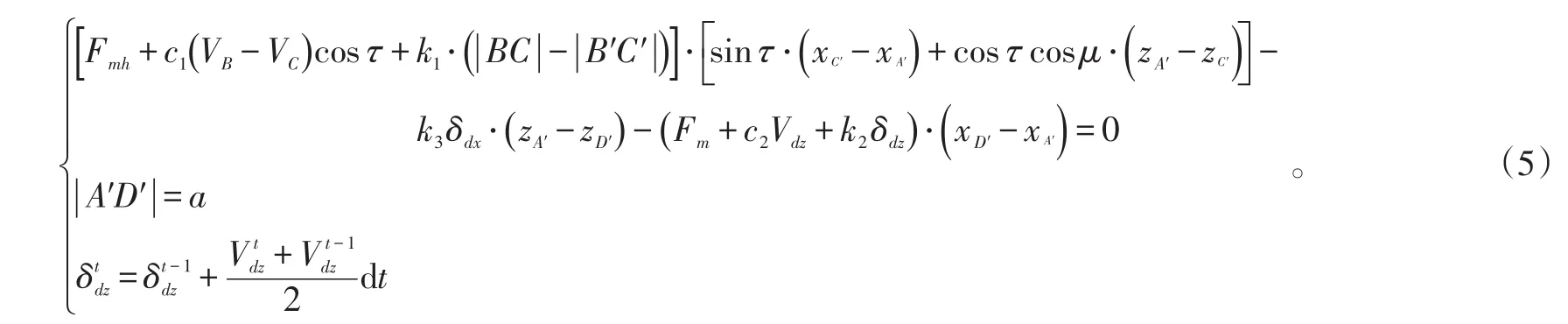
式（5）中，c1、c2分别表示缓冲支柱和轮胎垂向阻尼系数。

解方程组可以得到t时刻的δdx、δdz及VD，则t时刻系统阻尼消耗的功为：

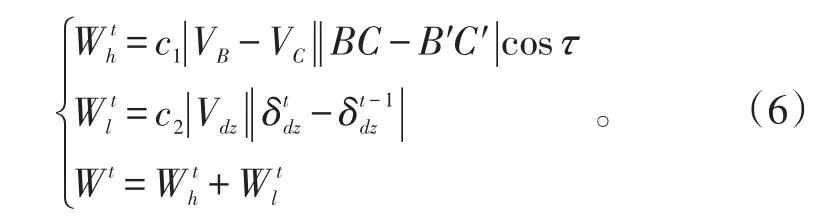
系统振动一周所消耗的功为：

根据等效线性阻尼的计算方法[17]，主起落架垂向等效阻尼可以表示为：

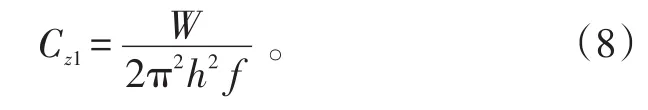
3 起落架参数对滚转模态特性影响分析

采用上述方法计算得到起落架系统的各向等效刚度及阻尼后，按照文献[18]给出的机体运动微分方程计算机体固有模态特性。

以跪式起落架直升机UH-60[19]为例，其机体侧向和纵向各阶模态的固有频率理论计算值与试验值如表1所示，理论误差最大不超过10%，表明上述方法计算得到的跪式起落架系统等效刚度及阻尼能够满足理论计算要求。

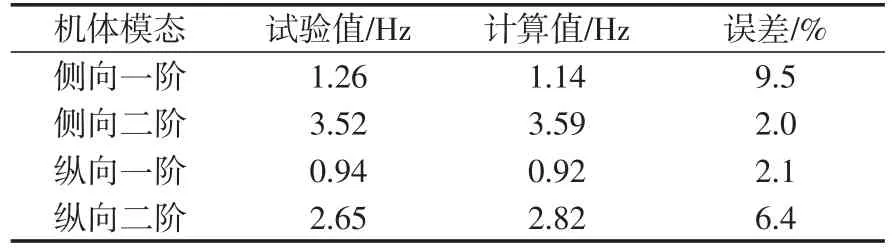
表1 机体各阶模态固有频率Tab.1 Natural frequencies of the airframe

通过改变起落架摇臂与机体纵向对称面夹角（摇臂向外撑开角度）、缓冲支柱与机身连接点位置、缓冲支柱及轮轴长度等跪式起落架结构参数，研究各参数变化对机体滚转模态的影响。

起落架摇臂向外撑开0°、15°、30°时，机体滚转模态频率如图5所示。

图5 摇臂撑开角度对机体滚转模态影响Fig.5 Influence of rocker arm angle on the rolling mode of the airframe

计算结果表明，摇臂向外撑开一定角度，机体滚转模态频率有所提高，撑开30°时，滚转模态频率提高了3.3%。摇臂向外撑开时，主轮距增大，滚转模态频率随之增大。

摇臂撑开 0°、15°、30°，起落架轮轴伸长 0 m 、0.1 m、0.2 m时，机体滚转模态频率如图6所示。

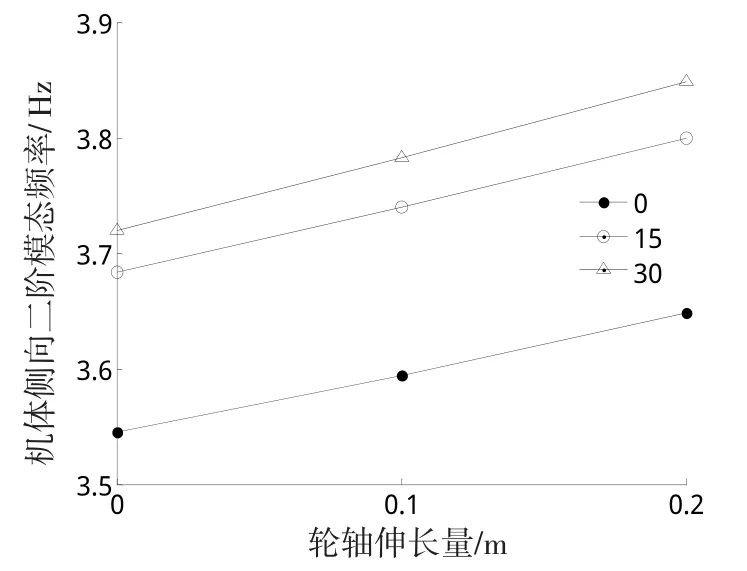
图6 轮轴伸长量对机体滚转模态影响Fig.6 Influence of wheel axle elongation on the rolling mode of the airframe

随着轮轴伸长量的增加机体滚转模态频率增大。其中，摇臂撑开30°，轮轴伸长0.2 m时，机体滚转模态频率最大3.85Hz，提高了6.9%。轮轴长度增大也主要是增加了主轮距，进而引起滚转模态频率的增加。

摇臂撑开 0°、15°、30°，缓冲支柱长度变化-0.2 m、-0.1 m、0 m、0.1 m、0.2 m时，机体滚转模态频率如图7所示。

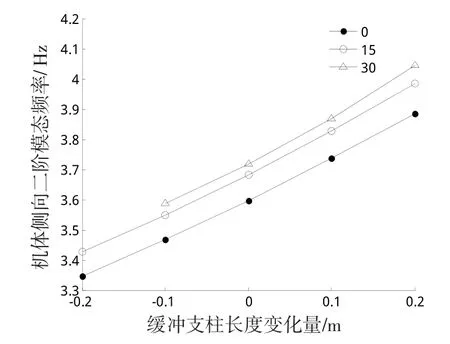
图7 缓冲支柱变化量对机体滚转模态影响Fig.7 Influence of the length change of the oleo strut on the rolling mode of the airframe

缓冲支柱长度增加时，机体滚转模态频率增大。其中，摇臂撑开30°，缓冲支柱伸长0.2 m时，机体滚转模态频率最大4.05Hz，提高了12.4%。

摇臂撑开0°、15°、30°，缓冲支柱与机身连接点z向位移（下移为正）分别为-0.2 m、-0.1 m、0 m、0.1 m、0.2 m时，机体滚转模态频率如图8所示。

图8 缓冲支柱与机身连接点z向位移对机体滚转模态影响Fig.8 Influence of thezdisplacement of connecting point on the rolling mode of the airframe

缓冲支柱与机身连接点z向位移为负，即连接点下移时，机体滚转模态频率增大。其中，摇臂撑开30°，连接点下移0.2 m时，机体滚转模态频率最大4.03Hz，提高了11.9%。

图7摇臂撑开30°，缓冲支柱长度变化-0.2 m和图8缓冲支柱与机身连接点z向上移0.2 m时，计算无法得到机体的侧向二阶模态频率，其主要原因是在这两种情况下，起落架的变化量超出了机体结构限制，使得机轮轮轴上移，机体腹部接触地面，起落架失效，因而计算无法得到结果。

综合分析图7、8的计算结果可知，缓冲支柱长度的增加和缓冲支柱与机身连接点的下移，本质上都是使得机体地面平衡时重心到地面的高度增加，进而引起机体滚转模态频率的增加。

摇臂撑开 0°、15°、30°，缓冲支柱x向位移-0.2 m、-0.1 m、0 m、0.1 m、0.2 m时，机体滚转模态频率如图9所示。

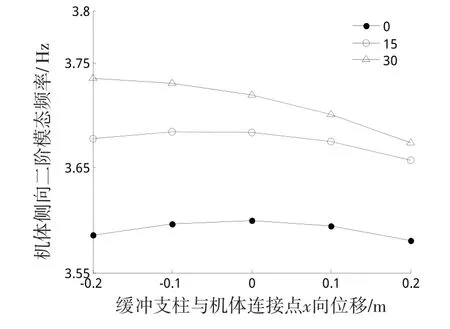
图9 缓冲支柱与机身连接点x向位移对机体滚转模态影响Fig.9 Influence of thexdisplacement of connecting point on the rolling mode of the airframe

缓冲支柱与机体连接点x向平移时，摇臂撑开0°和15°时，机体滚转模态频率略有降低。仅当摇臂撑开30°时，向x轴负方向（机头方向）移动时机体滚转模态频率略有增加且增加幅度很小。因此，缓冲支柱与机体连接点x向平移对机体滚转模态频率的影响不大。

上述分析可知，跪式起落架摇臂外撑一定角度、缓冲支柱及轮轴长度增加、缓冲支柱与机身连接点下移等参数变化能够不同程度的提高机体滚转模态频率。若要最大程度的提高机体滚转模态频率，则需要跪式起落架摇臂外撑角度、缓冲支柱及轮轴长度增加、缓冲支柱与机身连接点下移等因素综合作用。

考虑到直升机机体结构参数限制，缓冲支柱与机身连接点下移量及缓冲支柱伸长量不能无限增加，摇臂外撑角度及轮轴长度也不能无限增大等因素影响，仿真试验中，摇臂外撑30°，缓冲支柱与机身连接点下移0.2 m，轮轴伸长0.2 m时，机体滚转模态频率达到4.35Hz，较起落架参数调整前机体滚转模态频率3.54Hz，提高了22.8%。起落架改进设计前后的机体各阶模态固有频率如表2所示。

表2 改进前后机体各阶模态固有频率Tab.2 Natural frequencies of the airframe before improved and after improved

利用当量二维模型[18]，分别采用起落架改进前后计算得到的机体各阶模态固有特性计算旋翼—机体系统模态频率，起落架改进前后的系统模态频率分别如图10、11所示。

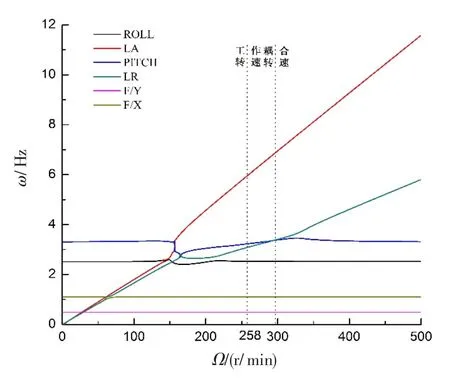
图10 改进前系统模态频率Fig.10 System modal frequency before improvement

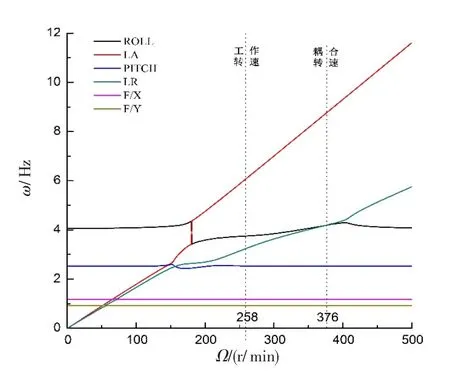
图11 改进后系统模态频率Fig.10 System modal frequency after improvement

由图10可以看出，起落架改进前旋翼的摆振后退型模态与机体滚转模态的耦合转速在300 r/min左右，尽管能够避开258 r/min的旋翼工作转速，但转速裕度在16.3%以下，不能够满足地面共振转速裕度不低于20%的要求，存在地面共振的风险。图10显示，起落架改进后，耦合转速提高到376 r/min附近，此时的转速裕度可达45.7%，能够有效防止地面共振的发生。

另外，从图10、11还可以看出，改进前后，侧向一阶和纵向一阶与旋翼振动模态的耦合转速虽然有变化，但都在100 r/min以内，纵向二阶的耦合转速保持在150 r/min附近，均小于旋翼工作转速，旋翼工作时能够迅速通过，因而几乎不会对地面共振产生影响。

4 结论

1）跪式起落架摇臂外撑一定角度、缓冲支柱及轮轴长度增加、缓冲支柱与机身连接点下移等设计措施能够不同程度的提高机体滚转模态频率。其中，增加缓冲支柱及轮轴长度对提高机体滚转模态频率作用最明显。

2）通过改进跪式起落架结构参数，能使UH-60直升机的滚转模态频率由3.54Hz提高到4.35Hz，提高了22.8%。

3）改进跪式起落架结构参数提高机体滚转模态频率，能够有效改善直升机的地面共振特性且提高滚转模态频率带来的其他模态频率的变化对直升机地面共振的影响不大。