采用丝杠传动的电动舵机运动学分析

徐梦圆，林友志，章心怡

（1.江苏科技大学计算机学院，江苏镇江212000；2.东南大学自动化学院，南京210000；3.江苏科技大学能源与动力学院，江苏镇江212000）

电动舵机是一种典型高精度位置伺服系统，因具有体积小、重量轻、易于控制和可靠性高等特点，大量应用于飞机、导弹、火箭等飞行器[1-3]。在实际的飞行控制系统中，电动舵机是重要的执行机构，其中心任务是执行控制系统发出的指令，即根据飞行控制系统输出的一定大小和极性的信号，驱动舵面按照要求快速、精准地偏转。相较于直线电机作动器，采用丝杠传动的旋转舵机不仅充分利用了旋转电动舵机结构紧凑、效率高的特点[4-5]，而且结合了丝杠灵活性具有减速比大、间隙低、载荷较大等显著优点[6-7]，大大提高了整个系统的控制精度与动态响应，成为高性能的位置伺服作动器的重要组成部分，引起了国内外学者与研究机构的广泛关注[8-9]。

目前，针对旋转电动舵机构成的机电一体化伺服机构的研究主要集中于舵机系统结构设计与控制律设计等方面[10-12]。其中，文献[13]设计了一个导弹舵机控制实验系统，将设计出的控制律即刻加载到导弹舵机控制系统中进行验证，并对设计参数进行调整，以获取最优的控制律，然而文中并没有针对系统结构设计、建模进行详细阐述。文献[14]介绍了一种稀土永磁直流伺服电机和精密微型滚珠螺旋副构成的电动舵机，作者偏重于伺服系统的各组成部分的功能设计。文献[15]主要针对电动舵机存在的易受参数摄动及负载扰动影响、刚度较差的特点，采用鲁棒控制理论，对电动舵机控制系统设计理论及方法进行了深入研究，但仅仅从控制方法入手对系统进行改善。由此可见，虽然传动机构的分析设计在整个控制系统实现中必不可少，尤其是减少传动过程中的非线性因素产生的振荡及精准度下降等问题[16-17]，但针对伺服机构中机械传动环节进行的分析，大多疏于详细介绍机构中非线性建模环节，给实际的工程应用带来了不便。近年来，为实现高保真度伺服系统的研究，细化考虑伺服系统的非线性环节逐渐增多。文献[18]在针对“无刷直流电机/滚珠丝杠副/拨叉”类型电动舵机高保真建模时，介绍了传动机构与负载建模，指出了机构带来的非线性，但缺乏针对机构中的非线性环节进行详细阐述。文献[19-20]在对滚珠丝杠式电动舵机系统非线性特性分析时，主要偏重模型中的间隙与摩擦。本文结合实际伺服系统的作动场景，对传动机构建立了数学模型，分析了电动舵机的旋转运动在经摇臂传动后转为直线运动的过程，确立了传动过程中的正逆运动学关系。对丝杠传动过程中减速比随着舵机转角发生非线性变化进行了推导分析，得到了系统设计参数在运动过程中非线性变化趋势。在机理分析的基础上，并通过模型仿真对推导结果进行了验证，对减少非线性带来的系统振荡，实现系统更精准的控制具有重要意义。

1 结构与工作原理

本文所述电动舵机伺服机构主要由电动机、齿轮减速机构、丝杠传动机构、输出机构及反馈信号装置5个部分构成。其中，电动机为舵机系统提供原动力；减速机构主要由减速齿轮构成，通过减速比的调整来完成电动机输出转速与驱动舵面输出转速的匹配；丝杠传动机构通过改变力的方向，以实现其曲线圆周运动到直线运动的转变；输出机构是由连杆和摇臂构成，通过连杆运动带动摇臂输出一定的偏转角，进而作用于系统输出舵面。

如图1所示，在整个伺服系统机构简图中，当电动机接收控制器输出的给定信号开始转动，而后经过两级减速器，再由丝杠将圆周运动转化为直线运行，在此过程中，系统的运动信号传递始终是线性的。因连杆连接的摇臂在受往复惯性力的作用下，来回地周期性摆动，从而导致输入信号与输出信号的线性关系发生变化，在系统中引入了非线性环节，这也给复杂的实际系统分析增加了难度，甚至会导致系统内部发生振荡等问题。因此，为了补偿非线性环节，改善可能的系统振荡，提高系统的输出精度，基于该结构的模型建立与运动学分析尤为重要。

图1 丝杠传动的电动伺服系统简图Fig.1 Structure diagram of electric servo system driving by screw

2 数学模型

2.1 模型假设

考虑到虽然齿轮传动间隙和零件弹性变形的因素不可避免，但对系统影响极小。为了便于模型的抽象和分析，引入如下基本假设：①忽略齿轮传动间隙；②忽略零件的弹性变形。

2.2 模型建立

如前所述，输出的非线性主要来源于输出机构的连杆与摇臂，根据系统中输出摇臂与连杆的连接情况，抽象为图2模型。图中以摇臂的固定输出点为坐标原点，以摇臂和连杆垂直时摇臂所在位置的竖直向下方向为x轴正方向，以水平向右的方向为y轴正方向，从而复原了摇臂与连杆的空间关系。当摇臂向左摆动时所产生的回转角θ为负，向右摆动θ为正。图2中，R为摇臂的回转半径/mm；l为连杆的长度/mm；Δl为丝杠螺母运动位移量/mm；θ为摇臂往复运动的回转角，且θ大小在实际的摇臂回转范围内。

图2 传动机构的抽象模型图Fig.2 Abstract physical model of transmission section

3 逆运动学分析

3.1 位置逆运动学

在图2坐标轴的基础上，若伺服系统的实际输出为期望输出，即摇臂输出的回转角θ已知，那么根据图2中的位置几何关系，利用勾股定理可求解出丝杠螺母运动位移量为：

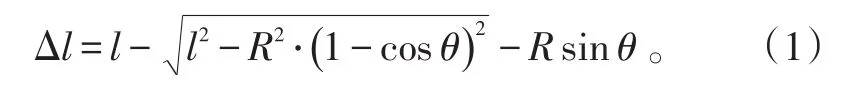
又因为丝杠移动位移量与电机输出转角需经过齿轮减速，则有电机机械角度α与丝杠移动位移量Δl的关系为：

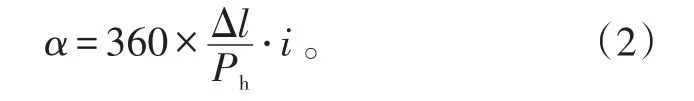
式（2）中：i为舵机中齿轮传动机构减速比；Ph为丝杠的导程/mm。

3.2 速度逆运动学

由位移与速度的物理关系，对式（2）求导，可得速度的逆运动学方程为：

电机转速为：

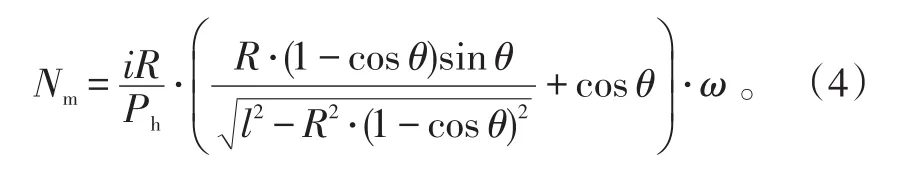
4 正运动学分析

4.1 位置正运动学

从电动机运动到摇臂输出时，若给定电机转速一定，旋转运动到直线运动的丝杠螺母运动位移量为Δl，对式（1）化简后，两边取平方，求解得摇臂输出回转角与电机经丝杠输出位移量的正运动学关系为：

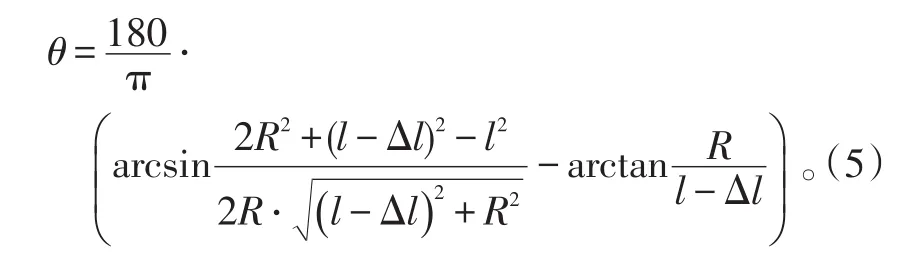
4.2 速度正运动学

摇臂的回转角速度为：

摇臂的回转输出转速为：

5 仿真及结果分析

在Matlab中搭建丝杠传动的电动舵机的运动学模型，对伺服系统的传动机构进行了数值仿真，仿真分析用来研究丝杠传动的电动伺服系统中传动机构产生的非线性影响以及验证机理分析的可靠性。仿真采用的舵机系统模型参数与实际伺服系统一致，具体如下：摇臂长度R=65mm，连杆长l=80mm，丝杠导程Ph=20mm，电动机额定转速NR=1 600rpm，摇臂输出回转角最大范围为(-30°,30°)。

若传动机构中采用普通齿轮减速，且减速比i=2.8，当输出摇臂回转角在期望输出范围内时，此时传动丝杠的位移变化量Δl。如图3中实线所示，可知因受非线性因素的影响，丝杠随摇臂回转角的变化与理想的线性拟合存在带状的偏差，与上节分析一致，式（3）中由于传动机构中三角函数的引入给系统模型带来了非线性。

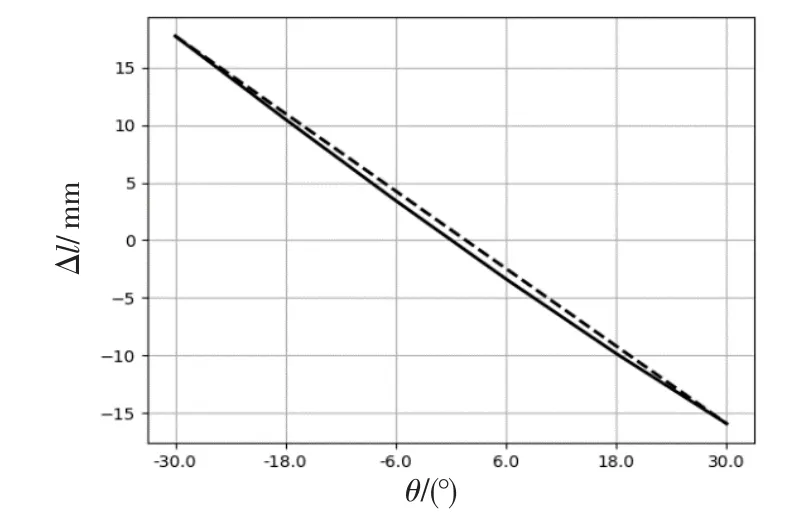
图3 丝杠位移随摇臂转角变化关系Fig.3 Displacement of screw vs rocker arm angle

图4与图5分别表明了非线性环节对电机端输出机械角与转速产生的影响。其中，为保证输出回转角满足要求，图4中机械角发生了不规整的周期变化及幅值差异。而从图5中可以看出，实际输出的电机转速在额定转速附近变化。然而，在实际精密的伺服系统中，作为动力驱动，电机在接受控制器指令后，会准确地发生旋转。因此，为了补偿装置中的非线性环节，利用上节的运动学分析设计相关参数。若采用行星齿轮、谐波减速转置或螺母可调节的多齿轮结果的减速装置，在电动机额定转速下，可通过调节传动机构中的减速比来减小系统的非线性影响，实现系统摇臂输出角度在期望值的容差范围内。针对本文的舵机系统，图6给出了减速比随摇臂回转角的变化趋势。

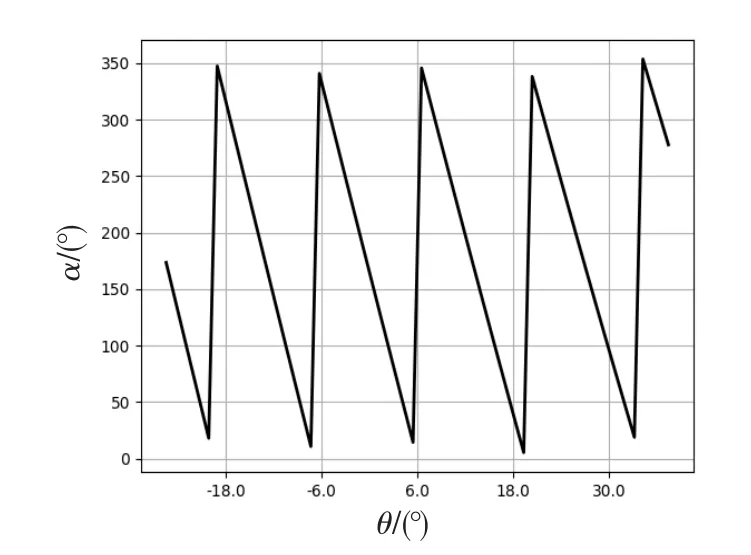
图4 舵机周期运动机械角与摇臂转角关系Fig.4 Periodic motion of electric actuator vs rocker arm angle

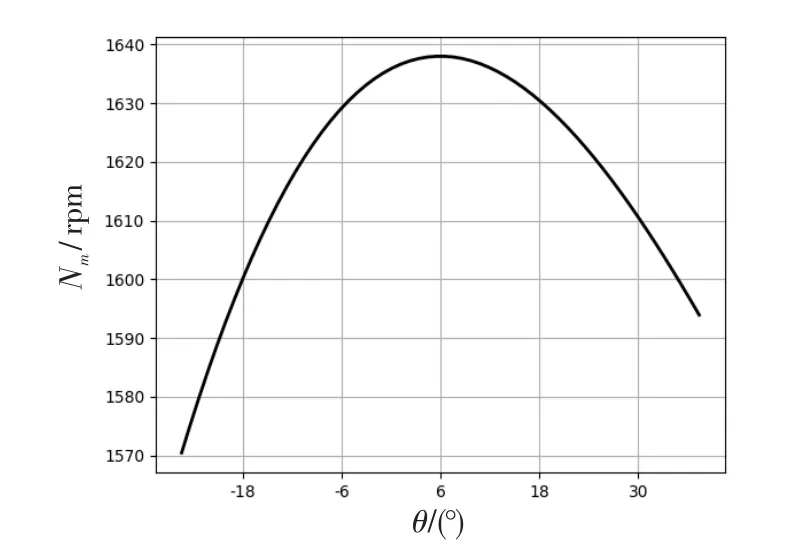
图5 舵机输出转速与摇臂转角关系Fig.5 Output speed of electric actuator vs rocker arm angle

图6 减速比参数设计与摇臂转角关系Fig.6 Parameter design of reduction ratio vs rocker arm angle

6 结论

本文通过对丝杠传动的电动舵机伺服系统进行建模分析，对其中传动机构的非线性环节，从位置、速度两个方面进行了正逆运动学解算，利用推导的运动学方程对伺服系统中的传动过程进行了分析，并在系统的数值仿真中，验证了模型分析的正确性。在此基础上，提出了一种通过传动机构参数设计的方法补偿伺服系统中的非线性环节，该方法从理论上能够准确地补偿系统中的非线性影响，而且思路明确、简单易行，为提高系统的控制精度与降低系统跟踪误差提供了参考，具有一定的理论和工程价值。