基于部分模糊度解算的BDS/GPS组合RTK算法

刘 伟，李长庚，满小三

(1.中南大学 物理与电子学院，湖南 长沙 410012;2.湖南格纳微信息科技有限公司，湖南 长沙 410005)

在GNSS精密RTK定位中，利用载波相位实现快速高精度定位的关键在于快速可靠地解算整周模糊度。由于多星座多频率组合RTK定位逐步进入实际应用，模糊度维数显著增多，搜索空间增大，导致全模糊度固定失败。因此，可以利用部分模糊度固定算法，降低模糊度维数，提高模糊度的固定率及定位可靠性。Teunissen最早提出了部分模糊度固定的概念，并基于电离层加权无几何GPS模型分析部分模糊度固定的成功率，而没有应用于几何GNSS定位模型[1]。Cao W等分析了GPS和Galileo及其组合情况下的模糊度固定成功率，并以此提出多星座多频率组合部分模糊度固定算法[2]。Wang等分析了多GNSS星座条件下部分模糊度固定的可靠性，并给出了一种部分模糊度固定算法[3]。李金龙针对多频组合情况下，提出一种多频快速部分模糊度解算策略[4]。

当进行GNSS定位解算时，新升起的卫星，高度角比较低。而低高度角卫星的观测值观测噪声大，受多路径及大气延迟误差的影响更为严重，致使其模糊度难以固定[5]。同时，在某些情况下，由于相位观测值的粗差异值、双差之后大气延迟误差未完全消除及多路径等误差影响，也会导致模糊度固定失败[6-8]，模糊度固定成功率是一个理论上非常严密的评价尺度。通过它求出的模糊度固定解在多大程度上接近模糊度真值。当模糊度固定成功率足够大时，才认为其解是可靠的[9]。

因此，适当缩减模糊度的个数，剔除一些有问题的观测值，只固定模糊度中的一部分可以提高模糊度解算的成功率，同时也会提高模糊度固定的效率。本文提出的部分模糊度方法通过综合考虑卫星高度角、模糊度固定成功率及Ratio值来筛选卫星进行模糊度解算。通过算例分析表明：该方法可以有效地提高BDS/GPS组合RTK的模糊度固定率及定位的可靠性。

1 BDS/GPS RTK数学模型

BDS/GPS组合RTK的双差函数模型矩阵形式为

Dbp=DAdX+εp.

(1)

Dbφ=DAdX+DλN+εφ.

(2)

式中：A为设计矩阵，dX表为流动站u三维位置的改正数；Ni表示为站间单差模糊度参数；εP,εφ分别为双差码观测噪声和载波相位观测噪声，D为站间单差转双差的转换矩阵。

BDS/GPS组合RTK定位的双差函数模型的未知参数向量形式：

.

(3)

通过Kalman滤波解算方程，获取未知参数向量Y及其协方差矩阵QY。其中Kalman 滤波未知参数向量Y的初始值，位置参数的初始值可以使用单点定位解获取，站间单差模糊度初始值可以由站间单差伪距与站间单差相位做差来获取。

由于未知参数Y包含的站间单差模糊度Ni为实数，不具有整周性。获得由实数参数dX和双差整周模糊度▽Ni参数组成的新的未知参数向量Y′及其协方差矩阵QY′。

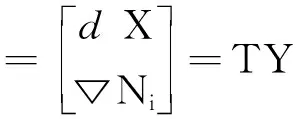
(4)

(5)

式中：E为单位矩阵，QdX为实数参数dX协方差矩阵，Q▽Ni为双差整周模糊度参数▽Ni的协方差矩阵，Qd X▽Ni为实数参数dX和双差整周模糊度参数▽Ni的互协方差矩阵。

在获取未知参数向量Y′及其协方差矩阵QY′后，再通过应用LAMBDA方法即可固定双差整周模糊度，从而获得实数参数dX的固定解。

2 部分模糊度固定策略

.

(6)

(7)

部分模糊度解算目的在于获取最大成功率的模糊度固定解，提高参数的估计精度，不同模糊度子集会带来不同的解算效果。因此，部分模糊度解算关键在于如何选取最优的模糊度子集。通过综合考虑卫星高度角、模糊度固定成功率及Ratio值来筛选模糊度子集(见图1)。具体步骤如下：

ei

2)设置模糊度固定成功率阈值PT，若PS>PT；直接进入第四步；

4)若第三步中的形成新模糊度个数大于3个，使用LAMBDA算法进行模糊度解算，反之，直接进行第六步；

5)计算ratio值，若ratio>k(阈值)则获取参数的固定解，解算结束，反之进入下一步；

6)获取参数的浮点解，解算结束。

3 算例分析

本文采用GPS/BDS二系统四频测量型接收机于2015-09-18在郑州市收集一组16.4 km的动态数据，流动站位于跑车的顶部，跑车的轨迹见图2。数据采样间隔为1 s，收集时长约1 h。在实验中，设定截止高度角为20°，模糊度固定成功率的阈值为99%，ratio值的阈值为2，采用单历元固定模糊度。评估部分模糊度解算(PAR)的性能，采用模糊度固定率及定位误差(与商业软件GrafNav解算的GPS+BDS双频RTK固定解的差值)作为评估指标，与全部模糊度解算(FAR)进行对比分析。

图1 部分模糊度解算的流程

图2 动态测试的跑车轨迹(左图：完整轨迹，右图：局部轨迹)

从图3可知，在整个动态测试期间，由于遮挡卫星存在频繁的失锁，致使个别卫星的模糊度固定失败，从而导致全部模糊度固定失败。因此，可以采用部分模糊度固定技术固定模糊度。

从图4可以看出，两种模糊度解算方法在2050历元、2505历元及2580历元处，模糊度固定成功率都下降至30%以下，其主要原因是该历元可见卫星数低于6颗，导致其卫星—测站空间几何结构差，从而使其ADOP值变得比较大。而在其他时段，采用部分模糊度固定技术的模糊度固定成功率(ADOP)基本保持在100%，而采用全模糊度固定会导致模糊度固定成功率降低(开始时刻及3 800～3 900历元期间)。由此可见，PAR方法优于FAR。

从图5—图6可以看出，采用部分模糊度固定技术通过Ratio值检验(红线以上)的历元明显比全模糊度固定解算多，通过统计可知模糊度固定率从79.9%(FAR)提高到99.1%(PAR)。即采用部分模糊度固定解算对BDS/GPS组合RTK的模糊度固定率提高了20%，从而导致其RTK定位解的精度更高。

图3 动态测试期间流动站的可见卫星数(GPS+BDS)

图4 单历元模糊度固定成功率

图5 单历元模糊度解算的Ratio值序列(FAR)

图6 单历元模糊度解算的Ratio值序列(PAR)

图7 BDS/GPS组合双频RTK的定位固定解误差序列(FAR)

图8 BDS/GPS组合双频RTK的定位固定解误差序列(PAR)

如图7—图8所示(剔除模糊度固定错误的历元)，在0～500历元处，BDS/GPS组合双频RTK采用PAR可以获取固定解，而采用FAR不能得到固定解。而在其他时段，结合图5和图6可知，FAR方法存在大量的模糊度固定失败情况(Ratiok)。由此可见，本文提出的PAR技术是有效的，可以提高BDS/GPS组合双频RTK模糊度固定率及定位的可靠性。结合表1可以看出，采用PAR方法的BDS/GPS组合RTK定位精度优于FAR方法，相比于全模糊度解算(FAR)，部分模糊度解算(PAR)对BDS/GPS/GLONASS组合RTK定位精度改善不大但定位的可靠性更高。

表1 采用两种模糊度解算方法获得BDS/GPS/GLONASS组合RTK固定解的定位精度 m

4 结 论

本文通过综合考虑卫星高度角、模糊度固定成功率及Ratio值提出部分模糊度固定算法，该算法可以有效地剔除有问题的卫星，筛选出最优的卫星组后定位RTK。通过算例分析：相比于全模糊度解算(FAR)，部分模糊度解算(PAR)可以有效地提高BDS/GPS组合RTK的模糊度固定率及定位的可靠性，其模糊度固定率从79.9%(FAR)提高到99.1%(PAR)，虽然定位精度改善不大，但定位的可靠性明显改善。