陕西省GPS基准站垂直形变的陆地水负荷效应

郑增记, 苏利娜, 范丽红,翟宏光, 张永奇, 韩美涛

(1.陕西省地震局，陕西 西安 710068; 2.中国科学院上海天文台，上海 200030;3.长安大学 地质工程与测绘学院，陕西 西安 710054)

随着GPS技术的快速发展，无论其水平形变还是垂直形变均已广泛用于研究地壳运动和板块运动。地壳的垂直形变通常包含构造形变和非构造形变两类信息，其中非构造形变主要是由大气、海洋以及陆地水变化等造成的季节性垂直性变，尤其是陆地水导致的垂直形变在某些地方可达30 mm[1]。通过对GPS观测进行非构造形变的改正可以更好地研究地壳的构造运动，目前对非构造形变的改正主要通过地球物理模型数据[2-4]。2002-3-17 GRACE卫星发射后，基于GRACE研究陆地水迁徙所造成的垂直形变也得到了大量应用[5-8]。

陕西省位于我国大陆东西和南北巨型构造单元的交接地带，既是华南地块向华北地块的过渡带，也是青藏地块与华北地块的过渡带，是华南地块、华北地块和青藏地块的连接枢纽，历史上曾发生过华县8级大地震，具有发生强震的构造背景[9]。本文利用2012-01—2015-12陕西省连续GPS基准站数据以及同期的GRACE、GLDAS数据定性比较和分析由陆地水导致的季节性垂直变化，为获取研究地震有用的构造形变信息提供依据。

1 数学模型

1.1 GPS估计形变

GPS跟踪站的坐标时间序列通常用常数项、线性趋势项、周年和半年项以及噪声项来表示，即

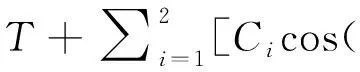
(1)

式中:A为常数项，B为线性趋势项，ωi为振幅Ci和Di的周期项角频率，Δt为相对参考历元的时间差，i=1、i=2分别代表周年项、半周年项，ε为噪声项。

1.2 GRACE估计形变

采用GRACE时变重力资料解算地表垂直负荷形变

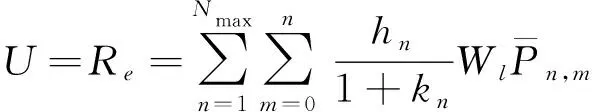
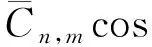
(2)

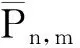
1.3 GLDAS估计形变

根据Farrell[10]的负荷理论计算地表流体负荷垂直位移

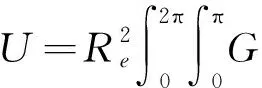
(3)

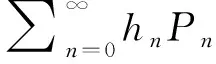
(4)

式中:ψ为计算点到负荷源的角距；G(ψ)为负荷格林函数；H(ψ，A,t)是负荷质量层在t时刻的厚度；A是从计算点到负荷源的方位角；通过GLDAS模型提供的H可以计算任意一点的垂直位移。

2 数据处理与结果分析2.1数据介绍2.1.1 GPS数据

本文首先解算陕西省22个GPS基准站(如图1所示)2012-01—2015-12共48个月的观测数据。利用GAMIT解算22个基准站和周围13个IGS参考站获得单日松弛解，解算中采用LC观测值消除电离层一阶项，采用GMF/GPT模型改正对流层延迟，每2 h估算一个对流层延迟参数。此外，在解算过程中施加固体潮、海潮和极潮改正，但未进行大气潮和非潮汐海潮改正。然后，利用GLOBK将单日松弛解与全球参考框架H文件联合平差，选择80个IGS核心站进行约束，计算测站在ITRF2008参考框架下的坐标时间序列。

图1 陕西省GPS基准站分布

2.1.2 GRACE数据

采用美国德克萨斯大学空间研究中心(UTCSR)最新发布的RL05月重力场模型数据，时间跨度为2012-01—2015-12(实际有效数据为37个月)。UTCSR RL05模型数据为处理后的规格化重力场位系数，最大阶数为60阶，该模型已扣除极潮、固体潮、海潮的影响以及大气、海洋的非潮汐部分影响，并且相较于RL04模型，RL05模型在信噪比方面有显著提高。

GRACE对C20项不敏感，其精度较低，在计算时采用SLR的C20值进行替换[11]。由于GRACE本身无法确定地球重力场的一阶变化，其一阶位系数为0，为了保持与GPS参考框架的一致性，本文采用Swenson等估算的一阶重力位系数[12]。GRACE卫星重力场的高阶球谐系数解主要受噪声影响，并且重力场球谐系数的奇偶阶存在相关性，本文采用300 km高斯滤波平滑以及P3M6方法进行去相关处理[13]。

2.1.3 GLDAS数据

采用全球陆地数据同化系统(Global Land Data Assimilation System,GLDAS)Noah水文模型计算地表垂直负荷位移。GLDAS Noah水文模型的空间分辨率为0.25°×0.25°，时间分辨率是3 h，将Noah模型包含的地表4层土壤水(0～200 cm)、雪水当量以及冠层蓄水数据综合得到总的水储量数据，并扣除2012-01—2015-12的均值得到水储量变化值，从而通过式(3)计算地表垂直负荷位移。

2.2 结果分析

图2为部分GPS站点GPS、GRACE以及GLDAS垂直形变时间序列，从图2可以看出，垂直形变具有明显的周期性特征，从均方根(RMS)、相关性、周年振幅与初相位4个方面对GPS、GRACE以及GLDAS垂直形变时间序列进行定量分析和比较。

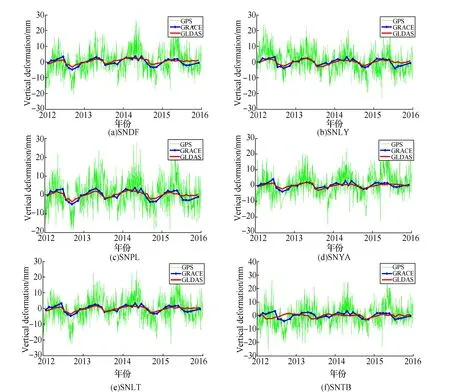
图2 部分连续GPS站垂直形变时间序列

2.2.1 RMS与相关性比较

为了便于GPS、GLDAS与GRACE相比较，按照月时间分辨率对GPS和GLDAS分别进行了平滑。首先分析了扣除GRACE、GLDAS前后GPS高程RMS减少的百分比，

RMS(%)=

RMS(GPS)-RMS(GPS-GRACE/GLDAS)RMS(GPS).

(5)

其次，利用皮尔森相关系数分别计算GRACE、GLDAS与GPS垂直时间序列的相关性，计算式：

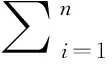
(6)

表1给出各站GPS时间序列分别扣除GRACE、GLDAS负荷形变后RMS减少量以及GPS与GRACE、GLDAS时间序列的相关系数结果。

由表1可以得出：

1)除SNTB站点外，其余GPS站点时间序列扣除GRACE或GLDAS后，其RMS值均减少，两者的RMS减少平均值分别为11.7%、11.0%，即GPS垂向时间序列中，11.7%来源于GRACE水负荷形变，11.0%来源于GLDAS水负荷形变；

2)由于SNTB站点的GPS垂向时间序列与GLDAS垂向时间序列的相关系数为0，所以扣除GLDAS后，GPS垂向时间序列RMS值并没有减少反而增加了；

3)63%的GPS站点与GRACE的相关系数大于等于0.5，77%的GPS站点与GLDAS的相关系数大于等于0.5；GPS与GRACE、GLDAS的相关系数的平均值分别为0.48和0.51。

2.2.2 周年振幅与初相位比较

表2为GPS、GRACE以及GLDAS模型所计算的垂直位移周年信号的振幅与初相位。

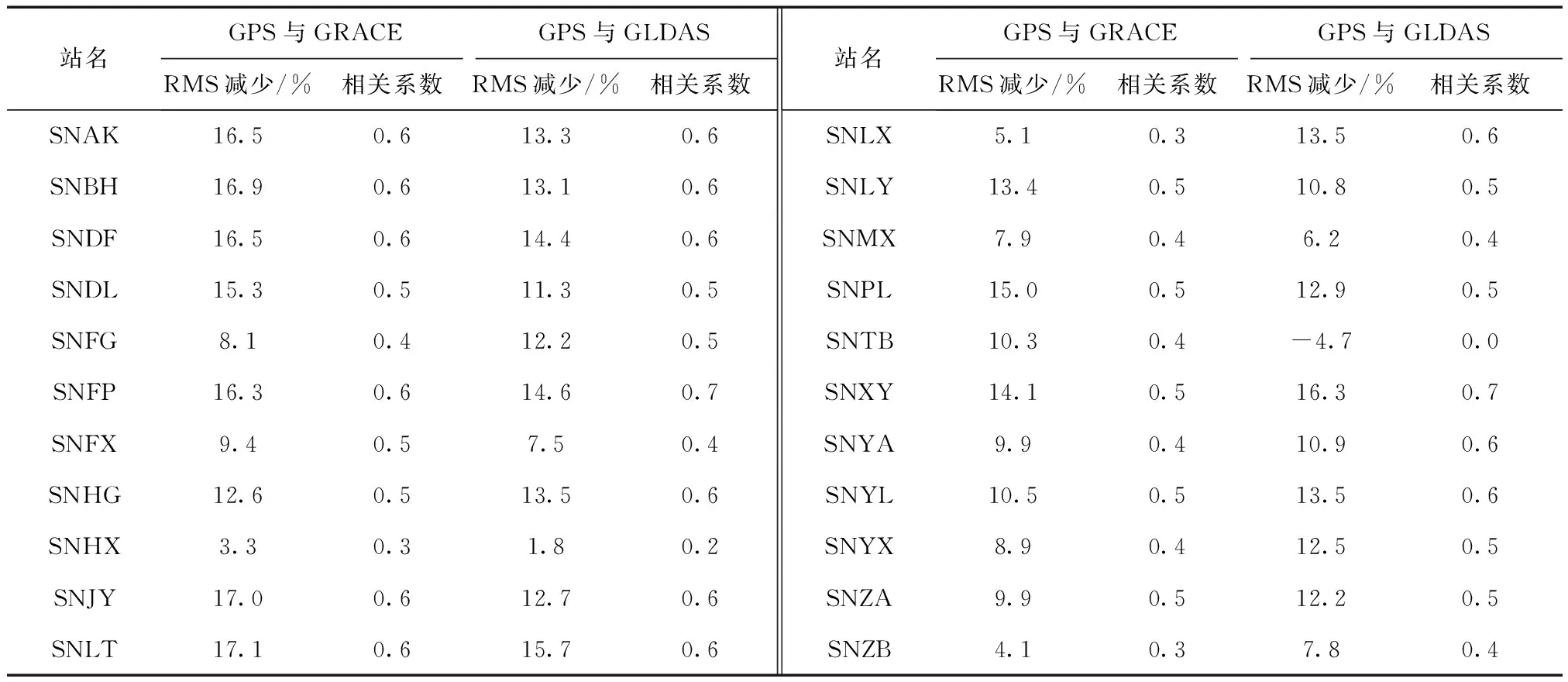
表1 各站GPS与GRACE及GPS与GLDAS RMS减少量和相关系数

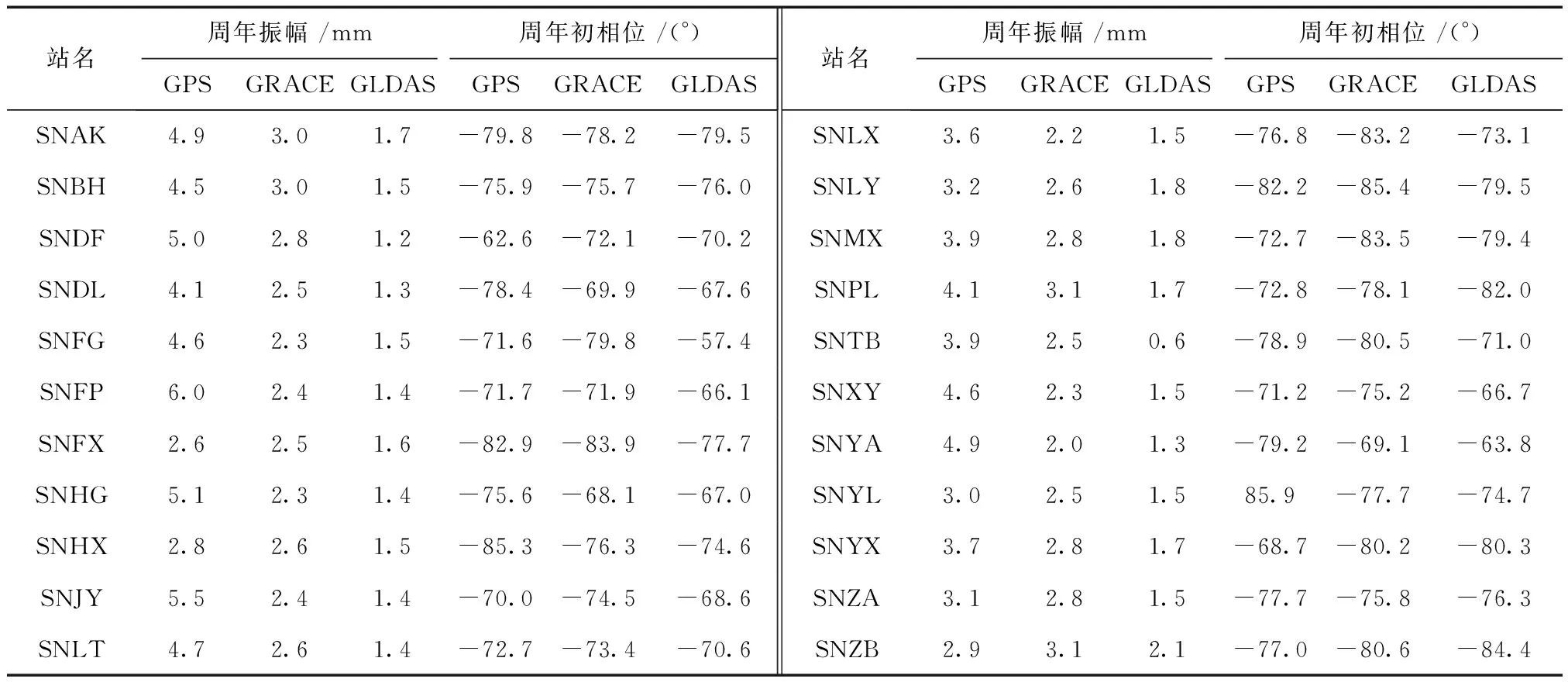
表2 GPS,GRACE及GLDAS模型所计算的垂直位移周年信号的振幅与初相位

由表2可以看出：

1)对于振幅而言，大部分台站GPS与GRACE的振幅较为接近，而GLDAS模型的振幅与它们二者的差异较大；对于初相位而言，三者计算结果符合的较好，这也同时验证了GRACE与GLDAS模型的准确性；GRACE与GPS的初相位之差，有86%站点位于-10°～10°之间，GLDAS与GPS的初相位之差，有68%站点位于-10°～10°之间。

2)GPS的振幅约为2.5～6.0 mm，站间差异较大；另外，由于GPS观测的垂直形变具有全波段信号，因此GPS站点(除SNZB外)的振幅均大于GRACE和GLDAS；SNZB站的GPS振幅比GRACE偏小，主要因素可能与该点本身观测资料或数据处理有关，具体原因有待进一步研究。

3)由于GRACE空间分辨率较低，所有站点的振幅基本一致，大致在2.0～3.0 mm；GLDAS的振幅最小，大致在0.5～2.0 mm；GLDAS的振幅较GRACE小，主要是由于GLDAS模型不包含地下水数据。

3 结束语

本文通过对陕西地区2012-01—2015-12 GPS,GRACE以及GLDAS陆地水负荷形变时间序列分析与比较后发现：

1)陕西省GPS基准站的垂向形变时间序列中，陆地水负荷形变并不显著，只有大约11.7%来源于GRACE垂直负荷形变，大约11.0%来源于GLDAS垂直负荷形变；

2)GPS与GRACE以及GPS与GLDAS的相关系数大于等于0.5的站点比例分别是63%和77%；

3)对于振幅而言，GPS的振幅最大，GRACE的振幅其次，GLDAS的振幅最小；对于初相位而言，三者计算结果符合的较好。

扣除GRACE后，GPS时间序列的RMS并未明显减小，一部分原因是GPS数据处理中引入的误差，例如,基岩的热胀冷缩、轨道误差以及大气潮、非潮汐海潮等模型误差，另一部分原因是GRACE数据处理过程中的截断误差以及高斯滤波平滑的影响，相信新一代重力卫星GRACE-Follow on发射后，GRACE数据误差的影响将大大减小。