基于抗差岭估计的相机标定方法

王俊威，西 勤，冯其强，郭迎刚，王永强

(1.信息工程大学，河南 郑州 450001; 2.中测国检(北京)测绘仪器检测中心，北京 100039)

近年来，随着数码成像技术的快速发展，数码相机得到广泛应用，很多数字工业摄影测量系统都以普通数码相机作为影像传感器来获取数据。数码相机虽然具有体积小、重量轻、使用方便等优点，但也存在畸变差较大、内方位元素不稳定等缺陷，因此，数码相机在被应用于摄影测量前需要先对其进行标定[1]。

相机标定的目的是为了恢复每张像片光束的正确形状，以保证像点、投影中心和对应的物方点在同一条直线上。标定的实质就是确定拍摄像片时相机的外方位元素和内方位元素。十参数畸变模型能较好地补偿各种可预见的畸变差，是目前数字工业摄影测量中应用最广泛的相机畸变模型[2]。但相机畸变模型中各畸变参数之间、畸变参数与摄站参数之间存在近似的线性关系，即过度参数化现象[3]。

针对相机参数间相关性问题，于英提出基于岭估计的相机标定方法[4]，提高相机参数求解精度。但此方法没有抵抗粗差的效果，而摄影测量中粗差与偶然误差、系统误差是同时存在的[5]，粗差产生的原因主要有同名像点匹配出错、超过随机范围的偶然误差等。抗差等价权能通过逐次迭代平差结果来平衡观测值之间的比重[6]，使含粗差的观测值的权减小或降为零，进而减弱粗差的影响或剔除粗差。结合抗差估计和岭估计，本文提出基于抗差岭估计的相机标定方法，不仅可以有效地解决标定模型结构中的参数相关性问题，而且可以有效地抵制观测粗差的影响，进一步提高相机标定结果。

1 相机标定模型

1.1 十参数畸变模型

相机标定的重点内容是内方位元素和畸变参数。内方位元素是确定相机镜头中心相对于影像位置关系的参数，包括像主点相对于像片几何位置(x0,y0)和相机主距f。畸变参数包括：径向畸变、偏心畸变和像平面畸变。

十参数畸变模型表示为

.

(1)

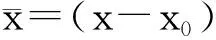
1.2 相机标定模型

利用十参数模型作为附加参数，则含畸变改正值的共线条件方程为

.

(2)

式中:(ai,bi,ci)(i=1,2,3)为由外方位角元素组成的旋转矩阵各元素;(X,Y,Z)为物方点坐标;(XS,YS,ZS)为外方位元素的线元素。

线性化后的误差方程可写为

V=A1X1+A2X2+A3X3-L,P.

(3)

式中:X1,X2,X3分别为物方点坐标、摄站参数和相机参数改正值;A1,A2,A3分别为误差方程的系数;L为常数向量;P为单位权矩阵。

2 抗差岭估计

2.1 抗差岭估计的基本原理

抗差岭估计是抗差估计和岭估计的组合[7]。抗差估计(又称稳健估计)的基本思想是将最小二乘估计的权以等价权代替，使所估计的未知参数尽可能减免粗差的影响或抗拒异常值的干扰，从而获得可靠有效的参数估值。岭估计则是在最小二乘估计法方程系数阵的对角线上增加一个合适的正数，生成新的法方程系数阵，通过改善原来系数阵的相关程度来提高所求结果的精度和稳定性[8]。

将误差方程(3)改写成

,P.

(4)

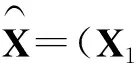
根据抗差岭估计原理，参数的抗差岭估计解为

.

(5)

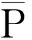
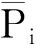
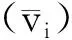
(6)

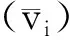
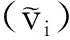
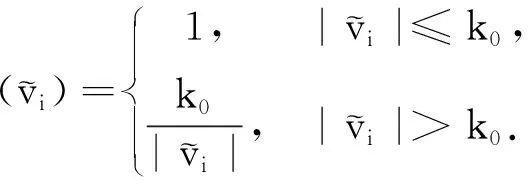
(7)

式中：k0为保权临界值，此处取k0=2[9]。

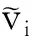
，i=0,1,…,n-1.

(8)

式中:vi为观测值残差；mvi为vi的中误差。

mvi由式(9)计算为

.

(9)

式中：σ0为单位权中误差；Ai为矩阵A的第i行，即第i个误差方程的系数向量。

.

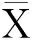
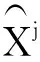
(10)

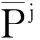
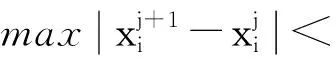
2.2 法方程病态的判断

法方程是否病态一般根据其系数阵的条件数来判断，法方程系数阵的条件数按式(11)计算,为

.

(11)

式中：N为法方程系数阵；λmax,λmin分别为N的最大、最小特征值。

一般认为当condN<100时，法方程病态程度很小；当100≤condN≤1 000时，法方程中等程度病态；当condN>1 000时，法方程严重病态[4]。

2.3 岭参数的选择

引进岭估计的目的是减小均方根误差，而岭参数k的确定方法有很多，常用的方法主要有岭迹法和双h公式法[11]。由于岭迹法缺乏严格的理论依据，k值的确定具有主观随意性，本文选择双h公式法确定k值。其算式为

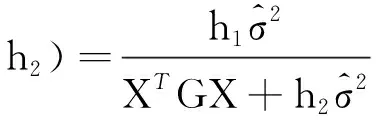
(12)

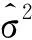
若取G=I，h1=t，h2=0，则式(13)变为

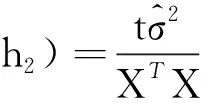
(13)

式中，t为未知参数的个数。

3 基于抗差岭估计相机标定的流程

抗差岭估计需要待求未知参数的初始值来进行迭代求解，内方位元素的初始值除焦距f取21 mm外，其余都取为零。用MetronIn-DPM[12]软件处理像片来获得外方位元素的初值。在获得内、外方位元素的初始值后，计算法方程系数阵并判断其是否为病态。如果是病态，则采用抗差岭估计的方法；如果不是病态，则采用抗差估计的方法。相机标定流程如图1所示。

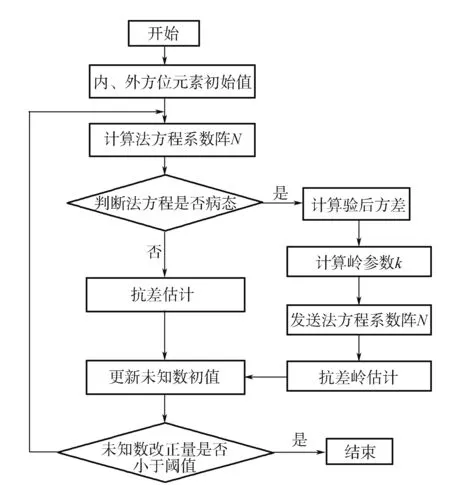
图1 抗差岭估计相机标定流程

图2 实验器材

4 实验及分析

4.1 相机标定对比实验

在尺寸为80 cm×70 cm的矩形木板平面上均匀布设30个直径为6 mm的摄影测量回光反射标志和9个编码标志，以此作为实验标定板，如图2所示。用Nikon D810相机在距离标定板约2 m处的不同位置对标定板拍摄3张照片。再用美国GSI公司的量测型INCA3相机对标定板拍摄， VSTARS摄影测量系统进行处理。由于V-STARS系统配合INCA3的测量精度可达5 um+5 um/m[13]，即2 m范围内的测量精度达到0.015 mm，因此可以将V-STARS处理得到的标志点坐标作为真值。均匀选择15个标志点作为控制点，利用抗差岭估计法对Nikon D810相机进行标定解算，剩余15个点用作检验。实验中，计算的首次迭代时法方程系数阵的条件数远远超过1 000，故属于严重病态。

分别采用最小二乘估计平差(LS)、岭估计平差(RE)和抗差岭估计平差(RR)计算Nikon D810相机的内外方位元素。所得外方位元素结果如表1所示，内方位元素结果如表2所示(经计算3种方法求得各参数的答解精度为同一量级)。

分别采用上述3种标定结果，对剩余的15个标志点Zi(i=1,2,3…15)用空间前方交会求得其物方三维坐标，并与VSTARS摄影测量系统测得的三维坐标进行公共点转换，所得坐标差值如表3所示。

从表3中的数据可以看出，基于岭估计的相机标定效果和基于抗差岭估计的相机标定效果明显优于基于最小二乘估计的相机标定效果，说明岭估计和抗差岭估计均能改善法方程系数阵的病态问题。基于抗差岭估计的标定效果略好于基于岭估计的标定效果，原因是抗差岭估计可以抵制观测值中粗差的影响，而岭估计没有抗差性。

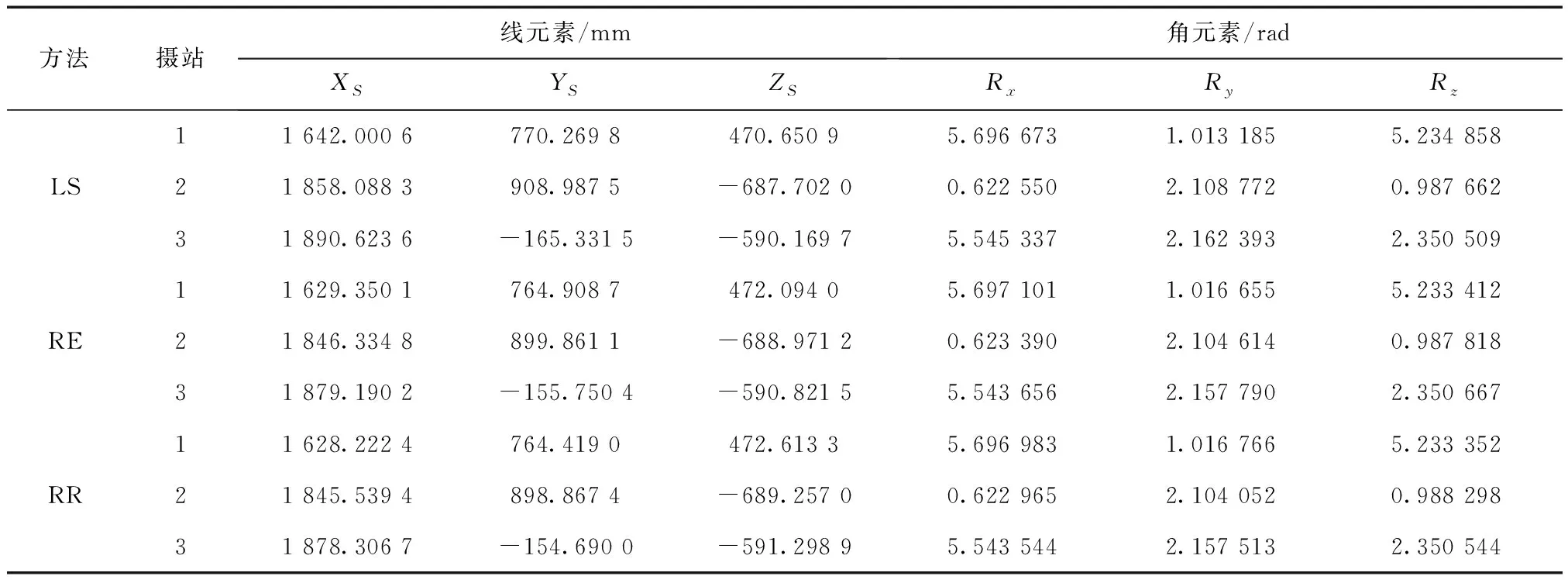
表1 相机外方位元素标定结果

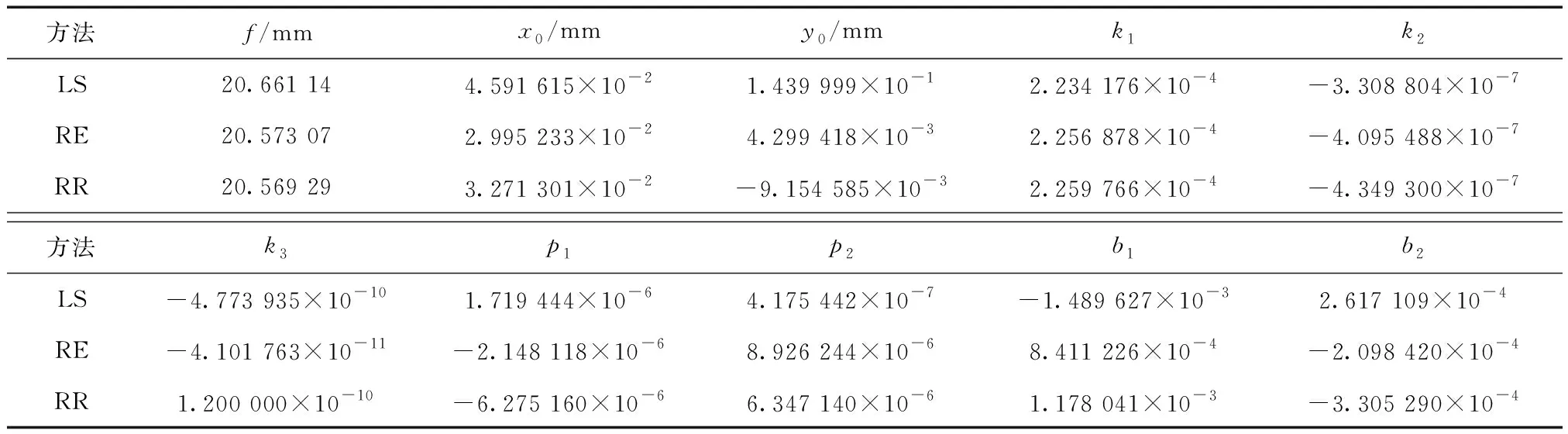
表2 相机内方位元素标定结果

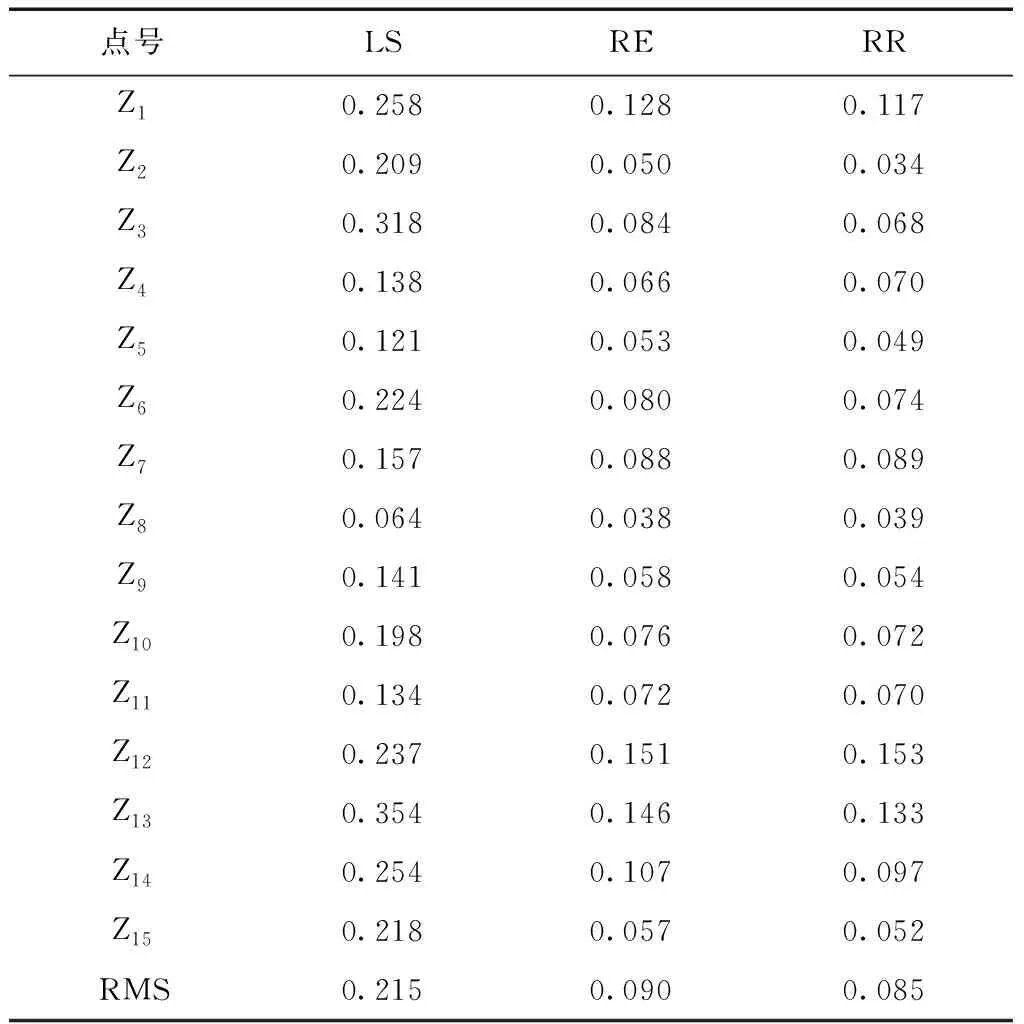
表3 公共点转换坐标差值 mm

4.2 模拟粗差实验

为了进一步检验相机标定模型受到观测异常时，基于抗差岭估计的相机标定的效果，在上述实验中选取3个像点观测值，分别加上5倍、10倍和15倍的单位权中误差后，再分别用最小二乘平差(LS)、岭估计平差(RE)和抗差岭估计平差(RR)3种方法进行标定解算，重复上述实验步骤，所得公共点转换的结果如表4所示。

从表4中的数据可以看出，在观测值中加入粗差后，用最小二乘平差和岭估计平差相对于加粗差前的标定效果明显变差(0.234对比0.215，0.108对比0.090)，而用抗差岭估计的标定效果基本不变(0.080对比0.085)。实验中发现，当增大加入的粗差后，最小二乘平差和岭估计平差的标定效果波动较大，说明受粗差影响较大；而抗差岭估计的标定效果基本稳定不变，说明受粗差影响较小。

对MetronIn-DPM软件处理得到的外方位元素初值进行不同程度的加减，得到3组不同的外方位元素初值。采用本文提出的基于抗差岭估计方法进行相机标定，均收敛到相同结果，说明本文提出的标定方法对参数初始值不敏感。

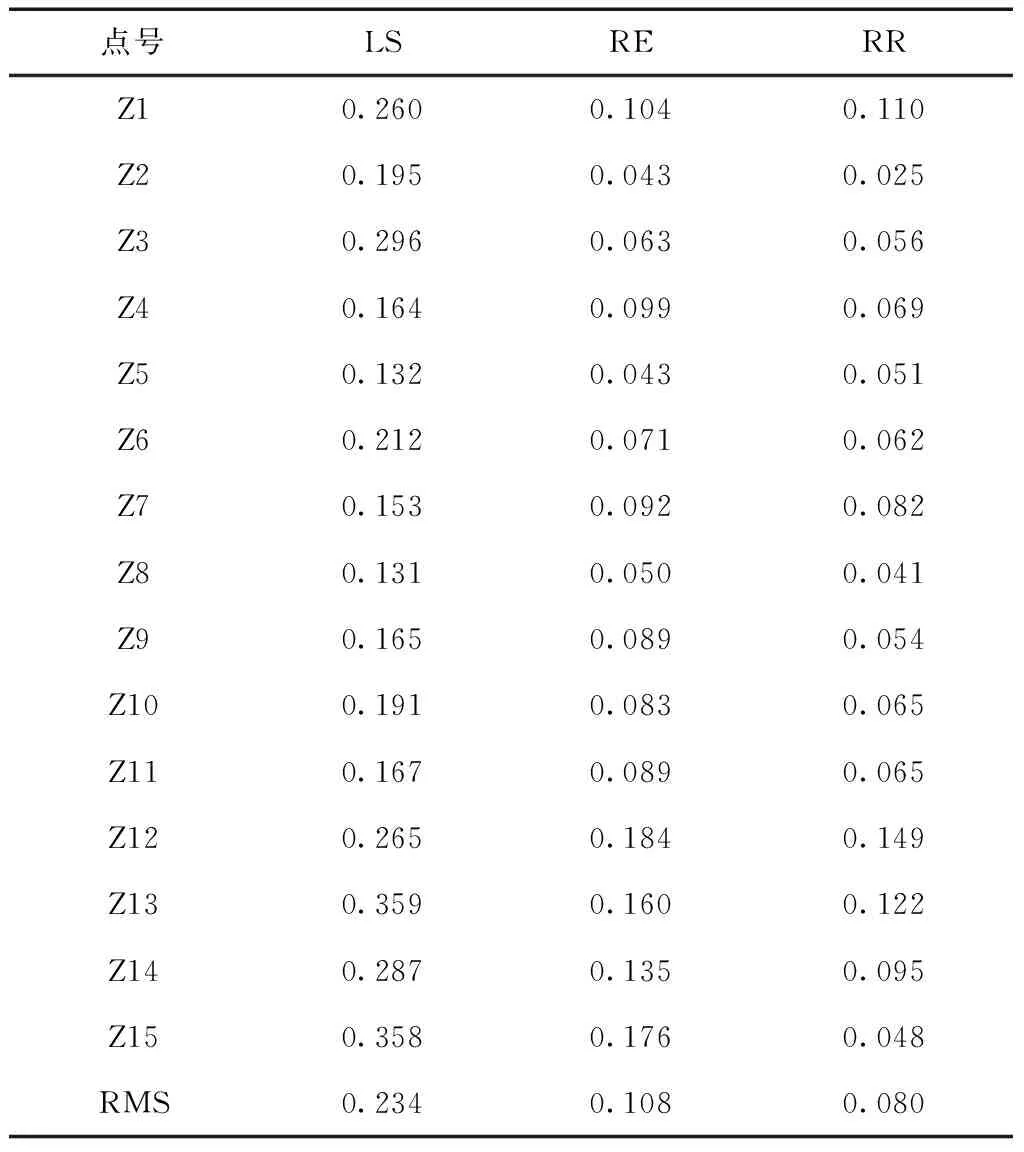
表4 公共点转换坐标差值 mm

5 结束语

本文提出基于抗差岭估计的相机标定方法，通过与基于最小二乘的标定方法和基于岭估计的标定方法的对比实验表明：基于抗差岭估计的相机标定方法能有效解决相机标定过程中的参数相关性问题，且有效抵制观测粗差的影响，使解算的参数结果更优。