相机与激光跟踪仪相对位姿标定方法的研究

范百兴，杨聚庆，周维虎，李祥云

(1.信息工程大学 地理空间信息学院，河南 郑州 450001；2.北京工业大学 应用数理学院，北京 100124；3.中国科学院光电研究院，北京 100094)

随着现代工业测量的需要，在航空、航天和装配等领域不仅需要对空间目标的位置进行精确测量，需要姿态信息，即目标的六自由度。长期以来，六自由度测量的方式多依赖于光学测量传感器、激光干涉仪[1]、多相机协作的视觉测量系统[2]，传统的六自由度测量方式仪器组合多、难以实现跟踪测量和使用复杂等缺点。

在现代精密工程测量中，激光跟踪仪具有在单点测量中的精度高、动态测量、实时快速等优点，在数字化设计、制造和装配检测中的应用越来越广泛[3]；视觉测量具有无接触、多目标、操作简便等优点，在研究物体的几何尺寸以及在空间中的位姿中的应用越来越广泛[4]。近年来，由于两者在测量中的优势，使两者的联合测量在六自由度精密测量中成为一种新的测量技术。在国外，leica T-mac是激光跟踪仪测量技术与视觉测量技术相结合的目标六自由度测量技术，实现目标六自由度跟踪测量[5]。而在国内此技术的相关文献较少，为了实现这种高精度、轻便的六自由度测量，必然存在着相机与激光跟踪仪位姿模型的标定。标定中所用的算法有：基于Canny算子的标志中心坐标提取；基于4个非共线控制点的单像空间后方交会；坐标系转换。坐标系转换的方法有奇异值分解、四元数法及罗德里格矩阵法[6]。奇异值分解的方法比较依赖于矩阵的性质，不一定得到旋转矩阵，特殊性较强，四元数解算速度较快，但是精度不容易控制，而罗德里格矩阵在任意角度的姿态转换解算中的严密性，在迭代中可以设置精度阈值，使用较为方便，因此本文在模型标定中采用罗德里格矩阵的方法。

1 相机坐标系下靶点坐标的解算

本文首先利用Canny算子对含有靶点的图像进行边缘检测，通过标志轮廓检测、模式识别、最小二乘拟合椭圆中心的方法得到标志中心坐标[7]，再由内方位元素得到靶点的像点坐标。最后通过一种基于4个非共线控制点的单张像片空间后方交会算法可直接求得单张像片的外方位元素[8]。算法流程如图1所示。

经过图像处理可以方便准确的得到靶点的图像像素坐标(ui,vi)，再由相机内部参数得到像点坐标：

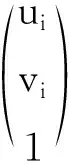
(1)

式中：u0，v0是相片尺寸长和宽的一半，dx，dy像素大小。在像点坐标的基础上，除了利用相机内参数的主距f和主点坐标(x0,y0)，还有镜头径向畸变(k1,k2,k3)、偏心畸变(p1,p2)及平面畸变(b1,b2)等7个内参数可以修正像点坐标，本文修正像点坐标的10参数模型为

(2)

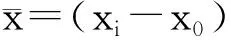
如图2所示，物方点A，B，C在激光跟踪仪下的坐标为(XL1,YL1,ZL1)，(XL2,YL2,ZL2)，(XL3,YL3,ZL3)，到相机中心S的距离分别为AS，BS，CS，相应像点坐标分别为A′(x1,y1)，B′(x2,y2)，C′(x3,y3);ΔABC边长分别记为AB，AC，BC;∠ASB，∠BSC，∠ASC分别记为α，β，γ。

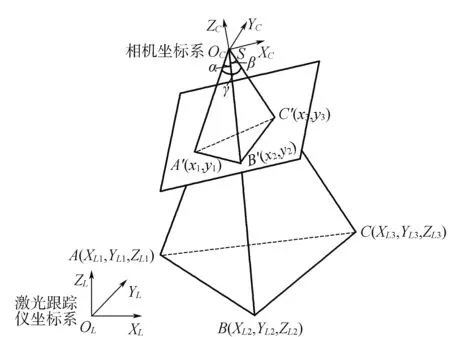
图2 利用4个控制点计算外方位元素

根据图中的几何结构及余弦定理可得

(3)

其中：

(4)

设AS∶BS∶CS=1∶n∶m，即BS=nAS,CS=mAS，将三者比例关系代入式(3)，消去AS，m整理得

w1n4+w2n3+w3n2+w4n+w5=0.

(5)

其中系数wi均可由物方点坐标，α，β及γ求得。该一元四次方程可能有4个根，再加一个靶控制点D，选取两组解中相同的根即为正确的n值。进而可得

(6)

在相机坐标系OCXCYCZC中，像点的坐标为A′(x1,y1,-f)，B′(x2,y2,-f)，C′(x3,y3,-f)，由图2知，根据AS与SA′、BS与SB′和CS与SC′之间的比例关系可得各靶点在坐标系OCXCYCZC中的坐标(XCi,YCi,ZCi)：

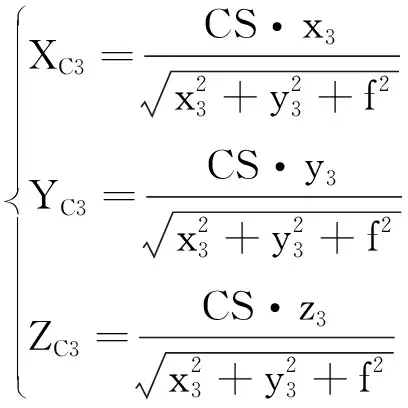
(7)

2 基于罗德里格矩阵的坐标系转换

当已知3个靶点在相机坐标系下和在激光跟踪仪坐标系下的坐标时，根据公共点求得相机坐标系和激光跟踪仪坐标系的位姿转换矩阵。当多于3个靶点时，公共点转换一般需要先求初值再进行平差迭代[9]，本文利用基于罗德里格矩阵的方法求解转换参数。

设相机坐标系和激光跟踪仪坐标系的位姿转换矩阵为Tr,

.

(8)

由靶点分别在两坐标系中的坐标可得

.

(9)

其中R,T分别是位姿转换矩阵Tr中的旋转矩阵和平移矢量。本文利用3个控制点求解旋转矩阵和平移参数的初值。其中R用罗德里格矩阵表示

R=(I-S)-1(I-S).

(10)

其中I为单位阵，

.

(11)

,(i=1,2,3).

(12)

其中，

.

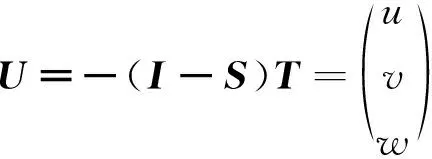
(13)

将式(13)代入式(12)得

.

(14)

由式(14)可知，n对公共点对应3n个观测方程，将其写成矩阵形式为

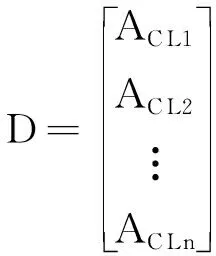
(15)

其中

，

艾滋病可经过母婴传播、性传播以及血液传播等，机体感染艾滋病病毒后引发病毒血症，病毒在咨询者肝细胞内复制并引发病变，此外，艾滋病病毒表达产物存在肝脏毒性，会导致肝功能下降。若咨询者艾滋病抗体实验室检查结果为阳性、近期有流行病史，则可诊断为艾滋病急性期[4] 。大部分艾滋病感染咨询者在感染2个月后即可检出艾滋病抗体，感染后3个月可全部检出艾滋病抗体。当前，我国主要通过疫苗预防艾滋病感染，同时加强艾滋病宣传，及时发现艾滋病并采取病情控制措施，有助于使艾滋病毒损伤得到控制并可使病毒传播得到减少[5] 。

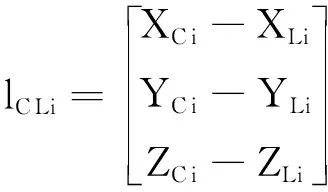
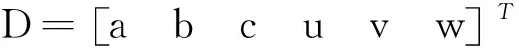
(16)

当n=3时，此时没有多于观测量，直接求解D，那么：

D=(AT·A)-1·(AT·l).

(17)

将解得的a，b，c，u，v，w作为D的初值D0，并将其余公共点代入式(15)组成观测方程，

A·(D0+ΔD)=l.

(18)

进而求改正值，

ΔD=(AT·A)-1·[AT·(l-A·D0)].

(19)

判断此时改正值是否小于阈值ε，否则代回式(17)修正初值D0，并继续求解修正值直到满足阈值条件。最后，将经过迭代后的D0代入式(10)、式(11)和式(13)可求得位姿变换矩阵R,T。

3 算例和分析

3.1 数据采集与预处理

测量过程使用的工业相机为basler ACA 2500-20 gm，镜头为computer m0814-MP，CCD成像个数为(2 592像素×2 048像素)，像素大小为 0.004 8 mm×0.004 8 mm。首先对相机内参数进行标定，利用教研室标定场，采用基于有限元模型的数字工业摄影测量相机二次检校的方法检校相机[10]，标定结果为:x0=-0.128 630 6 mm，y0=0.202 353 3 mm，f=11.860 89 mm，k1=7.659 920×10-4，k2=-4.942 919-6，k3= 3.922 201-9，p1=-6.417 617-6，p2= -2.753 530-6，b1=-6.517 062-6，b2=-5.578 664-5；使用的激光跟踪仪为Leica AT901-B型,配合CCR1.5角隅棱镜靶球,在2.5 m×5 m×10 m的工作范围内三维点坐标测量精度为±(15 μm+6 μm/m)。

首先在试验场布置5个靶座，靶座上既可以放置角隅棱镜靶球也可以放置人工标志工装，激光跟踪仪所测靶球中心和视觉测量的标志中心理论上为同一点；然后将人工标志工装放置于靶座上，用固定好的相机采集包含人工标志的图像，随后撤掉人工标志工装并用激光跟踪仪(配合靶球)测量靶座中心坐标；最后用罗德里格矩阵进行坐标系转换。

对采集到图像首先利用Opencv中Canny算子对标志进行检测边缘，并用椭圆拟合算法求出圆形标志的中心坐标，此时坐标为图像像素坐标系下，需由式(1)转换为像平面坐标系下，结果如表1所示。

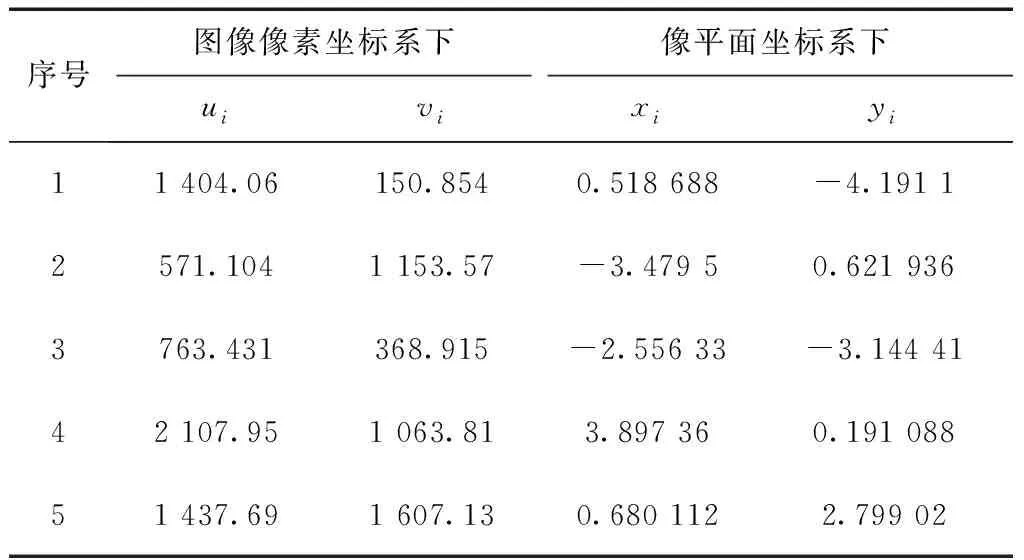
表1 椭圆拟合得到的标志中心坐标 mm

利用激光跟踪仪和靶球分别测量各个靶座上的中心坐标，得到坐标结果如表2所示。

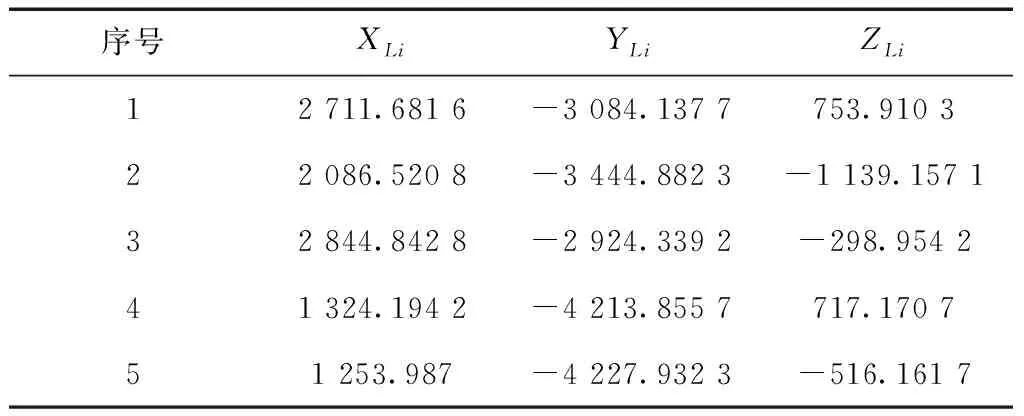
表2 跟踪仪坐标系下各靶座中心坐标 mm

通过测量和预处理，表1为经过预处理后的数据，表2为激光跟踪仪直接测量所得到的数据。在所采集数据基础上即可进行坐标系转换和精度分析。

3.2 坐标系转换和精度分析

在对应的5组坐标中选取4组作为求解坐标系转换参数的数据，为了保证4点非共线以及各靶点与相机中心S的连线之间的夹角尽量大，实验所用点号分别为1、2、3以及4，根据相机坐标系下靶点坐标的解算理论，可能会解出两组相近的n值，利用两组n值分别求出坐标系转换参数，进而利用共线方程反算像点坐标，反算结果与表1进行比较，结果相近的为正解，结果如表3所示。

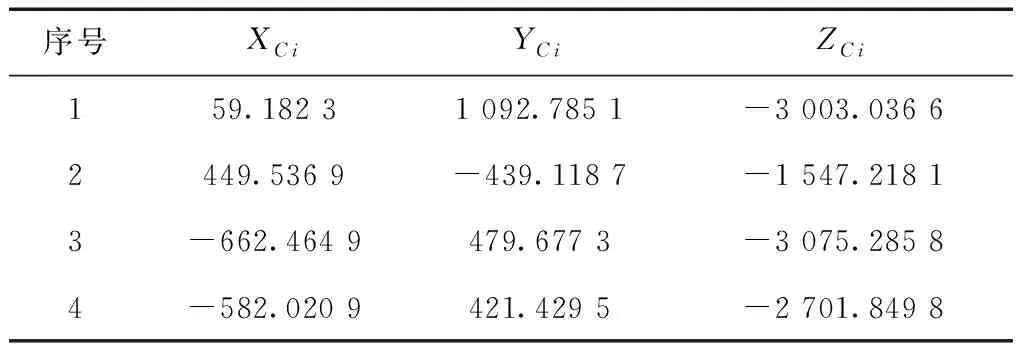
表3 靶点在相机坐标系下的坐标 mm

利用表2和表3中4组对应的公共点，用罗德里格矩阵进行坐标系转换，先用其中3组数据解算转换参数的初值，利用初值和全部数据进行最小二乘迭代，直到平差精度满足设定阈值为止。最终所得跟踪仪与相机相对位姿模型为

(20)

为了验证坐标系转换精度，本文利用矩阵T及共线方程反算像点坐标，将结果与椭圆拟合所得结果进行比较，比较结果如表4所示，

(21)

表4仅仅为相机在某一个位姿下的标定精度，为了说明算法的普适性，将相机调整位姿继续拍摄两张照片，标定结果如表5和表6所示。

综合表4、表5和表6得计算结果，位姿标定模

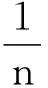
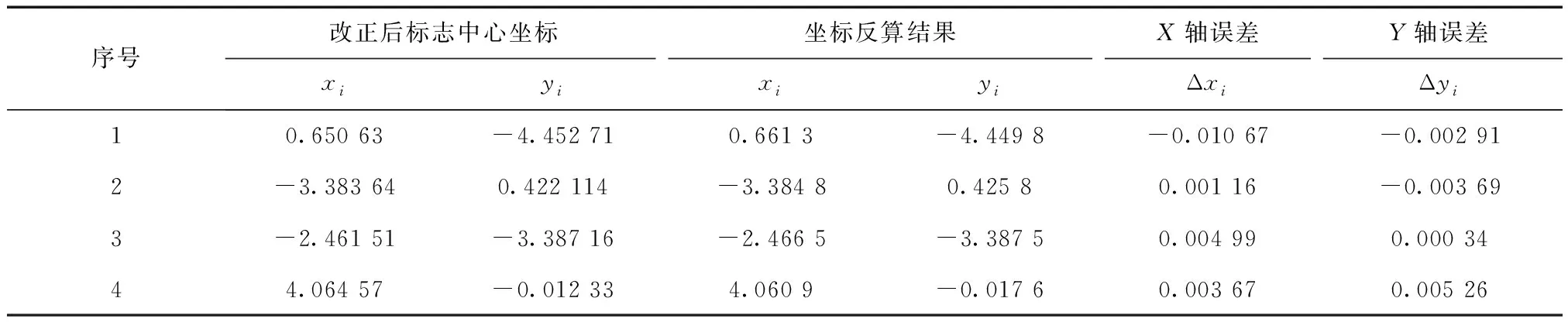
表4 坐标反算结果与椭圆拟合坐标对比表 mm

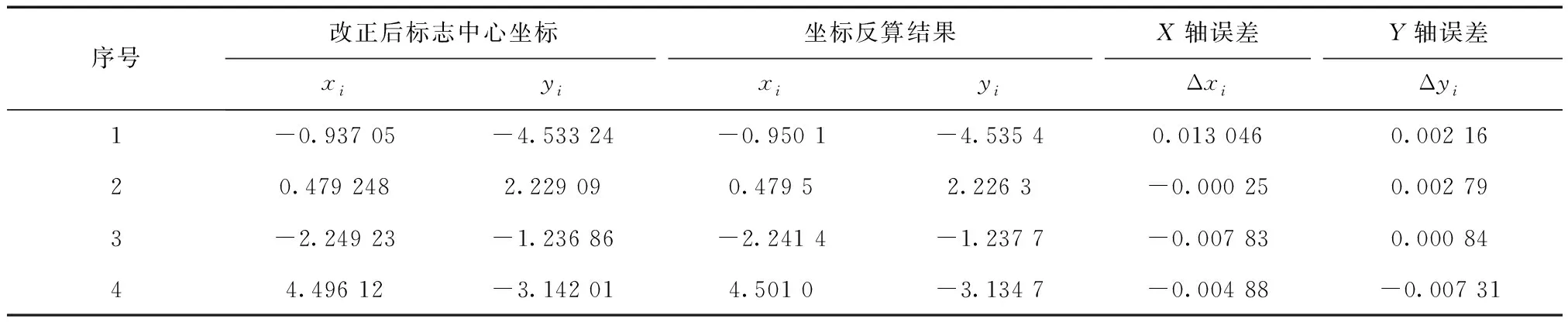
表5 相机位姿一次调整后的标定结果 mm

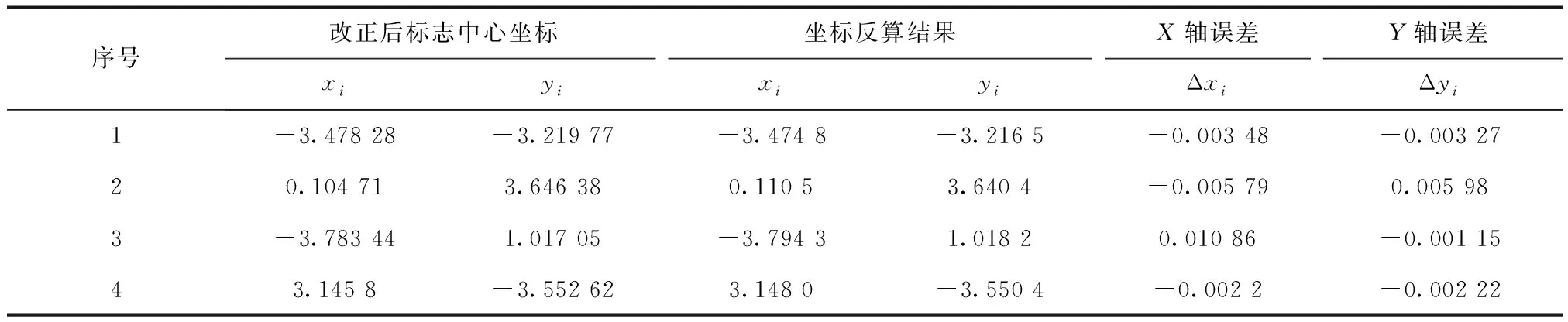
表6 相机位姿二次调整的标定结果 mm

4 结 论

在六自由度精密测量中，针对激光跟踪仪与视觉测量联合应用中的相机与激光跟踪仪相对位姿的标定问题，本文利用基于罗德里格矩阵的方法标定了两者之间的相对位姿以及利用共线方程反算标志中心坐标验证了转换精度。实验结果证明，所得相机坐标系与激光跟踪仪相对位姿模型总体精度保持在0.01 mm以下，基本满足了激光跟踪仪与相机联合精密测量中的需要。