非差模型与双差模型的定位精度比较

崔 阳，苗亚哲，辜文杰，杜伟平，魏佼琛

(1.陆军勤务学院，重庆 401331； 2.信息工程大学，河南 郑州 450052)

以美国全球定位系统(Global Positioning System, GPS)、中国北斗导航卫星系统(BeiDou Navigation Satellite System，BDS)等为代表的全球导航卫星系统(Global Navigation Satellite System, GNSS)在交通运输、航空航天等领域得到了广泛应用。在GNSS精密数据处理中，以双差模型为基础的基线网解模式是常用方法之一[1-4]，但随着多频多模和测站规模增加，基线网解计算时间呈指数级上升。为了打破双差网解模式的计算瓶颈，有学者提出了以非差模型为基础的精密单点定位(Precise Point Positioning, PPP)模式[5-7]，其单站处理模式即可获得测站绝对坐标，计算效率高，显著降低了大网数据处理的计算时间。文献[8]从理论上证明了双差网解和PPP解的模型等价性，文献[9]对非差与双差模型进行了对比，指出非差模型通过精确的误差改正可实现厘米级甚至毫米级的静态定位结果。作为高精度GNSS数据处理中常用的两种数学模型，虽然许多学者在理论上证明了双差模型和非差模型的等价性，但由于误差源的改正通常是采用经验模型，且非差模型直接得到绝对坐标而双差模型需要引入坐标基准才能获得绝对坐标，对于精度要求较高的参考框架维持、地壳运动和变形监测等应用领域，非差模型或双差模型进行数据处理是否精度一致还需进一步研究验证。本文选取国际地球参考框架(International Terrestrial Reference Frame, ITRF)核心站组建长度不同但相对位置长期不变的基线，数据采取单站模式进行相同的预处理策略，仅在误差方程建立时分别采用非差模型与双差模型，对连续一年的数据分别进行非差定位解算和双差定位解算，以“相对坐标”作为比对值分析两种模型之间实际定位精度的差异性。

1 模型比较

以无电离层组合值作为观测值，其消除了载波和测码伪距上的电离层一阶项，电离层组合模型的非差观测方程为：

(1)

假设卫星轨道和钟差已知，对流层延迟表示为天顶延迟和投影函数的乘积，即T=zhd×Mh(θ)+zwd×Mw(θ)，其中zhd和zwd分别为天顶流体静力学延迟和天顶湿延迟，Mh(θ)和Mw(θ)为静力学映射函数和湿映射函数，天顶湿延迟zwd作为参数估计，则以消电离层组合作为观测值的非差函数模型：

(2)

双差观测模型通常是先在站间单差，然后选取基准星后再进行星间双差。假设测站r1和r2同时跟踪GPS卫星，对卫星s1、s2的载波相位和伪距无电离层组合的双差观测方程：

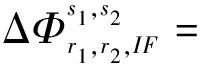
(3)

(4)

GNSS精密数据处理流程如图1所示，包括文件读取、数据预处理、误差改正、参数估计与结构输出等5个模块。图1中原始GNSS观测值中包含各种误差，只有消除或者改正误差影响，才能实现静态厘米级甚至毫米级的定位结果。GNSS数据处理中的误差改正如卫星钟差、卫星天线相位中心偏差、相位缠绕效应、卫星钟相对论效应、接收机天线相位中心改正、天线归心改正、地球固体潮改正、海洋负荷潮汐改正、极潮改正、地球自转改正、对流层延迟等，一般采用数学模型或经验公式进行改正，而接收机钟差、对流层湿延迟等通常作为待估参数进行平差处理。非差模型与双差模型从理论上分析是等价的[8]，但实际数据处理中，非差模型中需要详细而准确的误差改正方法，而双差模型利用观测的同步卫星通过对站、星间组差进行解算，可以消去卫星钟差、接收机钟差和硬件延迟小数部分，消弱或消除共性误差项的影响。

图1 GNSS数据计算流程图

为了比较双差模型与非差模型实际定位结果的差异，在图1的数据处理流程中，对两个测站采用双差模型或非差模型进行定位解算时，在文件读取、数据预处理和误差改正环节均逐测站进行，采用完全一致的精密星历产品、周跳探测算法、误差改正模型等，仅在参数估计环节中分别建立非差观测方程和双差观测方程。由于非差模型得到的坐标参数直接是绝对坐标，而双差基线得到的坐标参数是相对坐标，必须引入坐标基准进行基线网平差才能得到绝对坐标。如果比较绝对坐标值，则双差模型引入基准的精度影响两者等价性的判断。因此，本文先对基线的两个测站采用非差模型逐测站组建非差方程进行定位解算，得到测站坐标后反算得到两个测站的相对坐标值，将其与双差模型得到测站间的相对坐标值进行对比，避免基准精度对两种模型定位精度等价性分析的影响。

2 实验与分析

选取ITRF核心站组成长度不同但相对位置长期不变的基线，分别是STJO-STJ2、ZIMJ-WAB2、ALGO-NRC1、HERS-WSRT 4条基线(基线长度分别是42 m、5 194 m、198 574 m、487 618 m)，所选测站均是参与ITRF08框架建立的核心站(除了STJO站)，表1是从ITRF网站(itrf.ensg.ign.fr)查询各站在2013-01-01的ITRF08框架下的坐标值和年运动速度，各基线的测站板块运动速度基本相同，则基线的相对坐标值可认为始终保持不变，其中STJ2不在ITRF2008中，但由于与STJO站相距42 m，可认为年速率与STJO站相同。对4条基线2013年全年数据进行非差模型和双差模型定位解算，比较双差解与非差解的相对坐标结果的差异。由于部分测站某些天观测数据缺失，如ZIMJ测站前120天没有数据，本文仅对有效天数的数据进行解算。

表1 在历元2013/01/01时ITRF2008框架下的测站坐标和速度信息

以无电离层组合值为观测值，采用IGS发布的15 min精密星历和5 min钟差的最终产品改正轨道和卫星钟差误差，所有cm级以上的误差均进行改正，参数与模型设置如下表2。双差计算策略中数据预处理也是以站为单位进行单站预处理，与非差计算策略中预处理过程完全一致，两中处理方式仅在矩阵构建和解算过程不同。为避免过度参数化，对于超短基线STJO-STJ2双差解算时，不估计对流层湿延迟参数。

表2 参数与模型设置

图2为非差与双差模型计算得到的各基线在XYZ3个方向的相对坐标值，其中“DD”表示双差模型，“UD”表示非差模型。进一步对全年的各个方向的相对坐标值序列计算其平均值和标准偏差，如表3所示。

表3 不同基线的非差与双差解时间序列的平均值和标准差

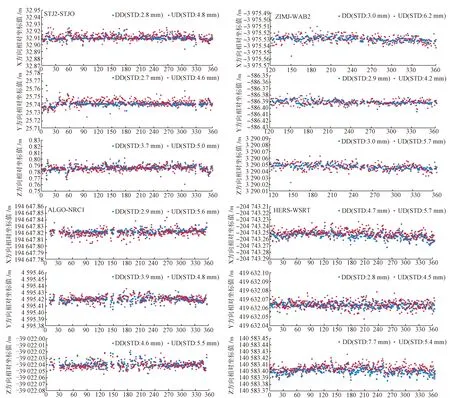
图2 非差与双差解算基线的不同方向的相对坐标值分量序列

分析图2和表3可知，非差解的全年的相对坐标时间序列标准差的均值是(5.6,4.5,5.4) mm，而双差解是(3.4,3.1,4.0) mm，双差模型的解算精度和稳定性整体优于非差模型。随基线的增长，双差模型差异呈现累积性，而非差模型差异基本没变化，如42 m超短基线STJ2-STJO全年数据非差解和双差解的标准差分别为(6.2,4.8,5.7) mm和(3.0,2.9,3.0) mm，而487 km长基线HERS-WSRT则是(5.7,4.5,5.4) mm和(4.7,2.8,4.7) mm。短基线情况下，双差模型能够有效消弱或消除观测误差，定位解算比非差模型更加稳定，从图2中更能直观看出双差解算的坐标序列更加集中稳定。随着基线增长，空间误差的相关性减弱，双差模型的偏差累加，其稳定性降低，但依然优于非差模型，如487 km的基线HERS-WSRT全年数据的非差模型的坐标序列标准差为(5.7,4.5,5.4) mm，而双差的坐标序列标准差为(4.7,2.8,4.7) mm。

图3 非差与双差解算基线的相对坐标值在不同方向差值

表4 不同基线非差与双差解的偏差平均值和标准差

进一步对4条基线的双差与非差解算得到相对坐标值在X、Y、Z方向分别进行作差，差值如图3所示，全年差值平均值和标准差如表4所示，非差解与双差解在XYZ方向全年坐标分量互差的标准差均值是(5.2,4.6,4.4) mm，三维坐标偏差标准差达到8.2 mm，表明非差解与双差解存在定位偏差，但非差与双差模型解算结果不存在系统误差，如STJ2-STJO偏差值的平均值为(-1.2,-2.0,0.2) mm，标准差为(4.2,4.3,3.9) mm。理想状态下GPS的相位观测噪声为2～3 mm，计算的最好精度约为几个mm，而实际数据处理中，由于误差改正模型不精细和计算方法不完善等因素，解算结果的误差会更大。本文所编写的GNSS数据处理软件[10-11](www.gnsser.com)中对定位误差采用表2所列的模型改正方法，但对光压模型、高阶电离层改正等暂未考虑，算例中的精度并不具有普遍代表，但由于非差处理与双差处理仅是在方程建立与参数解算设置不同，因此，算例可以反映出双差模型在精度稳定性上比非差模型具有一定优势，特别是短基线情况下。

3 结 论

非差解和双差解从理论上是模型等价的GNSS数据处理方式，但实际数据处理中，误差改正模型目前大多是采用经验模型，而测站的环境(温度、湿度、气压、板块运动)等是动态变化的，误差改正模型不够精细和计算方式不够完善等因素，导致实际解算中非差模型与双差模型存在差异性。通过对长度不同但相对位置不变的基线一年的数据进行非差与双差定位解算，统计分析相对坐标分量偏差序列得知，非差解与双差解存在定位偏差，其三维坐标偏差标准差达到8.2 mm；通过对相对坐标时间序列的标准差分析表明，双差解算的定位精度和稳定性整体优于非差解算；但随基线的增长，特别是超过2 000 km的超长基线，双差模型的差异呈现累积性，而非差模型的差异基本没变化。

随着全球连续运行参考站网布设密度加大，GNSS基准站数越来越多，即便是全球网中也很少有超长的基线，而且计算机的性能也得到飞速提升。虽然非差模式解算效率快，但需要准确的误差改正模型，而双差模型可以有效地削弱或消除同类误差源。因此，在大网参考框架维持、变形监测等高精度应用领域，可优先考虑采用双差模型进行数据解算或者以非差模型的结果作为双差模型的先验信息，再采用双差模型进行联合解算。