基于二分法迭代的凸模数控铣削加工编程*
王华东
(辽宁轨道交通职业学院, 辽宁 沈阳 110023)
0 引 言
数控加工因其精度高、效率高和自动化程度高而被广泛应用于现代化加工生产中[1-2]。模具零件形状复杂,要求的精度高,所以模具零件的加工离不开数控加工。文章以模具加工中典型的凸模零件为研究对象,详细阐述了零件中特殊点的坐标值的求解,进而完成了该凸模零件数控铣削加工的程序编制。
1 数学模型建立
凸模零件形状尺寸如图1所示。

图1 凸模零件图
由圆弧和线段构成,数控编程是根据各个特殊点坐标值编写加工程序的,图1中求得两段圆弧(R=40 mm和R=8 mm)切点和圆弧(R=8 mm)与线段切点的坐标值是一个复杂的过程,可以借助二维绘图软件将凸模的零件图绘制出来,再标注其坐标值尺寸,但缺点是一旦该凸模的尺寸重新设计,就需要重新绘制零件图,再标注其坐标值尺寸;也可以根据切点的解析几何性质,列方程组求得坐标值,利用编程软件编写方程组求解器,无论尺寸怎么变化,只要在求解器中输入参数,即可求得切点坐标值。本文采用列方程组,再编写方程组求解器求得切点坐标值的方法。
该凸模零件的数控铣削加工以零件的上表面的中心为对刀点,所以建立了如图2所示坐标系,由于对称性,取右1/2图形为研究对象,设两段圆弧的切点坐标值为D(x1,y1),圆弧O1的圆心坐标为O1(0,50),点属于圆弧O1上的点,那么一定有:
x12+(y1-50)2=R12
(1)
设圆弧O2的圆心坐标为O2(50-R2,y2),点D(x1,y1)又属于圆弧O2上的点,那么也一定有:
(x1-50+R2)2+(y1-y2)2=R22
(2)

(3)
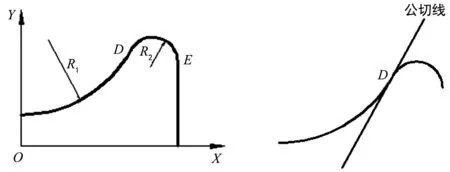
图2 计算图 图3 两段圆弧的公切线


设圆弧O2与线段切点坐标值为E(50,y3),根据圆弧与直线相切的几何性质可知:y3=y2。
2 程组求解器
随着计算机技术的发展,计算器因其方便快捷,而越来越受到人们的喜爱[4]。在编程软件中编制方程组求解器,程序如下:
Private Sub Command1_Click()
r1 = Val(Text1.Text)
r2 = Val(Text2.Text)
i = 1
x3 = 50 - 2 * r2
x4 = r1
X1 = (x3 + x4) / 2
Y1 = 50 - Sqr(r1 ^ 2 - X1 ^ 2)
Y2 = Y1 - Sqr(r2 ^ 2 - (X1 - 50 + r2) ^ 2)
Do Until Abs(X1 / (50 - Y1) - (X1 - 50 + r2) / (Y2 - Y1)) < 0.0000000001
DoEvents
If X1 / (50 - Y1) - (X1 - 50 + r2) / (Y2 - Y1) > 0 Then
x4 = X1: X1 = (x3 + x4) / 2
Else
x3 = X1: X1 = (x3 + x4) / 2
End If
Y1 = 50 - Sqr(r1 ^ 2 - X1 ^ 2)
Y2 = Y1 - Sqr(r2 ^ 2 - (X1 - 50 + r2) ^ 2)
i = i + 1
Loop
Text3.Text = Format(X1, "0.###") & "," & Format(Y1, "0.###")
Text4.Text = i & "次"
Text5.Text = "50" & "," & Format(Y2, "0.###")
End Sub
Private Sub Command2_Click()
End
End Sub
生成的方程组求解器界面如图4所示, 在对象窗口中,添加输入两个文本框,分别输入两段圆弧半径值;添加三个输出文本框,分别输出点D、E坐标值和二分法迭代计算次数。
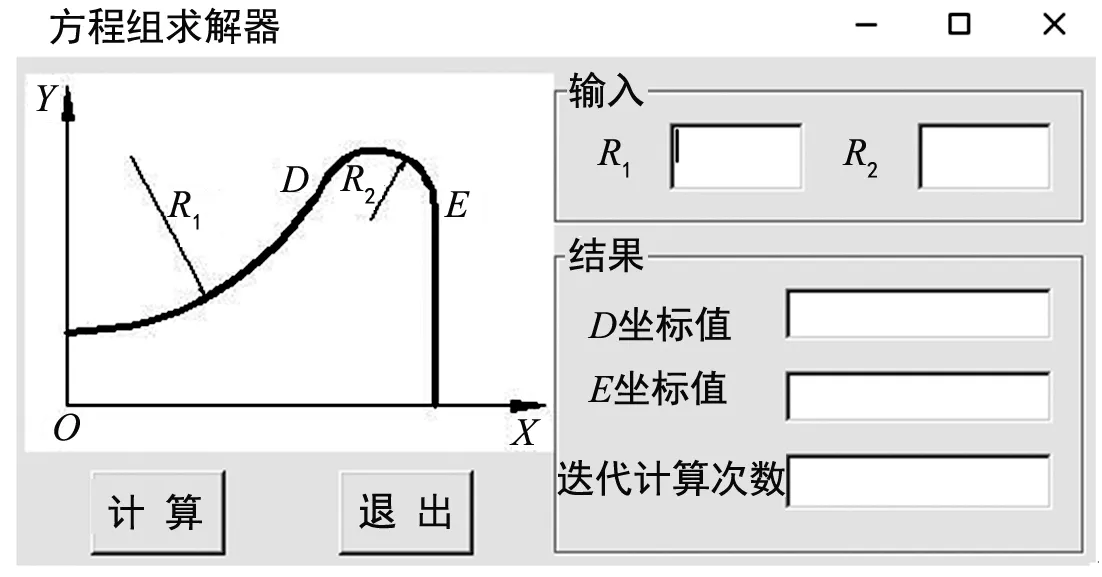
图4 方程组求解器

图5 计算结果
3 数控程序
在输入文本框中R1=40,R2=8,计算后的结果如图5所示。经过35次迭代计算,求得两个圆弧切点D(35,30.635),圆弧与线段切点E(50,26.762)。
选用Φ10立铣刀,在华中数控铣床中编程如下:

%1010;文件名G17G54G90;初始化M03S800;主轴正转G00X-50Y-80;Z5;G01Z-2F50;G41G01Y-50D01;建立刀具半径补偿Y26.762;G02X-35Y30.635R8;G03X35R40;G02X50Y26.762R8;G01Y-40;G02X40Y-50R10;G01X-40;G02X-50Y-40R10;G01Z5;G40G00X100Y100;取消刀具半径补偿M05;主轴停M30;程序结束返回程序头
在数控铣床中,多次设定刀具半径补偿值和Z方向下刀深度值进行加工,完成凸模零件的数控加工。
4 结 语
根据凸模零件特殊点的解析几何性质,列出了非线性方程组,在编程软件中编制了方程组求解器 ,输入相应参数,即可求得各切点坐标值 ,方便快捷。根据得到的切点坐标值 ,编写了数控铣削加工程序。

