一道几何证明题的方法与研究
牛 鑫
(辽宁省大连市第七十六中学,辽宁 大连)
初中几何是数学学习的重要内容。学好几何不仅对于初中数学的学习有极大的帮助,而且对高中数学的学习也有一定影响。几何学更能够培养学生的逻辑思维及抽象思维能力。但多数同学感觉证明几何题时没有思路,特别是对一些需要添加辅助线的几何题感到无从下手,因而失去了学习几何的信心。因此教给学生解题思路和解题技巧是帮助学生提高分析问题、解决问题能力的关键。下面就以一道2014辽宁大连一模几何证明题的某一问来探究如何分析几何证明题,采用构造法解决几何证明题。
问题:(2014辽宁大连一模)如图1,△ABC中,AB=AC,点D在BC上,点E,F分别在AD和AD的延长线上,且∠AEC=∠BAC,BF∥CE.
(1)求证:∠AFB与∠BAC互补
(2)图1中是否存在与AF相等的线段?若存在,请找出,并加以证明,若不存在,说明理由。

图1
探究两条线段之间的数量关系,一般都需要通过构造两个三角形全等来实现。如何添加辅助线,利用已有的边和角去构造出全等的三角形,以及怎样证明两个角相等,这些几何问题的证明思路学生比较陌生,解决这些问题的方法都需要逐步在课堂渗透,引导学生不断感悟,并将学会的方法进行迁移。
多种解法,一个思想
【证法 1】(1)如图 2,∵BF∥CE,∴∠AFB=∠CEF
∵∠CEF与∠AEC互补,∠AEC=∠BAC,
∴∠CEF与∠BAC互补.∴∠AFB与∠BAC互补
(2)存在,CE=AF.
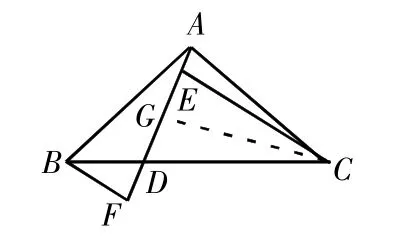
图2
如图2,在AF上取一点G,使AG=BF
∵∠AFB+∠BAC=180°=∠AFB+(∠BAF+∠CAF),
∠AFB+∠ABF+∠BAF=180°,
∴∠ABF=∠CAF
又 ∵AB=AC,∴△ABF≌△CAG
∴AF=CG,∠AFB=∠CGA
又 ∵∠AFB=∠CEF,∴∠CGA=∠CEF.
∴CE=CG.∴CE=AF.
【点评】证明线段CE与AF相等,可以转化为证明包含CE边的三角形与△ABF全等,通过挖掘已知条件,发现∠ABF=∠CAF,又AB=AC,这时还缺一个条件,于是从SAS(边角边)证明三角形全等切入,在AF上截取AG=BF。从一条对应边相等,一组对应角相等入手,再构造一组对应边相等,这样便可构造出一对三角形全等。
下面在该题的其余解法中选择两种供参考。
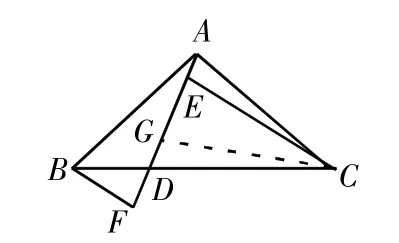
图3
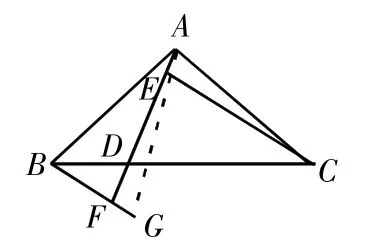
图4
【证法2】如图3,构造与△ABF全等的三角形。在AF上取一点 G,使得 CG=CA,则 CG=BA,∠CGA=∠CAG,而∠GAC=∠ABF,所以∠CGA=∠ABF,又 BF∥CE,则∠BFA=∠CEG,从而△ABF≌△CEG,所以CE=AF。此方法的关键是通过作等腰构造出与∠CAG相等的角。
【证法3】如图4,我们也可以构造与△ACE全等的三角形。根据同角的补角相等,则∠AFG=∠AEC。可以考虑从这对角相等入手,还需要引入一条辅助线,既能带来边相等也能带来角相等,于是在BF的延长线上取一点G,使得AG=AB,即构造等腰三角形来实现。
我们发现遇到两个角互补的问题,可以通过构造已知边的等腰也可构造求证边的等腰,从而为证明三角形全等作准备。在作辅助线的过程中,注意不要破坏题目中原有的条件。
构造思想是数学思想的一种思考方式,而构造法是数学方法中的一种。构造性的思想决定了如何构造,怎么构造,构造后怎么解决等问题。构造法是根据原问题的条件和结构来进行分析观察,然后通过联想原有的知识进行迁移变换,由于每个人的知识层次不同,解题经验不同,思考的方向不同,这也决定了形式也是不同的,所以构造法的灵活性很大,一个问题可能有多种不同的构造方式。
通过上面的分析可以知道,在探究两条线段之间的数量关系时,我们可以从一边一角即一组边对应相等,一组角对应相等,通过辅助线构造出一个三角形与确定的另一个三角形全等。但值得注意的是,在证明角相等的问题时,暴露出学生的不足之处,需要引导学生进一步总结推理角相等的方法,需要我们在课堂上给予学生充分的时间和空间,进一步来完善学生的几何证明推理能力。
我们所给出的各种思路能帮助学生进行构造性思维的训练和理解,同时让学生从本质上理解构造法的意义,并且在训练中提高学生的创新能力。构造法需要学生有良好的知识框架,才能建立起知识之间的内在联系,才能更好地进行构造,所以要将所学的知识系统化、有序化,经常整理知识,分析它们之间的内在联系,建立良好的知识框架才能培养出好的构造思想。

