注重教学过程设计，提高学生课堂参与

唐露溢

（四川省犍为县罗城初级中学，四川 犍为）

2004年12月25日，教育部正式颁布了《中小学教师教育技术能力标准》，它的实施使中小学教师的专业能力有了第一个标准。在《中小学教师教育技术能力标准》中对教学设计的定义为：教学设计又称为教学系统设计，是指主要依据教学理论、学习理论和传播理论，运用系统科学的方法，对教学目标、教学内容、教学评价等教学要素和教学环节进行分析、计划并作出具体安排的过程。对教师的能力有很多要求，而且每个要求之间有着千丝万缕的联系，不可分割，但我想着重谈谈教学过程设计能力。

一、具有层次，节奏流畅

教师在教学过程中根据每个班同学的理解程度、知识基础，由浅入深、循序渐进，控制好层次，把握好节奏，可以让沉闷的教学更有活力，让学生更想参与，更容易参与。

案例一：华东师大版七年级数学上册已经让学生开始接触整体代入法，但是如何让学生容易理解整体的思想，并转化成运用，每个教师根据自己的经验和自己学生的情况都有一套自己的套路。以下是我给七年级学生讲整体代入法的步骤。

步骤一：练习：若 A=4，B=3，则 A2-2B=_________。

步骤二：探索：例 1：若 m+n=4，mn=3，求（m+n）2-2mn的值。模仿例1自己编写一道相似的题。

步骤三：练习 2：已知 a、b 互为相反数，c、d 互为倒数，求 2（a+b+cd）的值。

步骤四：例2：若a-3b=-3，则代数式5-a+3b的值为___。

步骤五：例3：若x+5y=4，求代数式2x+10y+7的值。

步骤七：我想和___做对手。我为他出的题是___。

学生通过层层抽丝剥茧的学习，体验到成功的喜悦，积极地参与到活动中，体现自己的价值。

二、符合学生学习规律

学生的认知都是由浅入深、由具体到抽象、由感性到理性，但是不同的学生认知也有不同，所以对同一事物的看法也会不同。在教学过程中，根据自己对学生的了解，制定符合自己学生的教学过程，让学生在课堂上喜欢参与。

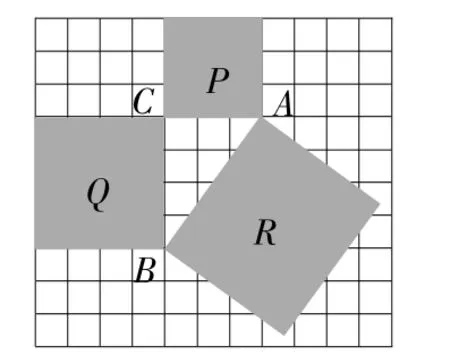
案例二：华东师大版八年级数学上册第14章勾股定理中，为了引入勾股定理先研究直角三角形三边的关系。

试一试：观察图，如果每一小方格表示1平方厘米，那么可以得到：正方形P的面积=___平方厘米，正方形Q的面积=___平方厘米，正方形R的面积=___平方厘米，我们发现，正方形P、Q、R的面积之间的关系是___。由此，我们得出Rt△ABC的三边长度之间的关系是____。概括出勾股定理以后再根据弦图用面积进行证明。

三、活动目标适度且有吸引力

学生千差万别，层次不一，深入地了解自己的学生，在教学中建立适合他们的教学要求和目标，让他们跳一跳就能完成学习任务，学生内心充满成就感，让刻板的数学吸引他们参与其中。有一部分学生由于小学时期对于算数思想根深蒂固，在学习代数时不容易转变，针对这部分学生，如果先用数字再用字母，会让他们在学习中更容易接受，更有兴趣，能主动参与，完成教学目标。

案例三：探索百分率问题：

探索：1.某产品去年的产值为100件，今年的增长率为20%，则今年的产值为100（1+20%），如果明年的增长率也为20%，明年的产值为 100（1+20%）（1+20%）=100（1+20%）2

2.某产品去年的产值为a件，今年的增长率为x，则今年的产值为 a（1+x），如果明年的增长率也为 x，明年的产值为 a（1+x）（1+x）=a（1+x）2

归纳：如果某个量原来的值为a，每次增长率为x，则增长（降低）1 次后的值为 b1，a（1±x）=b1，增长（降低）2 次后的值为 b2，a（1±x）2=b2，增长（降低）3 次后的值为 b3，a（1±x）3=b3，增长（降低）n次后的值为 b，a（1±x）n=b，如果某个量原来的值为 a，每次增长率为 x，增长 n 次后的值为 b，则 a（1±x）n=b，其中 a代表基数，x代表百分率，n代表变化次数，b代表连续变化结果。

四、恰当运用现代教育技术

快速发展的现代信息化技术，为我们的数学教学提供了很多方便，也有很多应用软件为我们的数学教学提供了方便的平台。但是每一种技术都有它的优缺点，如何更好地利用它的优点，扬长避短，我们必须对它有很深入的了解，能在PPT、白板、微课等软件之间运用自如来回切换，选择适合学生的、适合教学内容的，让它们为我所用，更大地发挥时间、空间的作用，提高学生对整堂课的关注度，并能把这种关注持续到课堂之后。