浅谈完全平方公式的推导、推广及在计算中的应用
李小军
(灌云县九年制实验学校,江苏 灌云)
完全平方公式是初中阶段数学学习的一个重要知识点,也是一个难点。对于公式的内容,大多数学生都能记得,但对于公式的由来、结构特点以及深层次的推广应用还是比较陌生的。因此,在实际运用过程中难免会出现一些差错。下面,笔者就结合自己的教学实践和体会来谈谈对完全平方公式的理解与认识,希望能给大家带来一点启发与帮助。
一、完全平方公式的推导
完全平方公式的内容是:(a+b)2=a2+2ab+b2或(a-b)2=a2-2ab+b2,在教学时,相信老师们也给学生传授了类似于“首平方,尾平方,首尾乘积2倍在中央”的记忆方法或口诀,因此对于公式的内容大多数学生还是能够掌握的,但是这个公式是如何得到的呢?我们老师在教学时都引导学生去探索了,但学生功利得只记住了内容,而忽略了方法。作为学生求知路上的组织者、引导者,老师不光要让学生知道“是这样”,更要让学生知道“为什么是这样”,即“知其然,还要知其所以然”。下面笔者从两个方面来谈谈完全平方公式的由来。
(一)利用多项式乘多项式法则推导
(a+b)2,根据乘方的定义可知:(a+b)2=(a+b)(a+b),然后再根据多项式乘多项式的法则,拿前面括号里的每一项与后面括号里的每一项分别相乘,再把所得的积相加即可。过程如下:
(a+b)2=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
同样,(a-b)2也可以通过以下过程得到:
(a-b)2=(a-b)(a-b)
=a2-ab-ab+b2
=a2-2ab+b2
注意:对于中间到底是“+2ab”还是“-2ab”,这并不是只取决于中间的是“+”号、“-”号,而取决于括号内的“首项”和“尾项”前的符号。首尾同号则加,首尾异号则减。例如:第一个式子中,括号内首项是“+a”,尾项是“+b”,所以中间是“+2ab”;而第二个式子中,括号内首项是“+a”,尾项是“-b”,所以中间是“-2ab”。
(二)利用计算图形面积推导
用不同的方法计算图1最大正方形的面积,图2的阴影面积可以推导出完全平方公式。
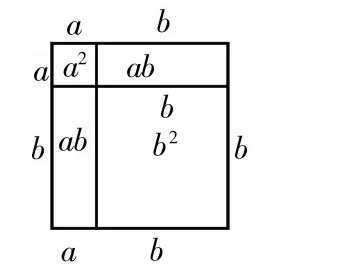
图1
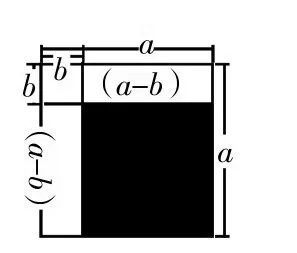
图2
在图1中,求最大的正方形的面积:
方法 1:S大正方形=(a+b)(a+b)=(a+b)2
方法 2:S大正方形=a2+ab+ab+b2=a2+2ab+b2
因为计算的是同一个图形的面积,所以,(a+b)2=a2+2ab+b2
在图2中,求阴影部分正方形的面积:
方法 1:S阴影=(a-b)(a-b)=(a-b)2
方法 2:S阴影=a2-ab-ab+b2=a2-2ab+b2
因为计算的是同一个图形的面积,所以,(a-b)2=a2-2ab+b2
二、完全平方公式的推广
在上文中,我们完成了对(a+b)2=a2+2ab+b2和(a-b)2=a2-2ab+b2的推导,得出了上述完全平方公式。公式中的“a”和“b”,它们只是两个符号,“a”和“b”可能表示一个数,也可能表示一个单项式,也可能表示一个多项式。那么,(多项式)2的计算公式又是什么呢?
我们可以根据乘方的定义和多项式乘多项式法则作如下探索:
(a+b+c)2=(a+b+c)(a+b+c)
=a2+ab+ac+ab+b2+bc+ac+bc+c2
=a2+b2+c2+2ab+2ac+2bc
(a+b+c+d)2=(a+b+c+d)(a+b+c+d)
=a2+ab+ac+ad+ab+b2+bc+bd+ac+bc+c2+cd+ad+bd+cd+d2
=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd
观察上述两式计算过程及结果,我们发现:(多项式)2的计算结果就等于每一项的平方再加上括号内所有项两两相乘的积2倍的和。
三、完全平方公式及推广公式的应用
学以致用,下面结合具体实例来探讨公式的应用。
例 1.计算(a+3)2
分析:此题括号内多项式由两项组成,首项是“a”,尾项是“+3”,可根据“首平方,尾平方,首尾乘积2倍在中央”完成计算。
解:(a+3)2=a2+2·a·3+32=a2+6a+9
例 2.计算(3a-4b)2
分析:此题括号内多项式由两项组成,首项是“3a”,尾项是“-4b”,可根据“首平方,尾平方,首尾乘积2倍在中央”完成计算。
解:(3a-4b)2=(3a)2+2·3a·(-4b)+(-4b)2=9a2+(-24ab)+16b2=9a2-24ab+16b2
综上所述,只要是(多项式)2的形式,都可以用完全平方公式及其推广公式进行简便计算。但在运用过程中,一定要弄清公式结构特征,然后套用规定格式,最后再化简合并,才能顺利达成运用完全平方公式进行简便计算的初衷。

