单值中智信息熵及其多属性决策方法
朱 轮,杨 波
1.常州大学 信息科学与工程学院,江苏 常州 213016
2.常州大学 怀德学院,江苏 靖江 214513
1 引言
数据客户所需要的并不仅仅只是一个存储他们大数据的硬盘,就目前这个阶段而言,数据产品服务商不仅提供到位的数据迁移和存储服务,而且能够在此基础之上提供咨询服务,因此数据产品服务商选择问题是一个重要的研究课题,其本质是一个多属性决策问题。多属性决策(MADM)问题是指针对不同备选方案对不同属性的属性值进行融合,然后对方案进行比较并遴选出最佳方案[1]。由于现实决策问题客观的复杂性以及决策者主观认知的局限性,决策者倾向于用模糊信息表达方案的评估值。文献[2]在1965年首次提出了模糊集的定义,但是随后学者们发现模糊集存在一定的不足,于是相继提出了区间模糊集[3]、直觉模糊集[4]、区间直觉模糊集[5]、犹豫模糊集[6]、正态模糊集[7]、Type-2 模糊集[8]等等概念。这其中,直觉模糊集得到了学者们的广泛关注和研究。但是其不能有效处理不确定和非一致的决策信息,因此,Smarandache[9]主要从哲学的角度首先引入了中智集的概念,然后Wang等[10]结合实际给出了单值中智集的定义。
信息熵是描述信息不确定程度的有力工具,Zadeh[11]最先引入了模糊熵的概念用以衡量决策信息的模糊性。Luca和Termini[12]将模糊熵进行了拓展,给出了更为正式模糊熵定义。基于直觉模糊基数,Szmidt和Kacprzyk[13]提出了直觉模糊熵测度的公理化条件。Ye[14]构建熵加权模型用以计算熵权重。文献[15]提出了区间直觉模糊连续加权熵。李香英[16]首次引入区间犹豫模糊熵的公理性定义。
综上国内外研究可知,熵是模糊集理论中的重要研究课题[17]。因此,Majumdar和Samanta[18]提出了单值中智熵的定义,然而在某些情况下存在一定的缺陷(详见例1)。因此,研究一种合理的单值中智熵概念,并构建简单有效的单值中智熵公式具有较好的实际意义。本文首先引入单值中智熵的公理化定义,同时基于三角函数设计一种信息熵测度公式,最后构建新的单值中智决策方法。
2 基础知识
本章主要介绍一些单值中智集的基本概念,并举例说明现有单值中智熵定义存在的不足。
定义1[10]令X为给定的集合,定义在集合X上的单值中智集 A={<x,TA(x),IA(x),FA(x)>|x∈X}由隶属函数TA(x)、不确定函数IA(x)以及非隶属函数FA(x)表示,其中TA(x),IA(x),FA(x)∈[0,1],且TA(x)+IA(x)+FA(x)∈[0,3]。
为了下文讨论的方便,记α=<Tα,Iα,Fα>≜<α1,α2,α3>为一个单值中智数(Single-Valued Neutrosophic Value,SVNV)。令Ω~是X上所有的SVNV的集合。
定义2[10]令 α=<α1,α2,α3>为一个单值中智数,那么它的补为 αc=<1-α1,1-α2,1-α3>,即 αct,=1-αt,t=1,2,3。
对于一个单值中智数 α=<α1,α2,α3>,Majumdar和Samanta[18]给出了如下单值中智熵的公理化定义。
定义3[18]令 α=<α1,α2,α3>是一个单值中智数,则称函数ε:Ω~→[0,1],如果其满足如下条件:
(1)当 α 是一个精确数时,有 ε(α)=0。
(2)当 <α1,α2,α3>=<0.5,0.5,0.5>,有 ε(α)=1。
(3)ε(α)=ε(αc)。
(4)当 α1+α3≤β1+β3且 |α2-αc2|≤|β2-βc2|时 ,有ε(α)≥ε(β)。
然而在某些情况下,定义3中的条件(4)不一定合理科学,这在例1中可以说明。
例1两个单值中智数分别为α=<1,0,0>和β=<0.5,0,0.6>,那么它们的补分别为αc=<0,1,1>和 βc=<0.5,1,0.4>。因为α1+α3=1+0=1<1.1=0.5+0.6=β1+β3且|α2-αc2|=1=|β2-βc2|,那么根据定义3中的条件(4),可得ε(α)≥ε(β),即 α 的数据信息比 β 更为不确定。然而,显而易见α=<1,0,0>是一个精确数,因此有 ε(α)=0,于是单值中智数α的数据信息应该比β更为精确。因此,从以上分析可知,在某些情况下定义3不一定合理可靠,需要进行改进提升。
3 单值中智信息熵
首先引入了新的单值中智信息熵的公理化定义,然后构建一种对单值中智数进行信息度量的测度公式,并证明其是单值中智熵。
定义4 令 α=<α1,α2,α3>是一个单值中智数,则称函数E:Ω~→[0,1],如果其满足如下4个公理化条件:
(E1) E(α)=0⇔αt=0或αt=1,t=1,2,3。
(E2) E(α)=1⇔<α1,α2,α3>=<0.5,0.5,0.5>。
(E3) E(α)=E(αc)。
(E4)如果β比α更为不确定,即对于∀t=1,2,3,当 βt-βct≤0 时,有 αt≤βt;或者当 βt-βct≥0时,有αt≥βt,那么 E(α)≤E(β)。
对于单值中智数 α=<α1,α2,α3>,运用三角函数构建如下信息测度公式:

定理1 令 α=<α1,α2,α3>是一个单值中智数,那么公式(1)中构建的函数E1(α)满足定义4中的4个公理化条件。
证明 首先构建如下函数:

那么函数 f(x)的导数为:

当 x∈[0,1]时,有 f′(x)≥0;当 x∈[1,2]时,有 f′(x)≤0。因此,当 x∈[0,1]时,函数 f(x)为单调递增函数;当x∈[1,2]时,函数 f(x)为单调递减函数,于是函数 f(x)在x=1处可以取得最大值。从而通过上述分析可知,0≤f(x)≤1,且有 fmin(x)=0当且仅当 x=0或 x=2,fmax(x)=1当且仅当x=1。接下来,将一一证明E1(α)满足定义4中的4个条件。
(E1)假设 E1(α)=0。因为 0≤αt≤1,t=1,2,3,所以αt-αct+1=αt-(1-αt)+1=2αt∈[0,2],t=1,2,3。因此,结合上述分析可知,E1(α)中的每一项均为非负数,于是E1(α)=0 当且仅当 E1(α)中的每一项都为 0,即对于t=1,2,3,有:

根据上述函数分析过程可得公式(4)成立当且仅当αt-+1=0或αt-+1=2,t=1,2,3,即αt=0或αt=1,t=1,2,3。
另一方面,当 αt=0或 αt=1,t=1,2,3时,可得αt-+1=0或 αt-+1=2,t=1,2,3,代入公式(1)易知 E(α)=0 。
(E2)当<α1,α2,α3>=<0.5,0.5,0.5>时,有:
αt-+1=1,t=1,2,3
因此代入公式(1)可得 E1(α)=1。
假设 E1(α)=1。由于 αt-+1∈[0,2],t=1,2,3,所以 0≤E1(α)≤1,那么当 E1(α)=1时,意味着其中的每一项的大小都为1,即对于t=1,2,3,有:

结合函数分析可得,αt-+1=1,t=1,2,3,从而有<α1,α2,α3>=<0.5,0.5,0.5>。

(E4)若对于∀t=1,2,3,当βt-≤0时,有αt≤βt,那么 βt≤=1-βt,t=1,2,3,于是得到:

而 αt-+1=2αt,βt-+1=2βt,所以:

又因为函数 f(x)在x∈[0,1]时为单调递增函数,因此有:
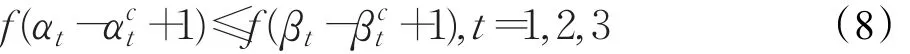
所以 E1(α)≤E1(β)。
类似的,当 βt-≥0 时,有 αt≥βt,可以证明E(α)≤E(β)。综上,结论成立。
根据定理1,有以下定义:
定义5 令 α=<α1,α2,α3>是一个单值中智数,则称公式(1)中构建的函数E1(α)为单值中智熵。
4 单值中智多属性决策方法
现考虑单值中智信息多属性决策问题。假设X={X1,X2,…, }
Xm为一个备选方案集,C={C1,C2,…,Cn}为一个属性指标集合。令w=(w1,w2,…,wn)T是属性集合对
接下来,运用本文提出的单值中智熵公式,建立单值中智多属性决策方法。
步骤1标准化决策矩阵。
若Cj(j=1,2,…,n)均为效益型属性,则决策矩阵不变;否则,对D=(αij)m×n进行如下标准化处理,得到标准的单值中智决策矩阵 D~=(α~ij)m×n:步骤2计算属性权重。

为了尽可能地使决策更为合理准确,决策者一般希望决策过程尽可能地依赖于确定性信息。因此,各属性的权重设定应该尽可能减少不确定信息对决策结果的影响。于是,基于如上思想可建立如下最优化模型:
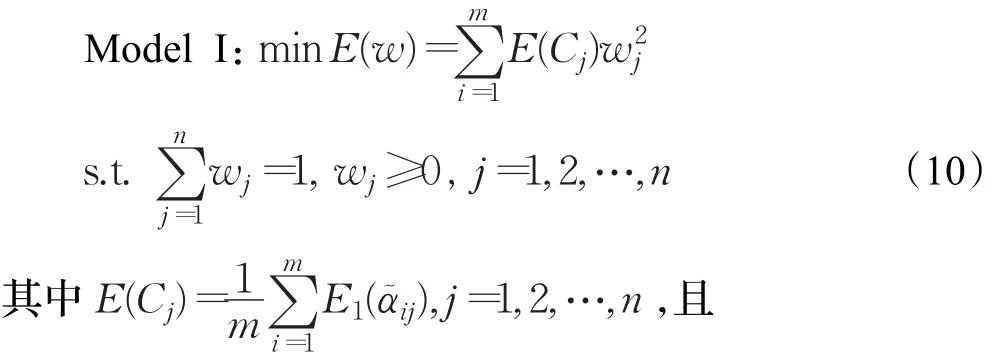


根据Lagrange乘数法计算上述最优化模型Model I,可得属性权重为:步骤3计算备选方案与正负理想点间的距离。首先设计如下正负理想点:正理想点X+={α…,}和负理想点 X-={α,…,,其中=<1,0,0>,=<0,1,1>,j=1,2,…,n。然后计算备选方案 Xi分别与正理想点X+和负理想点X-的距离如下:
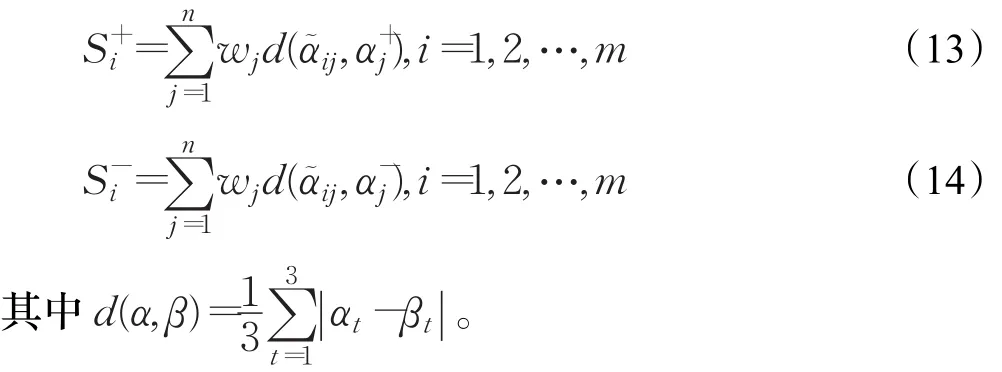
步骤4计算备选方案Xi的贴近度。

步骤5备选方案优劣排序。
根据贴近度Ti(i=1,2,…,m)的大小关系对备选方案进行优劣排序,并选择综合性能最高的方案。
5 实例分析
考虑评估第三方数据产品服务商的选择问题。现有5个备选数据产品服务商为{X1,X2,X3,X4,X5},在优选数据产品服务商时,考虑如下4个评估指标分别为:产品质量(C1)、处理能力(C2)、购买成本(C3)、售后服务(C4),其中C3为成本型指标,其他指标为效益型指标,并且4个评估指标的属性权重信息完全未知。现专家将数据产品服务商在各个属性下进行评估,并将评估值运用单值中智数αij=<>进行表达,从而构建单值中智决策矩阵 D=(αij)5×4。

步骤1由于C3为成本型指标,因此按照转化公式(9)计算得到标准单值中智决策矩阵 D~=(α~ij)5×4如下:

步骤2运用公式(10)~(12)计算属性权重为:
w1=0.192 3,w2=0.320 8
w3=0.126 0,w4=0.360 9
步骤3根据公式(13)和(14)求得所有备选数据产品服务商与正负理想点间的距离如下:

步骤4通过公式(15),计算贴近度:
T1=0.410 8,T2=0.507 4,T3=0.649 7,
T4=0.566 5,T5=0.468 3
步骤5 因为 T3>T4>T2>T5>T1,所以备选数据产品服务商排序结果为X3≻X4≻X2≻X5≻X1。所以综合表现最好数据产品服务商的是X3。
为了体现本文方法的优良性能,与文献[19]中的方法进行对比分析。运用文献[19]中方法处理上述数据产品服务商选择问题的大致过程如下:
首先基于标准化的单值中智决策矩阵D~=(α~ij)5×4,利用文献[19]中的相似度公式:
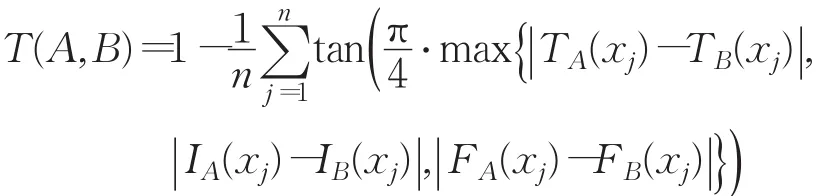
计算各个数据产品服务商与理想点间的相似度:
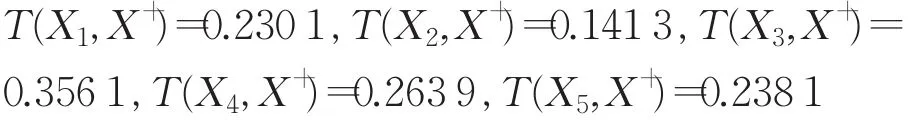
由于 T(X3,X+)>T(X4,X+)>T(X1,X+)>T(X5,X+)>T(X2,X+),所以5个备选数据产品服务商排序结果为X3≻X4≻X1≻X5≻X2,且综合表现最好数据产品服务商的是X3。
通过上面的决策结果可知,虽然运用本文方法和文献[19]中的方法得到的最优结果相同,但是5个备选数据产品服务商排序存在一定的差异。事实上,根据原始的标准单值中智决策矩阵 D~=(α~ij)5×4可知,有 α~21<α~11,α~22>α~12, α~23>α~13, α~24>α~14且 α~21<α~51, α~22>α~52, α~23>α~53,α~24>α~54,这表明数据产品服务商X2的综合性能要优于数据产品服务商X1和X5,这与本文方法得到的排序结果相一致,因此本文方法更为合理可靠。
6 结束语
本文针对现有单值中智熵定义存在一定的缺陷,提出了单值中智熵的公理性定义,构建了一个单值中智信息熵计算公式,并将其应用于单值中智多属性决策模型的建立过程中,最后通过实例验证说明了本文提出方法的可行性和有效性。该方法不仅为单值中智多属性决策问题提供了一种新的解决思路,同时可将方法应用在模式识别、医疗诊断等相关决策问题中。

