基于复杂网络的全球海运网络脆弱性分析
吴 姗,韩晓龙,刘婵娟,胡志华
上海海事大学 物流科学与工程研究院,上海 200135
1 引言
海运网络是由港口、海峡等节点和航线组成的复杂网络,港口工人罢工、海盗、海上交通事故、自然灾害等的扰动都会造成海运网络节点失效。一个或多个节点失效会造成海运网络通达能力下降,影响国际贸易往来。因此,对全球海运网络脆弱性进行分析具有重要意义,有助于科学合理的制定海上运输安全保障机制,且有助于航运企业有针对性的采取预防措施、制定适当的合作机制等。近年来,很多学者倾向于对航空、公路、铁路等交通网络以及电网的脆弱性和鲁棒性进行分析及优化,但对海运网络脆弱性的研究还不多。
脆弱性的概念最早是由Timmerman[1]提出的,脆弱性是一种度,即系统在灾害事件发生时对系统产生不利影响的程度。Berdica[2]最早将脆弱性概念引入道路交通网络中,认为脆弱性是由于不同原因导致可达性下降的特性,将脆弱性定义为交通系统对于异常事件的易受影响性。对于路网脆弱性的研究,Husdal[3]研究脆弱性聚焦于路段或整个网络在各种非正常状况下无法运转的特性。Woolleymeza等[4]研究世界海运网络和航空网络具有类似的拓扑结构特性,在面对故障和攻击时表现出了相似的鲁棒性和脆弱性。Crucitti等[5]在交通网络中,采取有选择删除(蓄意攻击)网络的部分节点或者边时对网络连通性的影响程度。田炜等[6]等对马士基航运的海运网络进行了实证分析,认为世界海运网络局部节点间最短路径过大,大部分节点具有较大的聚集系数等特征。牟向伟和陈燕[7]利用复杂网络理论对班轮航运网络的拓扑特征进行了统计分析。姚红光和朱丽萍[8]以最大连通子图的相对大小作为基本指标来度量航空网络的鲁棒性。王杰和李雪[9]以复杂网络理论为基础,分析了海运网络的拓扑结构,验证了海运网络具有小世界和无标度网络特征。黄常海[10]基于复杂网络理论研究了内河航道网络的脆弱性。王诺[11]研究了网络压力测试方法,探究全球集装箱海运网络脆弱性的变化趋势。张广胜等[12]分析物流服务供应链网络节点作用规律,引入聚集系数、最大连通度及连通效率作为网络脆弱性测度指标,基于所构建攻击策略对二级物流服务供应链网络进行实例研究。程光权[13]等提出一种基于节点状态演化级联失效模型的节点重要度评估和网络脆弱性分析方法。
由以上分析可知,国内外学者对于交通网络脆弱性的研究主要集中于航空运输网络和公路网络,对于海运网络的研究鲜少,且已有研究大多只是分析海运网络拓扑结构,而并未对全球海运网络脆弱性进行分析。本文基于复杂网络理论和方法,在全球海运网络拓扑结构的基础上从全局角度对全球海运网络脆弱性进行分析,并用MATLAB分析港口度、平均聚集系数、网络平均距离等指标,最后定量计算各个港口的脆弱性,同时比较全球集装箱海运网络在面对不同方式下的攻击时的海运网络脆弱性变化。从局部到整体对海运网络进行脆弱性研究,为日后对海运网络优化和对航线或港口由某种原因短暂性失效提供理论解决依据。
2 数据采集
以往研究多采用马士基集团下的航运数据进行实证分析,为了统计数据的完整性,力求构建最能反映真实情况的海运网络,本文以世界前10大班轮公司中7家公司的航运数据为研究基础。这7家公司所占全球海运运输市场份额合计达45.6%,如表1所示。虽然市场份额不大,但总的服务网络已遍布世界6大洲,涉及全球最基本的海运港口,所以该航运数据基本可以代表目前全球国际航运状况。以各船公司(马士基、达飞、赫伯罗特、长荣、中远、中海和韩进)网站的船期表为基础,分别跟踪和获取每条航线上一个航期中班轮挂靠的所有港口,跟踪时间为2015年10月到2016年1月。经过港口名称规范化后,统计得港口总数为777个,所涉及的航线总数为7 553条。
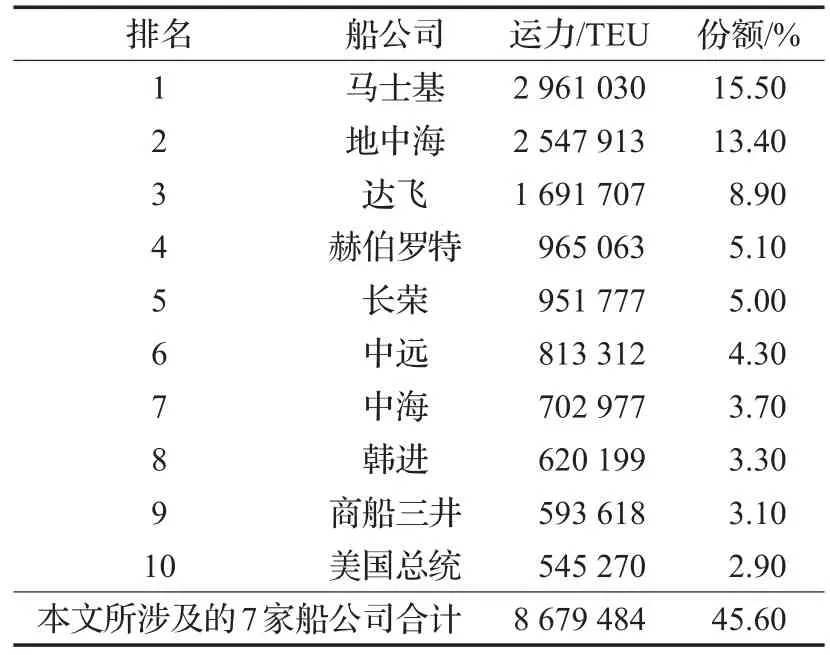
表1 7家主要航运公司TEU及市场份额
为便于理论分析,将全球集装箱海运网络中的各个港口抽象为网络中的各个节点,港口之间航线抽象为边,构建一个简单的无向无权网络。以V={ }1,2,…,N表示港口的集合,N表示港口总数。Ri,j表示港口i和港口 j之间是否存在班轮航线。若i和 j之间存在边的连接,则Ri,j≠∅ 且Ri,j⊆R;若i和 j之间尚未建立连接,则Ri,j=∅。其矩阵表达式为:
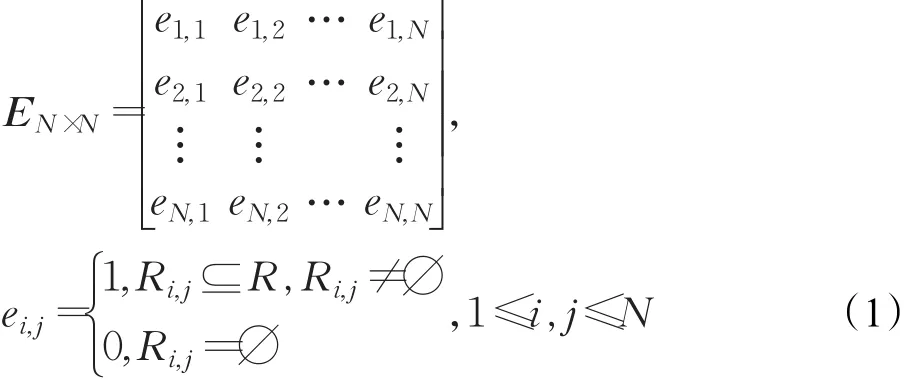
式(1)中eij=0或eij=1分别表示港口i和港口 j之间不存在或存在边的连接,据此得到一个777×777的0-1矩阵。
应用UCINET软件绘制全球集装箱海运网络拓扑结构图,为增强显示效果,本文选择港口节点连边数前100位(度值前100位)港口进行了显示,如图1所示。
3 海运网络拓扑结构参数统计
3.1 度与度分布
在复杂网络中,度是节点的重要特性之一,某一节点i的度k是指与该节点相连接的节点的数目。在海运网络中,度值较大的节点则表明有较多的航线经过该港口。
港口i的度是指与此港口连接的其他港口数目,用N(k)表示;网络中港口的度分布概率用度分布函数P(k)表示,其含义是随机选择一个节点恰好连接k条边的概率。其中,N为港口总数,P(k)为度是N(k)的节点数占网络节点总个数的比例。计算公式:


图1 度值前100港口集装箱海运网络拓扑结构图
根据节点度分布函数P()k以及全球777个港口的航线数据,得出全球集装箱海运网络各节点度值及度分布分别见图2、图3。其中,网络中节点度值最大为138,平均度值为=9.720 7,说明在全球集装箱海运网络中经过任一港口的航线数平均约为10条。

图2 海运网络各节点度值
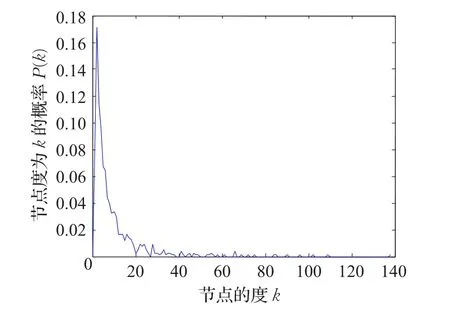
图3 海运网络各节点度分布
3.2 网络聚集系数
在海运网络中,聚集系数的分布反映航线的密集程度,其中网络聚集系数对海运网络脆弱性的影响呈负相关,聚集系数越大,该网络对其节点产生的影响越大。节点的网聚集系数是计算网络中描述中各港口的聚集情况,即网络的紧密程度,设C为网络聚集系数,有:

式中,E(i)表示节点i的邻居节点之间实际的连接边数,T(i)表示节点i的k个邻居节点之间可能形成的最大连接数,设节点i的度为k,易知,T(i)=k(k -1)2。因为N为港口总数,所以整个网络中所有节点的平均聚集系数c(s),有:

其中0≤c(s)≤1,当c(s)=0时,表示所有节点都是孤立节点,没有边连接;当c(s)=1时,表示网络成为两两节点之间完全的边连接。根据公式(4)以及全球777个港口的航线数据,计算得出整个网络平均聚集系数为c(s)=0.484 4,说明全球航线的分布较为密集。
3.3 网络平均距离
网络的平均最短路径L是指网络中所有节点对间的最短路径的平均数。一般货物运输过程中停靠的港口数越少越好,这样既可以节省时间,也能保证货物质量安全。在无向无权网络中,任意两个节点i和 j之间的距离dij被定义为这两个节点的最短路径所包含的边数。网络的平均最短路径L是指网络中所有节点对间的最短路径的平均数,如公式(5)所示。其中N为网络节点总数。

通过以上计算、分析可以看出全球海运网络的节点度分布基本满足截断递减幂律分布,度值大的节点所占比重较小,而度值小的节点占比重较大。全球集装箱海运网络中网络平均距离分布曲线见图4。
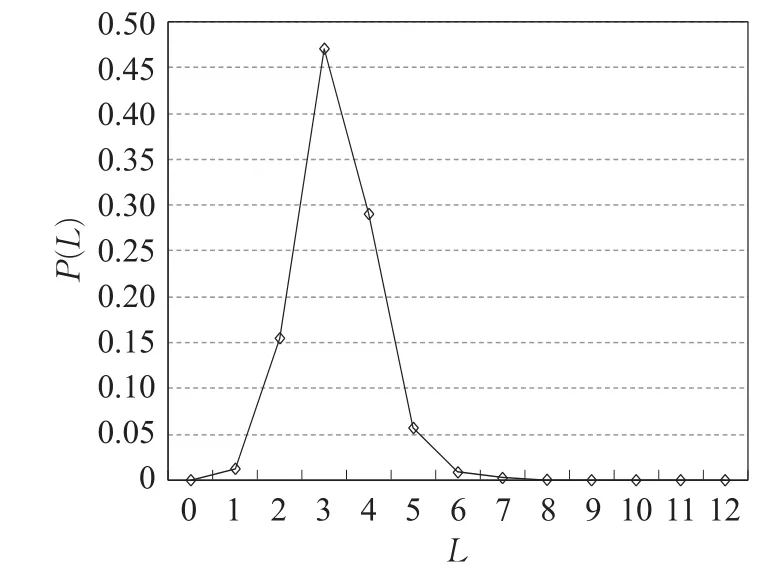
图4 全球集装箱海运网络中平均最短路径分布
根据图4可知,集装箱海运网络中网络平均距离近似服从正态分布,大多数节点对之间的网络平均距离集中在2~5之间,说明在全球集装箱海运网络中,将一票货物从一个港口送达至另一港口平均所需停靠的港口数量约为3或4个。
4 全球集装箱海运网络脆弱性分析
4.1 基于节点脆弱度的关键节点识别
依靠网络拓扑参数指标能够判定一些重要节点,如根据度值大小,聚集系数等。但是,仅仅依靠拓扑指标来判定节点在网络中的重要性是不全面的。因此,本文中提出节点脆弱度的概念来识别全球集装箱海运网络中的关键港口。
根据文献[14-15]对网络效率的定义:节点i和节点j之间的网络效率用eij表示,eij可以看做是节点i和节点 j之间最短路径长度dij的倒数,如式(6)所示。如果节点i和节点 j之间无连接存在,那么eij为0。整个网络的效率可以表示为式(7)。记原始网络的网络效率为E,某个节点失效后的网络效率为Er,那么某节点r的结构脆弱度如式(8)所示。根据公式(7)求得原始海运网络拓扑结构的网络效率为0.332 8。
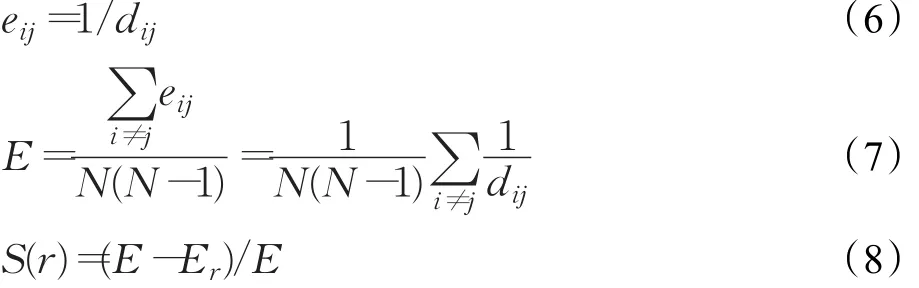
运用MATLAB编程求解各节点脆弱度,编程对数据进行处理,可得出不同节点失效后各节点的脆弱度,表2是脆弱度前60的节点排名。
由表2可以看出,舟山港的脆弱度最大,为0.332 9,其次为泽布吕赫(比利时西部的一个港口)、中山港、张家港、漳州港、湛江港、乍浦港(嘉兴港)、肇庆港、镇江港、日本四日市港。舟山港的结构脆弱度最大的主要原因是,舟山港是一个以水运中转为主要功能的深水良港,与宁波港合并后,资源得到了整合,在整个海运网络中直接相连的航线数量增多,充当了更多港口对的中介作用,这一港口失效后,会严重影响网络的结构性能,甚至造成网络瘫痪,这也体现了舟山港在整个海运网络中的重要性和枢纽地位。货物吞吐量较大的上海港、新加坡港、鹿特丹港、黑德兰港等在世界集装箱海运网络中的脆弱度并不大。因此,不能仅仅根据港口货物吞吐量来判定一个港口在全球海运网络中的重要性。
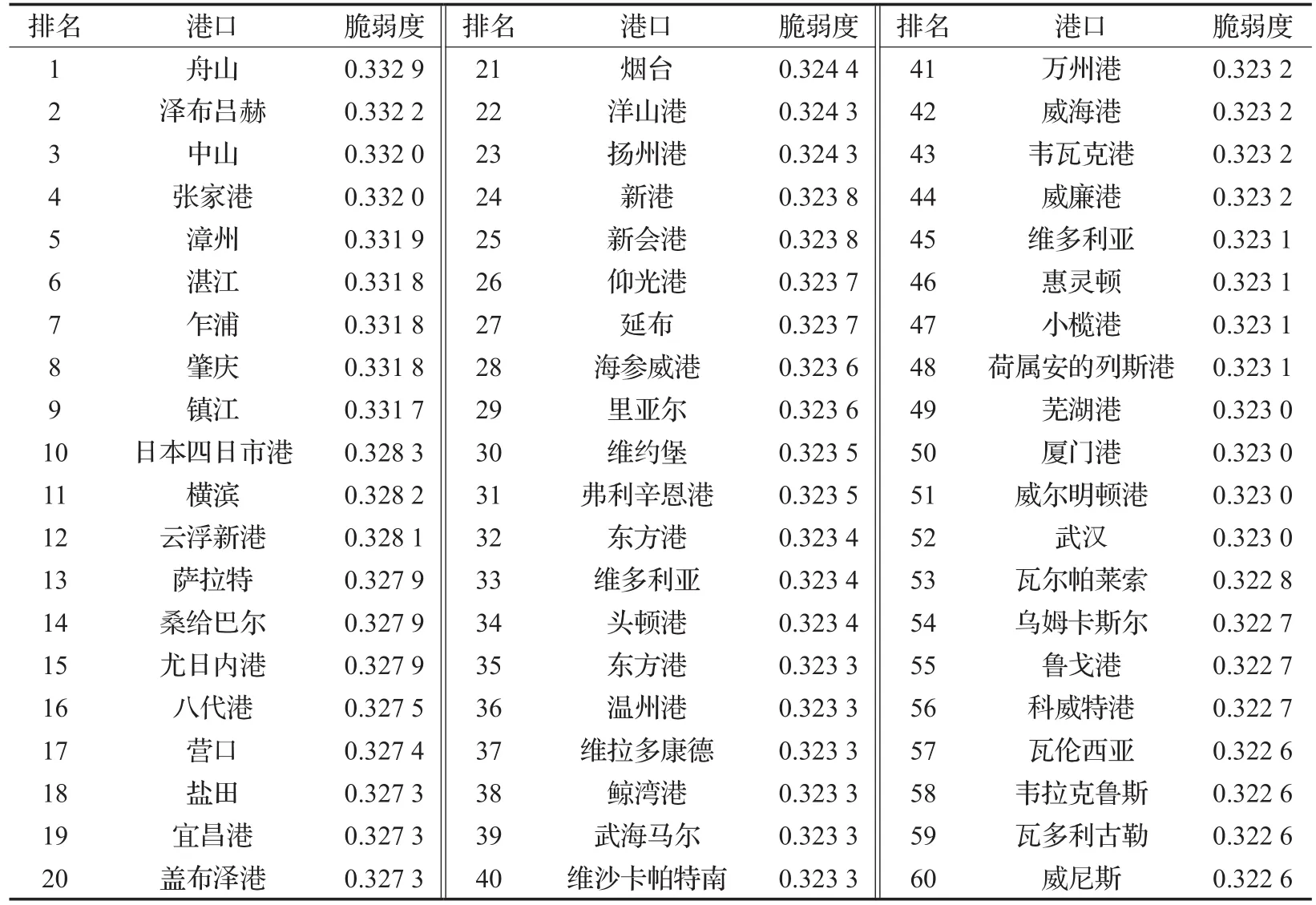
表2 港口脆弱度计算结果(前60)
4.2 全球集装箱海运网络全局脆弱性分析
全局脆弱性是从整体的角度分析网络的脆弱性,了解整个海运网络在内部或外部的某些诱因下而引起的网络连通性的变化。这些诱因包括:海运网络拓扑结构的不合理、自然灾害、海盗及海上恐怖主义、政治因素、海上交通事故等多种因素。为了区分攻击方式的不同对港口脆弱性分析的不同影响,这里把攻击模式分为随机攻击和蓄意攻击两种。
在随机攻击模式下,海运网络中的各个节点具有相同的被攻击概率,每次随机攻击网络中的某个节点以及与之相连的边,并计算节点移除后网络效率等性能指标的变化情况。随机攻击主要测试随机事件对海运网络中航线通达能力的影响。
在蓄意攻击模式下,按照节点脆弱度的大小对所有节点进行排序,最先移除具有最大脆弱度的节点,如果网络中有多个节点具有相同的脆弱度,随机移除其中一个节点即可,移除网络中节点脆弱度最大的节点后,计算网络中各项性能指标,然后重新移除网络中节点脆弱度最大的节点,重复进行下去直到达到预设条件。
本文应用MATLAB软件,设计对全球集装箱海运网络进行随机攻击和蓄意攻击两种攻击策略,计算受到攻击后的网络效率。全局脆弱性分析计算具体步骤归纳如下:
步骤1利用初始网络拓扑结构,求出关键的节点指标P(k)、c(s)和L。
步骤2按照不同攻击模式的删除策略选取被攻击的节点,移除网络中的相应节点。
步骤3根据新的网络拓扑结构,计算出网络效率E和脆弱度S(r)。
步骤4判断是否符合预设条件,若结果不符合条件,返回步骤2,反之,算法结束。
按上述步骤,计算得出在不同攻击模式下,随着攻击节点数的增加,网络效率的变化情况。随机攻击和蓄意攻击下网络效率计算结果见表3,网络效率走势图见图5。
根据图中曲线走向可以得知,在蓄意攻击下指标下降速度更快,随着被攻击节点数量的增加,指标下降速度逐渐变快。蓄意攻击比随机攻击对网络的破坏程度大,这是因为蓄意攻击模式下每次删除网络中脆弱度最大的节点,这些节点对海运网络的连通性和稳定性起着非常重要的作用,攻击这些节点会使网络的拓扑结构发生剧烈的变化,从而使网络的网络效率迅速减小。全球集装箱海运网络在面对蓄意攻击时表现出较大的脆弱性,因此应该重点关注蓄意攻击可能引发的网络脆弱性,对脆弱度较高的港口加强预防,切实保障这类港口的正常高效运行。

表3 两种不同攻击方式下网络效率变化表
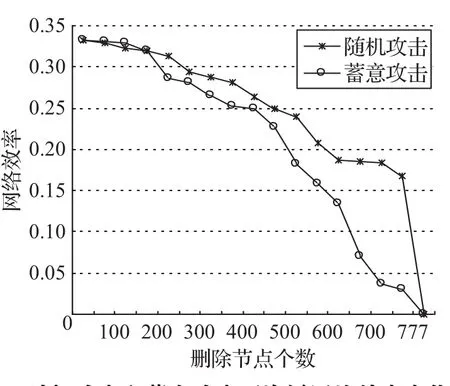
图5 随机攻击和蓄意攻击下海运网络效率变化图
为提升各节点的弹性,脆弱度较高的港口可以选择与邻近的脆弱度稍低的港口进行合作,当脆弱度较高的港口因不可抗力造成中断时,合作港口可以及时响应,协助处理受攻击港口在中断期间的业务。此外,脆弱度较高的港口也可以协助邻近的脆弱度稍低的港口进行业务水平的拓展,均衡各港口在航运网络中的不可替代性程度,降低其自身的脆弱度。在实际港口分布中,有很多临近的港口形成双、多核协同港,如宁波港、舟山港与上海港,香港港与深圳港,新加坡港与巴生港等。这些相邻的节点类似于计算机备份机制,一旦某一港口在某种情况下部分或全部短暂性失效,这些相邻的协同港口立即承担起航运运输功能,港口间协同合作可以使集装箱海运网络失灵后受到的影响减少。
5 结论
本文基于复杂网络理论和方法,在搜集了2015年最新全球10大班轮公司中7家航运公司数据的基础上构建了全球集装箱海运网络的拓扑结构。首先计算能够揭示拓扑网络结构特性的相应参数;然后提出脆弱度的概念来进行网络中关键节点识别,分析得出舟山港脆弱度最大,为0.332 9,而货物吞吐量较大的上海港、鹿特丹港、新加坡港等的脆弱度并不大,因此,不能仅仅根据港口货物吞吐量来判定一个港口在全球海运网络中的重要性。最后应用MATLAB软件进行仿真实验,从全局脆弱性角度分析海运网络脆弱性。仿真实验结果表明全球集装箱海运网络在面对蓄意攻击时表现出较大的脆弱性,在移除相同节点数时,蓄意攻击的网络效率明显低于随机攻击下的网络效率。因此,为了保障全球海上运输的安全性和可靠性,应该对全球集装箱海运网络中脆弱度较大的舟山港、泽布吕赫中山港、张家港、漳州港、湛江港等加以重点保护。
海运网络脆弱性分析能够为集装箱海运网络的规划、加强重点航线的维护、应急运输备用港口及航线选择等提供理论依据。针对集装箱航线上可能发生的各种突发事件,建立相应的场景,分析脆弱度变化,为重新优化航运线路提供帮助。对于网络脆弱性分析,考虑各个港口和海运航线失效的概率和时间等方面,将是本文后续研究的方向。

