最迟预定时刻差异化背景下的时隙定价策略
付长松,陈淮莉
上海海事大学 物流研究中心,上海 201306
1 引言
在线需求履约(demand fulfillment in E-Business)末端的配送活动分为“客户自提”(customer pick-up)和“送货上门”(home delivery),而“送货上门”又被分为“无人值守”(unattended home delivery)和“有人值守”(attended home delivery)。“有人值守”的配送方式避免了因收货人不在而导致的商品空投或者商品投放在无人看管的信箱等设施后发生货损。为了在“有人值守”方式下方便客户,网络零售商会提供一组货物送达的时间窗供客户选择,国内外专家称此时间窗为配送时隙(delivery time slot)。最早提供配送时隙服务的网络零售商有国外的Peapod、Ocado和Tesco等。早期的网络零售商为了给拣货活动提供足够时间,即使是高度自动化的Peapod都要求客户提前至少10个小时以上预定配送服务,并且所有时隙的最迟预定时刻均是同一个时刻点。随着电商行业的高速发展,配送时隙的预定提前期不断缩短,同时时隙的最迟预定时刻出现差异化。例如国内自建物流的电商企业京东提供“标准达”配送服务,“标准达”服务允许客户在购物当天的23点前预定第二天的两个分别为“09:00—15:00”和“15:00—19:00”的配送时隙,而在购物当天的23点到第二天的11点前的时段内仅能选择第二天的第二个时隙“15:00—19:00”,这两个时隙的最迟预定时刻存在差异。
国内外专家关于配送时隙的研究目标主要放在配送路径设计与优化等技术性内容[1-6],仅有少数研究者基于需求管理思想对时隙收益策略进行研究。Geunes[7]建立了需求量和需求频率对价格敏感情况下的交付定价模型,以客户区域和价格为决策变量优化收益率。Lewis[8]等人和Campbell[9]等人均研究了运费折扣激励的影响。前者从订单利润角度出发,通过某网络零售商的销售数据分析得到折扣激励能提升订单交易率和扩大交易额,同时发现折扣对客户选择行为的影响是非线性的。后者针对网络零售商实时接受订单的动态环境,提出利用运费折扣诱导新到达订单在已接受订单的基础上选择使配送路径更高效的时隙,并验证了其在提升利润上的巨大潜力,但研究是在时隙选择概率与价格的联系是线性的假设下进行的。而后Kurrsad[10]等人在收益管理思想下提出对运能紧张的时段采用动态定价策略,利用马尔可夫决策过程原理以及贝尔曼最优定理建立动态时隙定价模型,分析了得到在动态定价的环境中,剩余运能的减少以及各时隙最迟预定时刻提前均会对使时隙最优价格上涨,但对最迟预定时刻的研究成果仅适用于动态定价环境。陈淮莉[11-14]等人引用效用函数和MNL模型,依次建立考虑订单需求波动、时隙替代行为、时隙宽度以及交付期约束等因素的最大时隙收益价格策略,研究表明时隙效用、订单到达分布以及交付期对时隙的定价起很大的影响,同时得到考虑时隙替代行为后的定价策略能带来更多收益,但这些研究没有考虑时隙运营成本。
本文在以下两个出发点下构建:(1)早期专家们在研究静态的时隙价格策略时,将所有时隙的最迟预定时刻定为同一个时刻点,忽略了最迟预定时刻存在差异化的情况。差异化的最迟预定时刻将单个订单到达周期切割成多个订单到达阶段,时隙的时效性随着订单到达阶段的后移而改变,选择概率也因可选择时隙集合的改变而变化;(2)绝大多数研究者在研究配送时隙价格时都忽略了时隙运营成本。如图1中网络零售商在线订单履约过程所示,配送路径的规划是在订单接受之后进行的,所以包含运输成本在内的实际的时隙运营成本只有在一个订单到达周期截止时才能算出,这导致了绝大多数研究者在研究时隙价格均是以不考虑时隙运营成本的时隙最大收益或者接受订单数最大等为目标进行,忽略了时隙运营成本对价格以及总利润的影响。在分析以上背景后,本文针对单订单到达周期建立最迟预定时刻差异化背景下考虑时隙运营成本的最优时隙价格模型,并进行了分析。丰富了网络零售商在线需求履约中的配送时隙价格研究,为网络零售商日常管理和运营提供有效意见。

图1 网络零售商在线订单履约过程
2 参数
2.1 集合
M为配送时隙集合,i=(1,2,…,m)∈M;
H为预定阶段集合,x=(1,2,…,m)∈H。
2.2 参数
λ为单位时间内到达单位订单的概率;
(ai,bi)为配送时隙i的时间区间,ai为时隙i的起始时刻,bi为时隙i的结束时刻;
Ti为时隙i的预定提前期;
Wi为时隙i的最大配送能力;
α为客户的价格敏感系数;
vi表示时隙i的基础效用;
v0表示不选择时隙直接离开行为的基础效用;
e为时隙单位时间内产生的固定成本;
z为配送区域的面积;
d为本区域的最大半径和最小半径的平均值;
s为单位配送里程的运输成本;
k是个无量纲的常数,与配送区域面积有关。
2.3 变量
Qi为时隙i的预计总订单接收量;
fi为时隙i的固定成本;
oi为时隙i的变动成本;
Ci为时隙i的运营成本;
Lix表示时隙i在订单到达阶段x的可被选择性,等于1时表示可被选择,为0则不可被选择;
Ui为时隙i的综合效用;
U0为不选择时隙的行为的综合效用;
δi为时隙i在某配送区域内接受订单的密度;
DRi时隙i的收益;
Revenue为全部时隙的总收益;
Profit为全部时隙的总利润。
2.4 决策变量
ri为配送时隙i的价格。
3 模型构建
3.1 配送时隙选择概率
效用函数是离散选择概率模型的应用基础,引用效用函数构建考虑价格后的配送时隙综合效用。设vi表示配送时隙i对客户的基础效用,设v0表示不选择时隙直接离开行为的基础效用,客户对时隙价格的敏感系数为α(α>0),当时隙i的价格ri上涨时,时隙i的综合效用会减弱。所以考虑价格后的时隙综合效用以及不选择时隙直接离开行为的综合效用分别由式(1)中Ui和式(2)中U0所示。而式(1)和式(2)中的 εi和 ε0表示随机事件的效用,但在在线购物活动中发生随机事件的可能性微乎其微,所以可以忽略εi和ε0,得到更新后的时隙i的综合效用表达式如式(3)和式(4)所示。

离散选择模型有很多种,例如多项Logit模型、嵌套式Logit模型、Probit模型和混合式Logit模型等。本文研究客户对不同配送时隙的选择问题,各选择的属性与其他类别无关,多项Logit模型(又称MNL模型)最为恰当,利用MNL模型预测客户选择时隙i的概率表示如下:

在收益管理思想中,价格调整是能控制需求分布以使收益达到最大化的经典工具之一。而价格调整对配送时隙的运营管理也有其巨大影响。参见Kurrsad[10]等人对时隙选择概率的研究后得到引理1和引理2。
引理1上调某个配送时隙的价格后,此配送时隙被客户选择的概率会下降。
证明 将配送时隙i被客户选择的概率对其价格ri求导,求导过程以及结果如式(6)所示。因为α和 pi是大于零的正数,并且求导结果等于-αpi(1-pi),则求导结果总是小于0的,因此时隙i被选择的概率 pi与它的价格ri存在消极关系。所以当时隙i的价格上涨时,其被选择的概率下降,i∈M。

引理2上调某个配送时隙的价格后,除此时隙外的其他任意配送时隙被客户选择的概率上升。
证明 将配送时隙d被客户选择的概率对时隙i的价格ri求导,求导过程以及结果如式(7)所示,需满足∀d≠i。因为α、pd和 pi均是大于零的正数,并且求导结果等于αpdpi,则求导结果是大于0的,因此任意配送时隙d被客户选择的概率 pd与时隙i的价格ri存在积极关系。所以当时隙i的价格上涨时,除时隙i外的任意时隙d被客户选择的概率上升,满足∀d≠i。
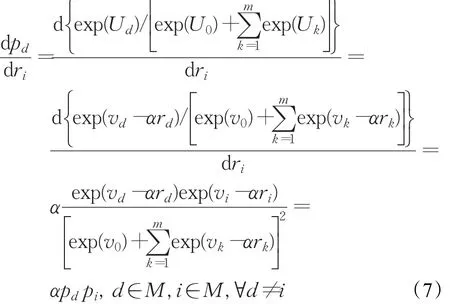
3.2 订单接受量
假设有m个配送时隙,令ai与bi表示时隙i的起始时刻和终止时刻,i∈M。设定Ti为时隙i的预定提前期,该时隙的最迟预定时刻为它的起始时刻向前推移与提前期Ti等长的时间宽度后的时刻点。m个配送时隙的最迟预定时刻将单个订单到达周期分割为m个订单到达阶段,分别为(0,a1-T1),(a1-T1,a2-T2),…,(am-1-Tm-1,am-Tm),见图2。阶段1的起始时刻为0,终止时刻为a1-T1,在阶段1终止时刻前到达的订单可以选择所有配送时隙。同理,在订单到达阶段x内的可选择时隙的集合为不包含最迟预定时刻早于时刻ax-Tx的所有时隙。可见,最迟预定时刻差异化背景下可被选择时隙的集合随着订单到达阶段后移而改变。在阶段x内到达的订单可选择时隙的集合为(x,x+1,x+2,…,m),此时客户在阶段x内选择时隙i的概率如式(8)所示。而把式(8)简化后得到等价的式(9)和式(10),其中Lix等于1时表示在x阶段可选择配送时隙i,等于0时则不可选择。


图2 最迟预定时刻差异化背景下的订单到达阶段

假定订单到达服从泊松分布,设在极其微小的单位时间内到达单位订单的概率为λ。则阶段x内时隙i预期总的订单接受量等于此阶段时长“(ax-Tx)-(ax-1-Tx-1)”与时隙i在此阶段内的单位时间接受单位订单的概率的乘积。是一个联合概率,它等于阶段x内单位时间到达单位订单的概率λ与此阶段内订单选择配送时隙i的概率的乘积。配送时隙i总的订单接受量Qi等于其在各个阶段订单接受量的累加值,见图3和式(13)。Qi需要满足时隙最大运能约束式(14),Wi表示时隙i的最大运能。
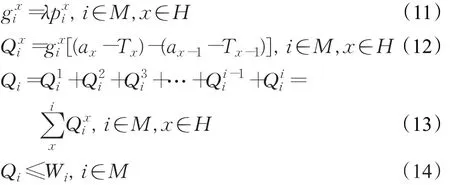

图3 配送时隙i订单接受量
3.3 配送时隙运营成本
配送时隙的运营成本包含固定成分和变动成分,本文将二者分别简称为固定成本和变动成本。固定成本大小与在时隙内为履行配送约定而雇佣的车辆和人员数量以及进行履约活动的时间长度有关。但时隙内配送车辆以及人员的数量是由具体的配送方案优化求解得到的,为方便成本模型构建,这里默认一个时隙仅由一辆车和一个人员服务,此时固定成本仅受需求履约活动的时间长度影响,而配送时隙的宽度对此时间长度有很好的代表性,利用此关系得到配送时隙i的固定成本如式(15)所示,其中e表示配送时隙的单位时间宽度的固定成本均值。变动成本与时隙内的车辆走行里程有关。据Agatz[15]研究,时隙内两个地点的配送距离与配送区域的平均半径有关,关系系数为k/δ,其中k是无量纲的常数,δ表示时隙在该区域内的配送订单密度,它等于时隙内配送的订单量与配送区域面积的商。设δi表示时隙i的配送订单密度δi,d表示本区域的最大半径和最小半径的平均值,结合k/δ、配送区域平均半径与平均配送距离的关系,时隙i内单位订单的平均配送里程dˉi可用式(17)表示。而时隙i内车辆的总走行里程di见式(18)。设s为单位配送里程的运输成本,则时隙i的总变动成本oi见式(19)。时隙i的总运营成本Ci等于变动成本oi加上固定成本 fi,见式(20)。

3.4 最优时隙价格目标函数
客户在选择配送时隙后成功地与网络零售商订立需求履约约定,此时配送时隙总利润等于已接受订单的订单支付的配送费用减去运营成本,所以时隙i带来的总利润DRi如式(21)所示:

设Profit表示所有时隙的总利润,整理前文内容后得到最迟预定时刻差异化背景下考虑时隙运营成本的最优配送时隙价格目标函数如式(22)所示,此时的目标函数是以总利润Profit最大设定的:

4 算例分析
本文采用京东的“标准达”服务为例子构建配送时隙。假设某网络零售商向c地区提供两个配送时隙,分别为第二天的“9:00~15:00”和“15:00~19:00”,这二者的最迟预定时刻分别为前一天的“23:00”和第二天的“11:00”,订单到达周期为前一天的“11:00”到第二天的“11:00”。将上述数据进行单位变换处理,在原来时刻点单位为小时的基础上乘以60变为以分钟为单位的时刻点,以订单到达周期的初始时刻第一天的“11:00”为起始点,令其等于0,然后推定第二天的两个时隙的时间范围变成“1320:00—1680:00”和“1680:00—1920:00”,二者的最迟预定提前期10个小时和4个小时也相应转变为600和240,其他参数见表1。为验证模型有效性,采用Matlab9.1进行模拟计算。计算过程如下:根据案例时隙个数和初始参数信息,将初始模型转化为以时隙价格r1和r2为决策变量的具体的模型。然后令求取最大值的目标函数整体加上负号,使其变为求最小值的目标函数。最后引用能求解非线性多元函数最小值的fmincon函数,根据fmincon的语法格式,将转化后的目标函数和约束条件输入并进行函数最小值求解。
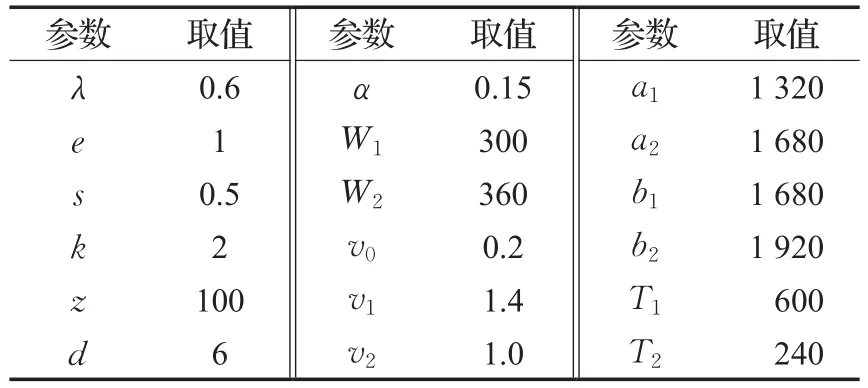
表1 参数
(1)考虑时隙运营成本的必要性
本文在最优时隙价格制定中加入了时隙运营成本考虑,如果要比较考虑时隙运营成本是否有必要,则需要比较二者的总利润。考虑时隙运营成本的最优时隙价格模型是以时隙总利润最大为目标建立的,见3.4节。而不考虑时隙运营成本的最优时隙价格模型是以时隙总收益最大为目标建立的,计算此模型下的总利润需分两步进行。第一步先计算出不考虑时隙运营成本而是以时隙收益最大为目标的最优时隙价格和订单接受量,其目标函数见式(38),满足约束式(20)~式(30)。然后在此基础上根据时隙运营成本公式计算出最终总利润,总利润公式见式(40),满足约束式(31)~式(36)和式(39)。固定其他参数,令订单到达率分别为0.40、0.50、0.60、0.70和0.80,通过计算得到不同订单到达率下的最优时隙价格和总利润如表2所示,表2中括号内的数据是在求最大时隙收益策略得到的,而括号外的数据是在求最大时隙利润策略下得到的。
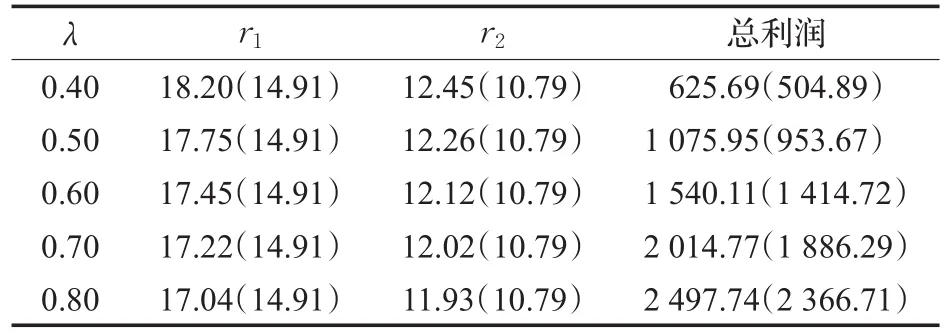
表2 c地区在不同订单到达率下的时隙价格和总利润
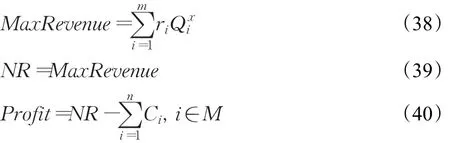
由表2可知,随着订单到达率的上升,考虑运营成本与不考虑运营成本两种时隙定价策略下的总利润均在扩大。但总体上可看出考虑运营成本的时隙定价策略创造的总利润更大,所以在制定最优时隙价格时考虑运营成本是必要的。而从价格上分析时,可看到在时隙运能较充分时,不考虑运营成本的最优时隙价格不随订单到达率上升而扩大,相反地考虑运营成本的最优时隙价格随订单到达率上升而下降。所以在将时隙运营成本纳入时隙定价策略下,当某区域的订单到达率低时需制定较高的时隙价格,相反地在订单到达率高时需制定较低的时隙价格。
(2)配送区域对时隙价格的影响
假定除c地区外还存在a地区、b地区和d地区,a地区、b地区和d地区的面积分别为20、60、140,这三个地区的半径均值分别为3、5和7.5。假设这三个地区获得的时隙服务与c地区一样,a、b、c、d四个地区除了面积和半径均值不同外其余特征均相同。令订单到达率λ分别等于0.10、0.30、0.50、0.70和0.90,模拟面积从小到大的a地区、b地区、c地区和d地区在不同订单到达率下的各项数据,分别见表3~表6。根据表3~表6得到图4。
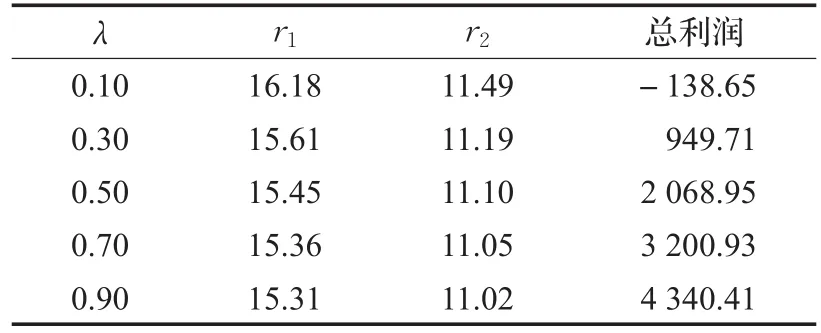
表3 a地区在不同订单到达率下的价格和总利润

表4 b地区在不同订单到达率下的价格和总利润
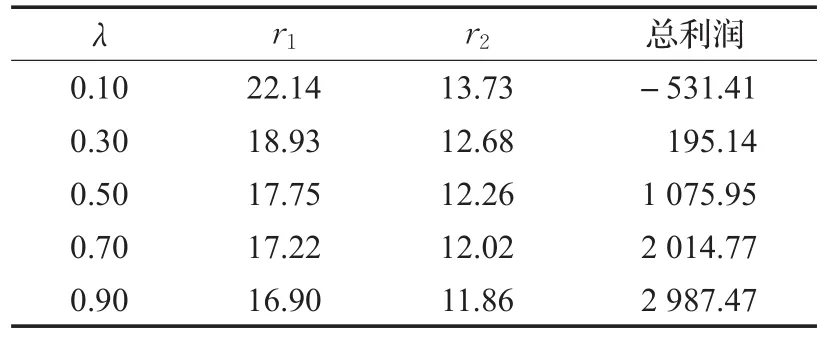
表5 c地区在不同订单到达率下的价格和总利润
从表3~表6可看出,当订单到达率等于0.10时,四地区的时隙价格虽然均是使总利润达到最大的最优价格,但网络零售上的利润仍出现负值,也即是亏损,由此得到网络零售商在对订单到达率非常低的区域应该考虑取消配送时隙服务或者减少时隙数量以避免亏损。而在图4中存在两个特征:第一,无论配送区域面积大小,当订单到达率上升时,时隙的最优价格都会有下降的趋势。但面积最小的a地区的价格下降趋势并不明显,反而是面积最大的d地区的价格下降趋势很大。第二,当四个地区的订单到达率相同时,面积最大的d地区的最优时隙价格最大,而面积最小的a地区的最优时隙价格最小。结合以上两个特征可知道,考虑时隙运营成本的最优时隙价格大小、下降的幅度和该区域的面积、订单到达率之间存在巨大联系。订单到达率小并且面积大的地区的时隙价格应该被制定得较高,并且它对订单到达率的波动很敏感,当订单到达率上升时最优时隙价格会有较大幅度下降。而订单到达率大同时面积小的地区的时隙价格应该被制定得较低,它对订单到达率的波动不敏感,当订单到达率上升时可以令其固定不变。
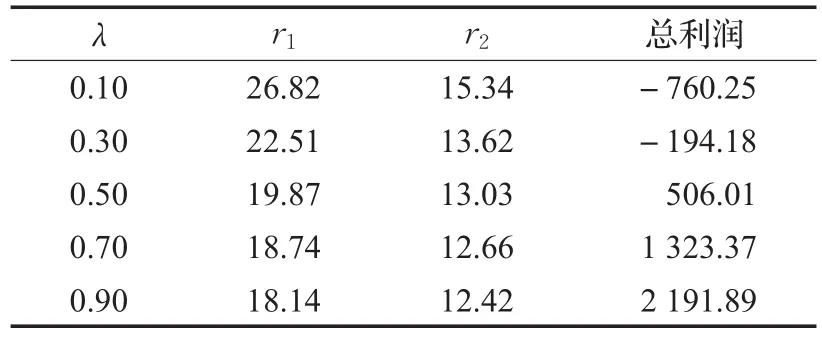
表6 d地区在不同订单到达率下的价格和总利润

图4 不同订单到达率下的四地区时隙价格
(3)不同时隙最迟预定时刻的影响
固定时隙2提前期,单独地令时隙1提前期在原来基础上分别延长120、缩短120和缩短240,则相应地会使时隙1的最迟预定时刻提前120、推迟120和推迟240,此时再考虑上最初的时隙提前期后形成三组不同的最迟预定时刻。然后计算订单到达率λ分别等于0.10、0.30、0.50、0.70和0.90的最优时隙价格、订单接受量和总利润,结果见表7~表10,同时结合表7~表10中的最优时隙价格和总利润值得到图5和图6。

表7 初始最迟预定时刻下的影响

表8 提前时隙1提前预定时刻120的影响
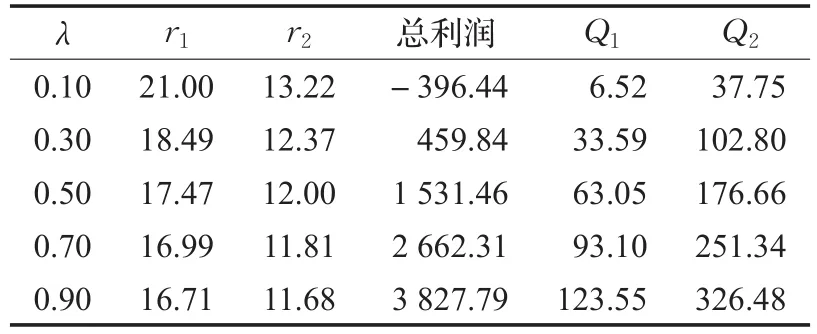
表9 推迟时隙1最迟预定时刻120的影响
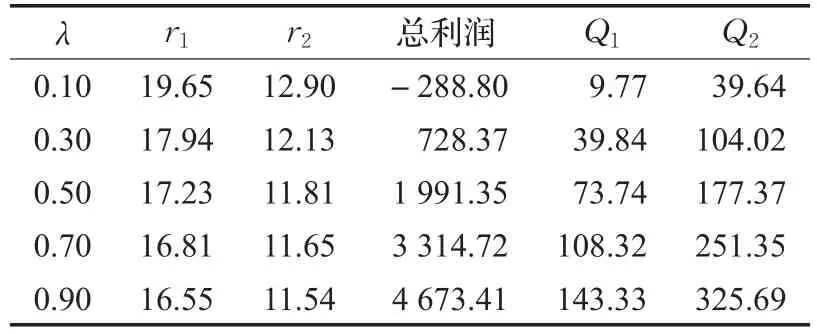
表10 推迟时隙1最迟预定时刻240的影响
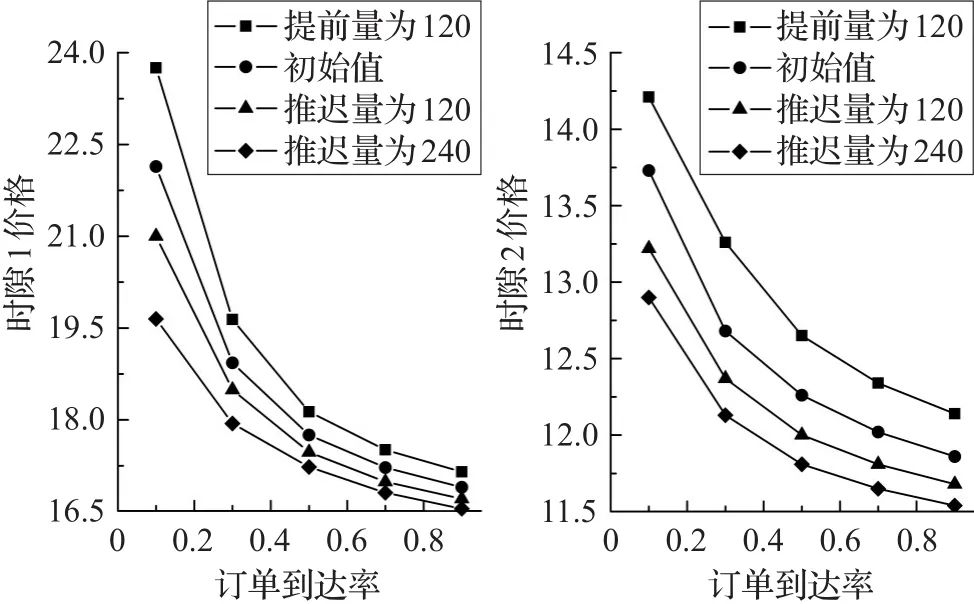
图5 在不同时隙1最迟预定时刻以及订单到达率下的价格
在不考虑时隙提前期的改变成本的前提下得到以下两点:首先,对比表7~表10以及结合图5可发现,在推迟时隙1的最迟预定时刻后,可看到最优时隙价格下降以及订单接受量增加,而在提前时隙1的最迟预定时刻后产生相反的结果。其次,在图6中纵向地可看到,在推迟时隙1的最迟预定时刻后,时隙的总利润增加,但在提前时隙1的最迟预定时刻后总利润减少。并且在订单到达率等于0.1处,总利润增加和减少的幅度较小,而当订单到达率等于0.9时总利润增加和减少的幅度才较大。

图6 在不同时隙1最迟预定时刻以及订单到达率下的总利润
总结以上两点后得到,在时隙最优价格策略以及不考虑时隙提前期变动成本的前提下,当运能较充沛时,较晚最迟预定时刻下的最优时隙价格应低于较早最迟预定时刻下的最优时隙价格。但时隙在较晚最迟预定时刻下预计接受订单量以及总利润大于在较早最迟预定时刻下的,并且总利润多出的部分大小与订单到达率成正相关联系。所以在初期规划时隙时,网络零售商可以考虑在订单到达率高的时段为时隙设置较晚的最迟预定时刻以提升总利润,而在订单到达率低的时段为时隙设置较早的最迟预定时刻以避免高额的运营成本支出。
5 结束语
本文研究配送时隙最迟预定时刻差异化背景下考虑时隙运营成本的时隙价格问题。在分析问题特点后构建出各订单到达阶段可选择时隙的集合,并结合MNL模型预测随订单到达阶段后移而改变的时隙选择概率,根据配送时隙的特点构建时隙运营成本模型。算例中分析了考虑时隙运营成本对时隙价格制定的必要性,并讨论了在不同的订单到达率下服务区域的差异和时隙最迟预定时刻的改变对网络零售商的意义,为网络零售商提供以下运营管理意见:在制定时隙价格时考虑时隙运营成本能使总利润更大;应对面积大而订单到达率低的地区制定较高的时隙价格,此时的价格对订单到达率波动很敏感,订单到达率上升时可以适当下调价格;应对面积小而订单到达率高的地区制定较低的时隙价格,此时的价格对订单到达率波动不敏感,订单到达率上升时可以保持时隙价格不变;网络零售商可以考虑在订单到达率高的时段为时隙设置较晚的最迟预定时刻,而在订单到达率低的时段为时隙设置较早的最迟预定时刻。
在今后的研究中会把本文中被最迟预定时刻分割的单订单到达周期扩展为多订单到达周期,希望利用马尔科夫决策过程原理和贝尔曼最优定理解决最迟预定时刻差异化背景下的动态时隙价格问题。同时,对配送时隙的成本进行更深入的探讨,使研究内容为当下以及未来的网络零售行业提供更加有用的建议。

