地震作用下钢筋混凝土桥墩残余位移研究
王军文, 李海洋, 闫聚考, 石 岩
(1.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,石家庄 050043;2.中信建筑设计研究总院有限公司,武汉 430014;3.石家庄铁道大学 大型结构健康诊断与控制研究所,石家庄 050043;4.兰州理工大学 土木工程学院,兰州 730050)
1995年日本阪神地震警告人们单一的最大延性位移不能够满足目前的桥梁抗震要求,桥梁的抗震设计应考虑残余位移的影响。为此,1996年日本道路协会将残余位移验算内容加入桥梁抗震设计规范[1];美国联邦应急署在FEMA 273(1997)与FEMA 356(2000)中也将残余偏移作为性能指标;在fib(2003)中提出的钢筋混凝土建筑基于位移的抗震设计中也强调残余偏移的重要性。我国目前对钢筋混凝土桥墩震后残余位移的研究刚刚起步,对影响残余位移的各种因素及计算方法缺乏系统研究[2]。因此,从残余位移的机理入手,抓住影响残余位移的主要因素,结合我国的桥梁抗震设计规范,提出精度更高的残余位移计算方法具有重要的现实意义。
为揭示地震作用下钢筋混凝土桥墩残余位移变形机理,许多学者进行了大量试验和理论研究。Kawashima等[3]指出残余位移比主要受双线性因子的影响,自振周期、位移延性系数对残余位移比的影响很小,地震震级、震中距、场地类别对残余位移比没有影响。Phan等[4]发现使用O-Hyst滞回模型预测的残余位移比使用Clough模型或Q-Hyst模型更接近试验结果。余波等[5]指出刚度退化和强度退化将导致非弹性体系的位移时程曲线偏移,从而引起残余位移改变;靳建楠[6]研究发现墩顶位移延性系数大于3后,纵筋粘结滑移对残余位移的贡献呈增大趋势。以上研究指出影响地震作用下钢筋混凝土桥墩残余位移的主要因素及其影响规律,但并未给出包含主要影响因素的残余位移预估公式。Risa等[7]推荐一种基于能力谱法求解残余位移的方法,但计算过程比较复杂,不便于应用。为此,本文基于残余位移影响因素的敏感性分析,建立了地震作用下钢筋混凝土桥墩残余位移影响系数的预测公式,对基于性能抗震设计时快速评估钢筋混凝土桥墩残余位移具有重要的参考价值。
1 残余位移延性指标
依据Hose等[8]提出的残余位移延性指标μRd进行残余位移系数分析,其计算公式如下
(1)
式中:dR1,dy1分别为桥墩正向加载的残余位移和等效屈服位移;dR2,dy2分别为桥墩负向加载的残余位移和等效屈服位移。
将日本桥梁抗震设计规范中对残余位移验算公式按残余位移延性指标表达,其计算公式为
dR=μRd·dy
(2)
μRd=cR(1-r)(μr-1)
(3)
式中:dR为桥墩的残余位移;cR为残余位移修正系数;r为钢筋强度硬化系数;μr为桥墩的位移延性系数;dy为桥墩的等效屈服位移。
由式(2)可知对残余位移的研究可归结为对残余位移延性指标μRd的分析。
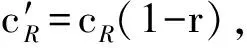
(4)


图1 桥墩残余位移延性指标
2 有限元建模及可靠性验证
2.1 有限元模型的建立
应用OpenSees软件对钢筋混凝土桥墩的抗震性能进行参数分析,采用纤维梁柱单元建立桥墩的有限元模型(图2),在塑性铰区单元适当加密;截面采用混凝土纤维单元和钢筋纤维单元模拟,混凝土本构关系为Kent-Park模型,采用Concrete01WithSITC材料模拟,钢筋本构关系为Giuffre-Menegotto-Pinto模型,采用Steel02材料模拟;在墩底增加一个零长度截面单元来模拟纵筋的粘结滑移,纵筋滑移采用Bond_SP01模型[10],墩底固结;墩顶施加集中质量模拟上部结构重量,其大小按恒载轴压比计算;阻尼采用瑞利阻尼,地震波的时间调整系数按桥墩的相似比计算[11]。

图2 桥墩有限元模型
2.2 可靠性验证
为了验证2.1节所建模型的可靠性,对Sakai等[12-13]所做的振动台试验进行数值模拟,由于篇幅原因,仅列出了Sakai完成的RC试件的计算与试验结果的对比(图3)。由图3可知,位移时程曲线试验结果和计算结果基本一致,说明采用2.1节建立的模型对钢筋混凝土桥墩进行非线性时程分析是可行的。

图3 Sakai振动台试验计算结果和试验结果的对比
Fig.3 Comparison of analysis and experimental results for Sakai’s shaking table test
3 残余位移延性指标的影响参数分析
采用2.1节的计算模型对Lehman等[14]完成的钢筋混凝土试件进行动力时程分析,选取的14条实测Ⅱ类场地下的地震波如表1所示,地震波的峰值加速度调整为0.4g,阻尼比取0.05,时间调整系数为0.577。
3.1 轴压比
利用Lehman完成的3个钢筋混凝土桥墩试件415、815、1015,假设轴压比ηk分别为5.0%、7.5%、10.0%、12.5%、15.0%、20.0%、25.0%、30.0%、35.0%,其他设计参数与拟静力试验相同,先计算出轴压比对残余位移延性指标的影响,然后通过计算残余位移延性指标与墩顶位移延性关系图中斜线的斜率,求出残余位移影响系数随轴压比变化的曲如图4所示。
由图4可知,残余位移影响系数随轴压增大而减小,轴压比大于20%后,残余位移影响系数基本不变。
3.2 长细比

表1 选用的地震波
选取Lehman完成的试件415,改变桥墩高度使其长细比λ分别为4、5、6、7、8、9、10,其他参数与拟静力试验相同,计算出残余位移影响系数随长细比变化的曲线(图5)。
3.3 纵筋配筋率
利用Lehman完成的3个桥墩试件415、815、1015,通过改变纵筋的直径来调整纵筋配筋率,使纵筋配筋率ρt分别为0.5%、0.85%、1.16%、1.52%、1.92%、2.37%、2.87%、3.41%,其他设计参数与拟静力试验相同,得出残余位移影响系数随纵筋配筋率变化的曲线如图6所示。由图6可知,残余位移影响系数随纵筋配筋率增大而增大,在纵筋配筋率大于1.5%后,残余位移影响系数基本接近水平。

图4 轴压比对残余位移影响系数的影响
Fig.4 Effect of axial load ratio on residual displacement influence coefficient

图5 长细比对残余位移影响系数的影响
Fig.5 Effect of aspect ratio on residual displacement influence coefficient

图6 纵筋配筋率对残余位移影响系数影响
Fig.6 Effect of longitudinal reinforcement ratio on residual displacement influence coefficient
3.4 体积配箍率
通过加密箍筋间距来增大体积配箍率,体积配箍率对核心混凝土本构的影响通过Kent-Park模型计算。选用Lehman完成的415、815、1015共3个试件进行体积配箍率分析,其体积配箍率ρv分别取0.35%、0.53%、0.70%、1.05%、1.40%、2.10%、2.80%,其他参数与拟静力试验相同,算出残余位移影响系数随体积配箍率变化曲线(图7)。

图7 体积配箍率对残余位移影响系数的影响
由图7可知,残余位移影响系数随体积配箍率增大而减小,但其变化幅度较小。
3.5 纵筋强度硬化系数
选取Lehman完成的815、1015桥墩试件进行地震作用下的纵筋强度硬化系数分析,其恒载轴压比为15.0%,纵筋强度硬化系数r分别为0、0.005、0.01、0.015、0.02、0.03、0.04,其他设计参数与拟静力试验相同,得出残余位移影响系数随纵筋强度硬化系数变化的曲线(图8)。
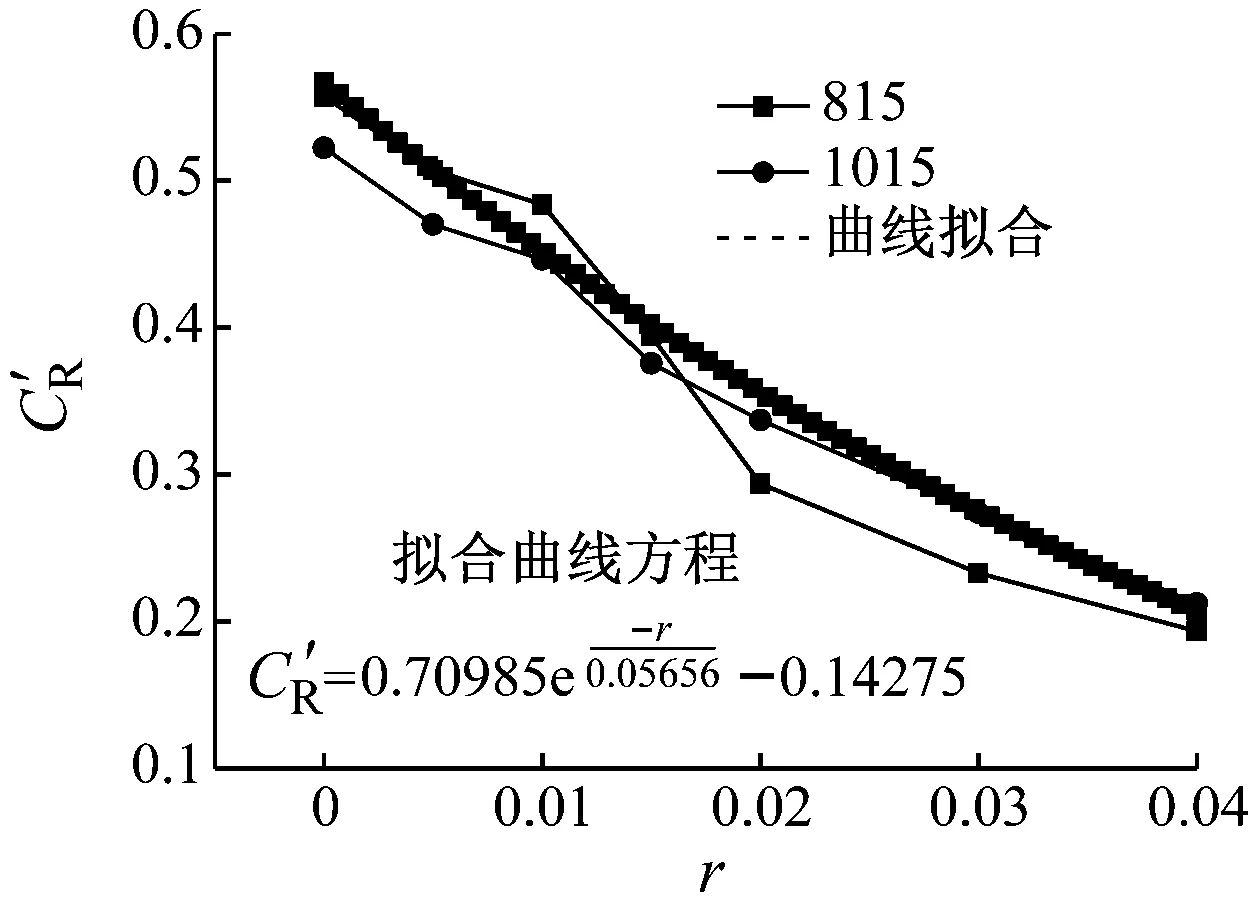
图8 纵筋强度硬化系数对残余位移影响系数的影响
Fig.8 Effect of of strength hardening coefficient of longitudinal reinforcement on residual displacement influence coefficient
由图8可知,残余位移影响系数随纵筋强度硬化系数增大而减小。
3.6 纵筋与混凝土强度比
选取Lehman完成的815、1015试件进行分析,混凝土抗压强度为36.5 MPa,改变纵筋的屈服强度使纵筋屈服强度与混凝土抗压强度比k分别为6.85、8.26、9.60、10.97、12.34、13.71、15.08、16.45,其他参数与拟静力试验相同,分析出残余位移影响系数随纵筋与混凝土强度比变化的曲线如图9所示。
由图9可已看出,残余位移影响系数随纵筋与混凝土强度比增大而增大。
4 残余位移影响系数预测公式

图9 纵筋与混凝土强度比对残余位移影响系数的影响
Fig.9 Effect of strength ratio between longitudinal reinforcement and concrete on residual displacement influence coefficient
由于地震作用下钢筋混凝土桥墩墩顶最大位移和残余位移存在一定的离散性以及长细比对桥墩残余位移的影响,本文偏于安全考虑,给出了以轴压比、纵筋配筋率、体积配箍率、纵筋强度硬化系数、纵筋与混凝土强度比为变量的残余位移影响系数的计算公式
(5)
式中:ηk为轴压比;ρt为纵筋配筋率;ρv为体积配箍率;r为钢筋强度硬化系数;k为纵筋与混凝土强度比。
利用式(5)计算Sakai等、Qu和Hachem等[15]完成钢筋混凝土桥墩的残余位移影响系数,通过残余位移延性指标计算桥墩的残余位移与试验值、日本规范计算值对比如表2所示。
表2残余位移计算值与试验值对比
Tab.2Comparisonofcalculatedvalueandexperimentalvalueofresidualdisplacement

试件试验值/mm日本规范本文公式计算值/mm偏差/%计算值/mm偏差/%SakaiX方向31.0 78.5153.247.151.8HachemA1序841.197.2136.357.740.3A2序415.538.4147.922.847.2序952.194.982.356.48.3B1序625.471.6182.042.567.4B2序1324.456.2130.633.436.9Kolleger序列363.3163.8158.868.68.5序列5110.1294.0167.0123.111.9注:偏差=(计算值-试验值)/试验值
由表2可知,本文公式对残余位移的估算值比日本规范更接近试验结果,且公式中包含影响桥墩震后残余位移的主要因素,更能体现残余位移的变化规律,因此本文预测公式可以用于基于性能抗震设计时初步估算地震作用下钢筋混凝土桥墩的残余位移值。
5 结 论
(1) 钢筋混凝土桥墩残余位移影响系数随轴压比、纵筋强度硬化系数、体积配箍率、长细比的增大而减小,在轴压比大于20%后残余位移影响系数基本不变。
(2) 桥墩纵筋配筋率、纵筋与混凝土强度比增大,残余位移影响系数增大,在纵筋配筋率大于1.5%后,残余位移影响系数基本不变。
(3) 建议公式中包含影响桥墩震后残余位移的主要因素,更能体现残余位移的变化规律,可用于基于性能抗震设计时桥墩残余位移的预估。

