含有时滞控制的准零刚度隔振器动力学分析
李东海, 赵寿根, 何玉金, 李 涛
(北京航空航天大学 航空科学与工程学院, 北京 100083)
振动隔离是解决工程振动问题的重要手段。在目前大量的工程实际中,普遍采用线性隔振器,对于一些精密仪器而言,如航天器上的光学元件,低频振动对其精度影响更大。如采用线性隔振措施,势必要降低隔振器的刚度从而实现低频隔振。这也会造成隔振器的静态稳定性降低。理想的情况是隔振器具有较高的静态刚度来保证静态负载能力,并且具有较低的动态刚度来增大隔振频率范围。高静态刚度低动态刚度(High-Static-Low-Dynamic-Stiffness, HSLDS)特性可以通过非线性结构来实现[1]。Ibrahim[2]综述了非线性隔振器的发展,表明非线性隔振是一个十分活跃的领域。Liu等[3]在其综述中也详细地阐述了非线性隔振器在微振动隔离领域的应用。Yang等[4]研究了带有负刚度机构的非线性隔振系统的动力学行为。研究表明增加负刚度机构能极大地扩展隔振频带,并且非线性隔振系统的功率流特征结果也表明增加负刚度能使系统具有更好的隔振性能。Shaw等[5]用双稳板来制作轻而有效的高静态低动态刚度的隔振系统,可以采用非线性刚度元件来实现准零刚度(Quasi-Zero-Stiffness, QZS)特性[6]。彭献等[7]采用连杆机构作为负刚度调节机构,研究了准零刚度隔振器的设计方法。Zhang等[8]将欧拉压杆作为负刚度调节机构,设计了正负刚度并联的隔振系统。Carrella等[9-12]利用斜置弹簧产生负刚度特性,并与正刚度弹簧相并联组成准零刚度隔振器,并详细地研究了隔振器的静动态特性。Xu等[13]利用电磁弹簧作为负刚度元件,设计了一种准零刚度隔振器,其隔振性能在低频区域,超过了等价的线性隔振器。由于准零刚度具有高静态刚度低动态刚度,可以有效地克服传统非线性隔振器增加隔振频率范围和保证静态承载力之间的矛盾,近年来,针对准零刚度隔振器的研究变得越来越热门。
准零刚度隔振器有着线性隔振器不可比拟的优点,那就是隔振频率范围广,静态刚度高。但是相比线性隔振器而言,其共振峰值依然被认为是过大;由于准零刚度隔振器的固有的非线性,所以会造成系统的跳跃现象,这种系统的不稳定性是一种不安全因素所以在工程实际应用中不期望出现的。因此为了获得更好的隔振性能,开展准零刚度隔振器的主动控制策略的研究就显得十分必要了。准零刚度隔振器的动力学特性方程可以用具有三次非线性项的Duffing振子模型来描述[14-17]。目前针对准零刚度隔振器的主动控制研究相对较少,但是许多学者开展了对Duffing振子和吸振器的主动研究[18-21]。在吸振器的主动控制研究中,学者主要采用了时滞控制的策略,这是因为在实际应用中,控制器和作动器会有不可避免的时间滞后,所以在研究控制策略的时候,将时滞效应纳入考虑范围之中。Zhao等[22]将时滞控制策略应用于双自由度非线性吸振器中,来抑制垂直位移方向的振动,其研究成果表明,采用时滞正反馈的非线性吸振器可以有效地抑制大约65%的垂直振动,而采用负时滞反馈的吸振器可以吸收86%的振动。但是针对准零刚度隔振器的时滞控制研究相对较少,本文在之前的研究基础上,对准零刚度隔振器施加线性位移时滞控制,并对其静力学特性进行分析,在力激励的情况下,利用平均法对隔振器的动力学特性进行理论推导,并分析了隔振器增加时滞控制后的稳定性,以及发生跳跃现象和Hopf分叉现象的临界条件。
1 准零刚度隔振器动力学模型
1.1 准零刚度隔振器
本文采用两个斜置弹簧作为负刚度元件与竖直的正刚度弹簧相并联形成单自由度的准零刚度隔振器。对其进行线性时滞位移主动控制的结构模型如图 1中,当隔振器受载后,斜置弹簧处于水平位置并达到静平衡点处。其长度为l。自由状态时,此时质量m距离静平衡位置的距离为xs;x为负载质量m从静平衡位置开始的位移。斜置弹簧的原长为l0。斜置弹簧的刚度为kh,垂直弹簧的刚度为kv,假设系统的阻尼为线性阻尼,阻尼系数为c,控制刚度为kc,反馈信号为系统的线性位移x;f为负载质量m受到的外界激励力。
1.2 准零刚度隔振器动力学分析
准零刚度隔振器线性位移时滞控制结构示意图如图 1所示。为了建模的简便性,先考虑无控制系统的动力学特性。利用拉格朗日方程可以建立准零刚度隔振器的动力学方程。

图1 准零刚度隔振器线性位移时滞控制结构示意图
隔振器的动能为
(1)
现设静平衡位置为系统的势能零点,则该系统的总势能为
(2)
拉格朗日函数可以表示为
(3)
拉格朗日方程表示为
(4)
式中:F(t)为隔振器受到的外界激励力;t为时间。
联立式(3)和式(4)可得到隔振器的动力学微分方程
(5)
引入无量纲参数,可对式(5)无量纲化,得到隔振器的无量纲动力学方程
(6)

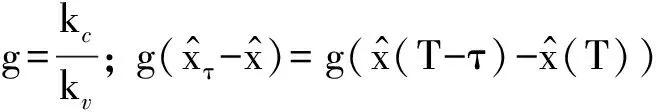
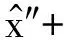
(7)
当隔振器的响应位移相对初始垂向长度为小量时,可以将系统的动力学方程在静平衡点处展开并保留三次精度,将系统的动力学方程转化为类似于Duffing方程的形式来研究。对式(6)应用泰勒展开并保留三阶精度,得到
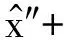
(8)
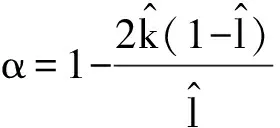
(9)
由式(9)可以清晰地看出来,系统具有三次非线性项,可以利用Duffing方程的部分特性来研究其特性。
2 简谐力激励下的系统的响应
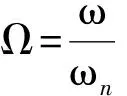
(10)
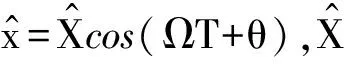
(11)
在式(11)中
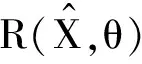

将ΩT+θ在0-2π之间取平均值[23]得到
(12)

(13)
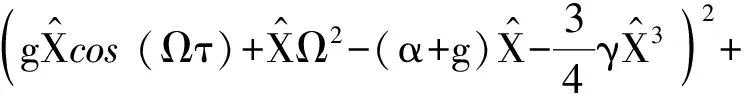
(14)
相频特性为
tanθ=
(15)
为了更清楚地分析线性时滞位移反馈对系统动态响应的影响,定义受控系统的等效阻尼系数和等效线性刚度比分别为

(a) 幅频响应曲线(b) 相频响应曲线
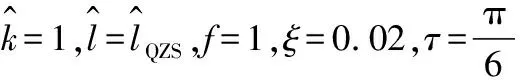
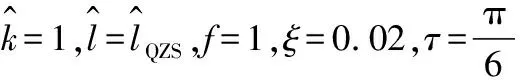

(a) 幅频响应曲线(b) 相频响应曲线
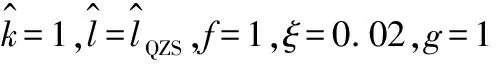

(16)
αeq=α+g(1-cos (Ωτ))
(17)
当g=0,sin (Ωτ)>0时隔振器处于不受控状态,隔振器主振动共振峰值响应很大,而当g≠0,sin (Ωτ)>0时,共振峰值被有效地抑制,这种现象也可以在图 2中体现出来。这就很好地说明了线性位移时滞反馈的阻尼效应。而当sin (Ωτ)<0时,系统的等效阻尼减小,共振峰值相比不受控系统增大。

(18)
αeq=α+g(1-cosτ)
(19)
这样可以近似认为在共振区域内,等效阻尼比和等效线性刚度比是周期为2π周期函数。因此时滞参数τ的取值范围为τ∈(0,π),在该范围内系统的等效阻尼总是大于不受控系统的阻尼。
3 准零刚度隔振器稳定性分析
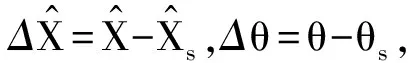
(20)
可得系统的扰动方程为
(21)
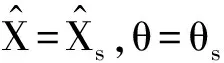
系统的稳定性可以通过线性扰动方程式(21)的特征方程来分析
(22)
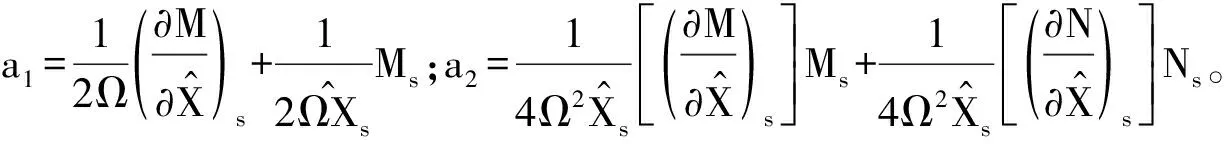
当a1>0,a2>0,则奇点渐近稳定;当a1>0,a2<0时,奇点不稳定。所以a2=0为稳定性边界。注意到a1的取值和系统的非线性项无关,实际上a1代表着有控制时线性自由振动的稳定性,稳定性独立于激励、响应幅值等。当a1=0意味着特征方程会有一对纯虚根出现,因此会出现Hopf分叉[26-28]。
由a2=0可得稳定性边界为
(23)
其中a=gcos (Ωτ)+Ω2-(α+g);b=gsin (Ωτ)+2ξΩ
(24)
(25)
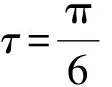

(a) g=0(b) g=1
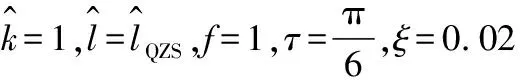
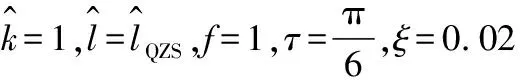

(a) τ=0(b) τ=π6
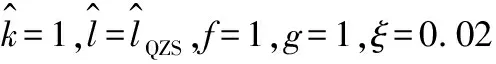
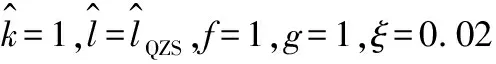
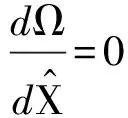
(26)
为了更加直观地说明(f,g)的取值对隔振器跳跃现象的影响,可取不同的(f,g)绘图说明。当(f,g)的取值为(0.4, 0.1)时,处于区域2中,隔振器不会发生跳跃现象;当(f,g)的取值为(0.4, 0.3)时,处于区域1中,系统会发生跳跃现象。隔振器的响应曲线如图 7所示。
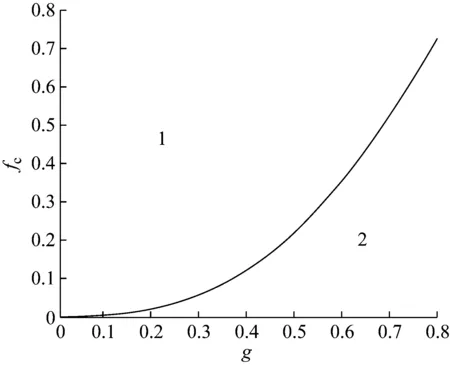
图时跳跃现象临界曲线

(a) (f,g)=(0.4,0.1)(b) (f,g)=(0.4,0.3)
图7 当无量纲外界激励力的幅值f和控制增益参数g处于区域1和2中时隔振器的响应特性
Fig.7 The response characteristic of the isolator when non-dimensional excitation amplitudefand control gain g are fixed in region 1 and 2 respectively
由临界条件a1=0得到
gsin (Ωτ)+2ξΩ=0
(27)
可以得到在参数(g,τ)平面内Hopf分岔的边界。对于自由振动的线性系统,其幅频特性为
(28)
将式(27)代入式(28)中,得到
gcos (Ωτ)+Ω2-(α+g)=0
(29)
将式(29)与(27)联立,得到频率比和临界时滞参数的表达式如式(30)所示。式(30)所控制的曲线为系统发生Hopf分岔的边界。
(30)
如图 8所示为Hopf分叉的边界曲线。当(g,τ)取值在参数平面A中,则特征方程式(22)的特征值的实部为负,系统的运动随着时间衰减;当(g,τ)取值在参数平面B中,特征值的实部为正,系统会作由Hopf分叉引起的周期振动,造成系统平衡点的不稳定;而当(g,τ)取值恰好位于曲线之上时,特征值的实部为零,为发生Hopf分叉的临界条件。
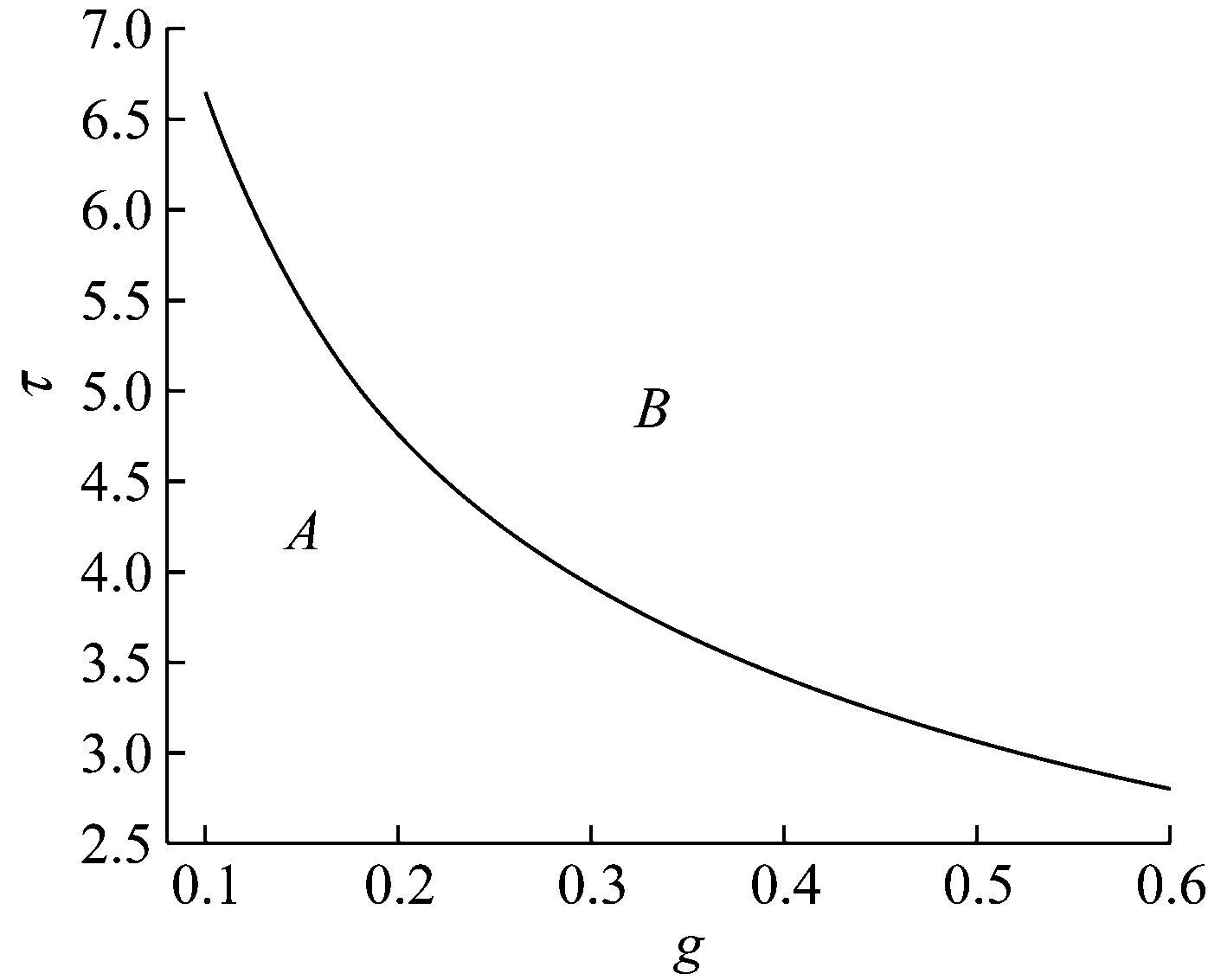
图时的Hopf分叉临界曲线
4 结 论
本文研究了含有线性位移时滞控制的由三弹簧组成的准零刚度隔振器在简谐力激励下的动态响应与稳定性特性。通过李雅普诺夫线性近似稳定性理论和劳斯-赫尔维茨准则研究了系统的稳定性和系统的跳跃现象以及Hopf分叉现象,理论分析表明,在系统发生跳跃现象的频率带内,为系统的不稳定区域,同时给出了系统的稳定性边界。在此基础上讨论了该类型隔振器系统增加时滞控制时的动力学特性,结果表明有线性位移时滞控制时可以有效地抑制系统响应幅值,同时进一步研究了时滞参数与控制增益对响应的影响,定义了等效阻尼和等效线性刚度系数,给出了时滞控制参数的取值范围,讨论了时滞控制对系统的阻尼和刚度的影响,从研究和讨论得到的结果看出准零刚度隔振器在给出控制参数的范围内,受控系统的动力学响应特性比不受控系统性能更为优越。

