基于三维声场空间特征的故障诊断方法研究
侯俊剑, 吴艳灵, 何文斌, 房占鹏, 肖艳秋
(1. 郑州轻工业学院 机电工程学院, 郑州 450002; 2. 河南省机械装备智能制造重点实验室, 郑州 450002)
机械噪声是机械振动通过媒介向外界传播的结果,蕴含着丰富的机械状态信息[1]。利用噪声信号进行故障诊断的声诊断技术具有非接触测量和操作简便的优点,是振动故障诊断的有益补充[2-3]。侯俊剑等[4]提出了一种声像故障诊断方法,通过阵列测试和声成像算法重建声源表面二维声压分布,利用图像处理技术提取声像特征并进行状态诊断,为声诊断提供了新的思路。该方法改善了传统的基于单点测试的声诊断鲁棒性,但诊断过程中仅考虑源面(声源表面)的声压幅值分布,忽略了相位信息,信息利用不足,在局部声压幅值变化较小的弱故障工况下存在识别率低和诊断困难等问题。针对上述问题,本文提出一种基于三维声场空间特征的故障诊断方法。通过阵列测量和近场声全息技术(Near Field Acoustic Holography,NAH)重构三维声场,把声源表面的幅值和相位信息映射到空间域,然后提取声场的三维空间特征进行诊断识别。
基于三维声场空间特征的诊断方法逆向利用医学领域X射线分层构建三维模型的思想[5],将整个三维辐射声场进行空间断层切片处理。声音是周期信号,仅考虑源面法向一个波长范围的空间声场,等间隔序列拾取13个辐射声场空间断层,得到声场各断层切片的声压幅值分布,构建声场的空间变化序列模型。三维声场空间序列模型从空间维度融合了源面的幅值和相位信息,比二维源面声像蕴含的故障信息更丰富,能够有效提高弱故障工况诊断的识别效果,进一步完善基于声像技术的故障诊断方法。
1 基于三维声场空间特征的故障诊断方法
1.1 方法流程
基于三维声场空间特征故障诊断方法的诊断流程,如图1所示。设定样本和待诊机械状态,采用阵列测量技术采集噪声信息,并利用近场声全息技术获得由序列三维空间断层切片构建的三维声场。序列提取各空间切片的Gabor小波特征,合并构建声场的空间特征模型。通过样本特征量结合支持向量机训练分类得到最佳分类器参数,并用于待诊机械的故障诊断。
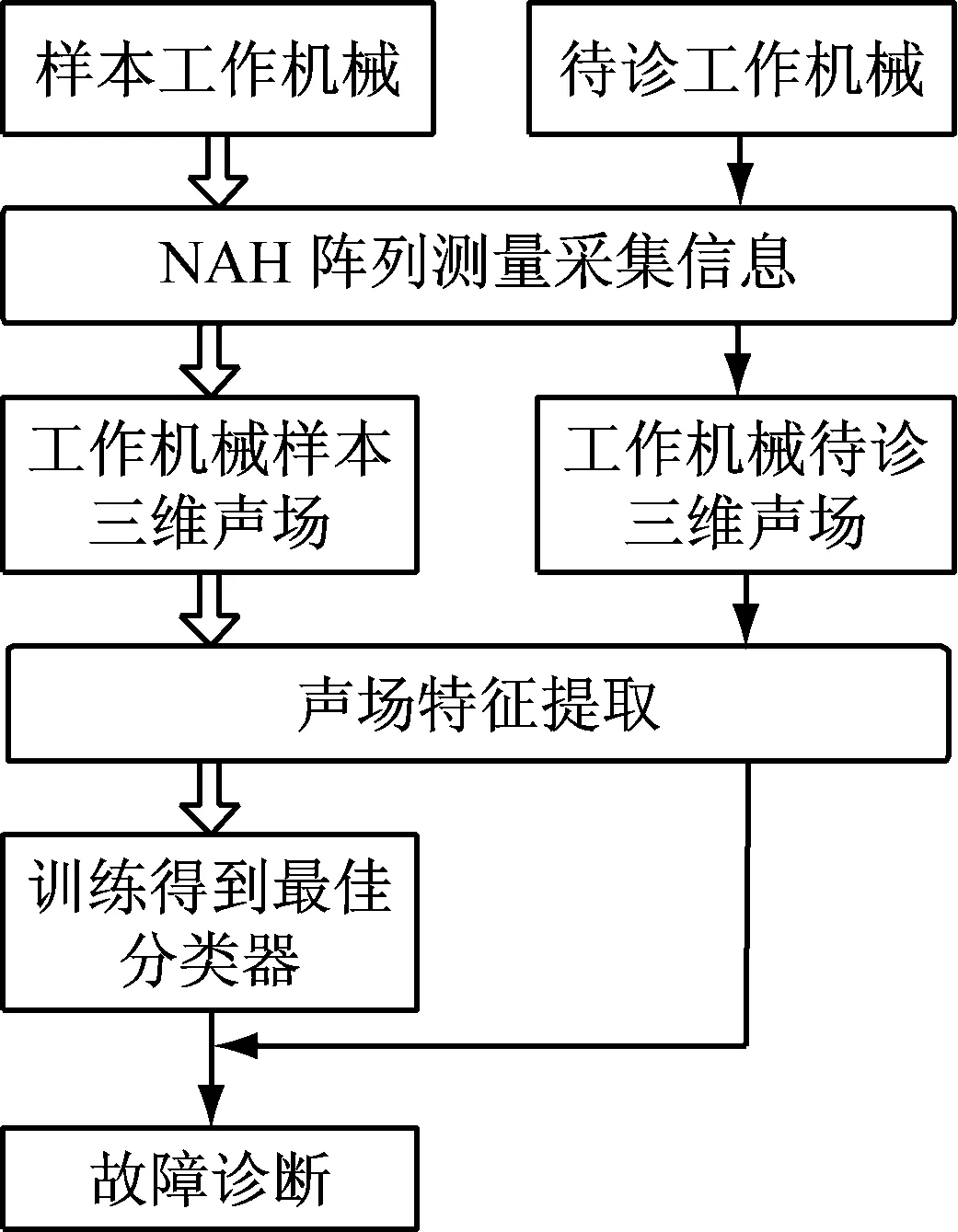
图1 三维声场空间特征的故障诊断流程
1.2 近场声全息(NAH)
近场声全息是典型的声场可视化技术,通过在包围声源的全息测量面上测量声压,然后借助源表面和全息面之间的空间场变换关系,由全息面声压重建源面的声场[6],其成像原理如图2所示。

图2 NAH空间变换示意图
本文采用平面正交共性NAH技术,全息面和测量面均为平面,假设全息面Sh位于z=zh,重建面Sc位于z=zc,声源面Ss位于z=zs,Sh和Sc上的声压分别为φ(x,y,zh,f)和φ(x,y,zc,f),f为重建频率。给定满足Dirichlet边界条件的格林函数GD(x,y,zh-zc,f),可得广义重建式[7]
φ(x,y,zc,f)=
(1)
(2)
(3)
(4)
式中:F表示二维空间傅里叶变换;上标-1表示逆变换;kx,ky分别是沿x,y方向上的空间波数。
1.3 特征提取
图像特征主要体现在纹理信息和形状信息等方面,机械在弱故障工作状态下,图像形状变化不显著、隐匿性高,而图像的纹理信息可充分反映图像的局部统计特征和局域属性变化。文献[8-9]研究表明Gabor小波特征能够有效体现纹理变化,获得较好的诊断效果。
母小波为Gabor函数的小波变换,可同时在空域、频域和方向上获得最佳分辨率[10],非常适合于细节纹理的特征提取。假设用f(x,y)表示尺寸为M×N的图像,则该图像的二维离散Gabor小波变换为
(5)
式中:s和t是滤波器掩模尺寸变量;x和y指明像素在图像中的位置;p和q分别表示小波变换的尺度和方向;φp,q是Gabor小波变换函数。
尺度为p、方向为q的能量信息E(p,q)为
(6)
E(p,q)虽可有效地表示纹理特征,但使用能量信息易造成分类误差[11],本文采用均值μ(p,q)和标准差σ(p,q)描述图像纹理特征
(7)
(8)
本文P和Q分别取常用值5和6[12-13],所提取的Gabor小波纹理特征向量表示为
Gabor=[μ0,0,σ0,0,μ0,1,σ0,1,…,μP-1,Q-1,σP-1,Q-1]
1.4 支持向量机

(9)
式中:φ为核空间映射函数;w为权矢量;b为偏置量;ζi为误差变量,即松弛因子,代表允许一定程度错分的系数;C为惩罚系数,用来折中考虑最小错分样本和最大分类间隔。
本文的SVM程序主要采用了台湾林智仁教授的Libsvm,该程序具有较高的知名度和通用性。在识别过程中,随机抽取4/5的样本作为训练样本,余下的1/5作为测试样本。通过网格搜索和交叉验证技术,以最小化均方差为目标函数训练样本库得到最佳分类参数,以优化后的参数对测试样本进行模式分类,实现故障诊断。使用5重交叉验证,并以5次识别率的平均值作为最终的识别效果。
2 相干声场状态诊断的仿真实验
机械在某一转速工况下多个部件会同时向外辐射噪声,且各部件声压幅值不尽相同,易产生相干声场。当某一部件发生故障时,其辐射声压幅值会产生变化,进而引起整个声场的分布变化。仿真采用两个同频声源来模拟相干声场,假设其中一个为重要零部件产生的声源,另一个为干扰源,通过设定重要声源的微弱变化来模拟弱故障工况。
2.1 仿真工况设置
两个声源尺寸均为0.05 m×0.05 m、声源1中心坐标(-0.125 m,0.025 m)、声源2中心坐标(0.125 m,0.025 m),其声源分布和全息测量面如图3所示。其中全息测量面尺寸为0.7 m×0.7 m,全息测点为15×15,声源重建面尺寸0.5 m×0.5 m。仿真通过调整声源振速幅值来模拟正常状态和故障状态,设定工作频率为300 Hz,弱故障工况下声源振速幅值与正常状态相差不大,正常状态下重要声源1振速幅值在0.012~0.017 m/s范围变化,故障状态下振速幅值分别在0.009~0.011 m/s和0.018~0.02 m/s范围内变化,正常和故障工况各取6个样本;干扰源2振速幅值在0.05~0.1 m/s范围内变化,从中选取6个样本。因此,仿真实验共模拟6×6=36种正常状态和6×6=36种故障状态。
300 Hz声源的波长为1.15 m,在声源表面法向一个波长范围内序列拾取13个声场空间断层切片,各断层切片尺寸与声源重建面(源像)尺寸相同,与声源面的距离如表1所示。
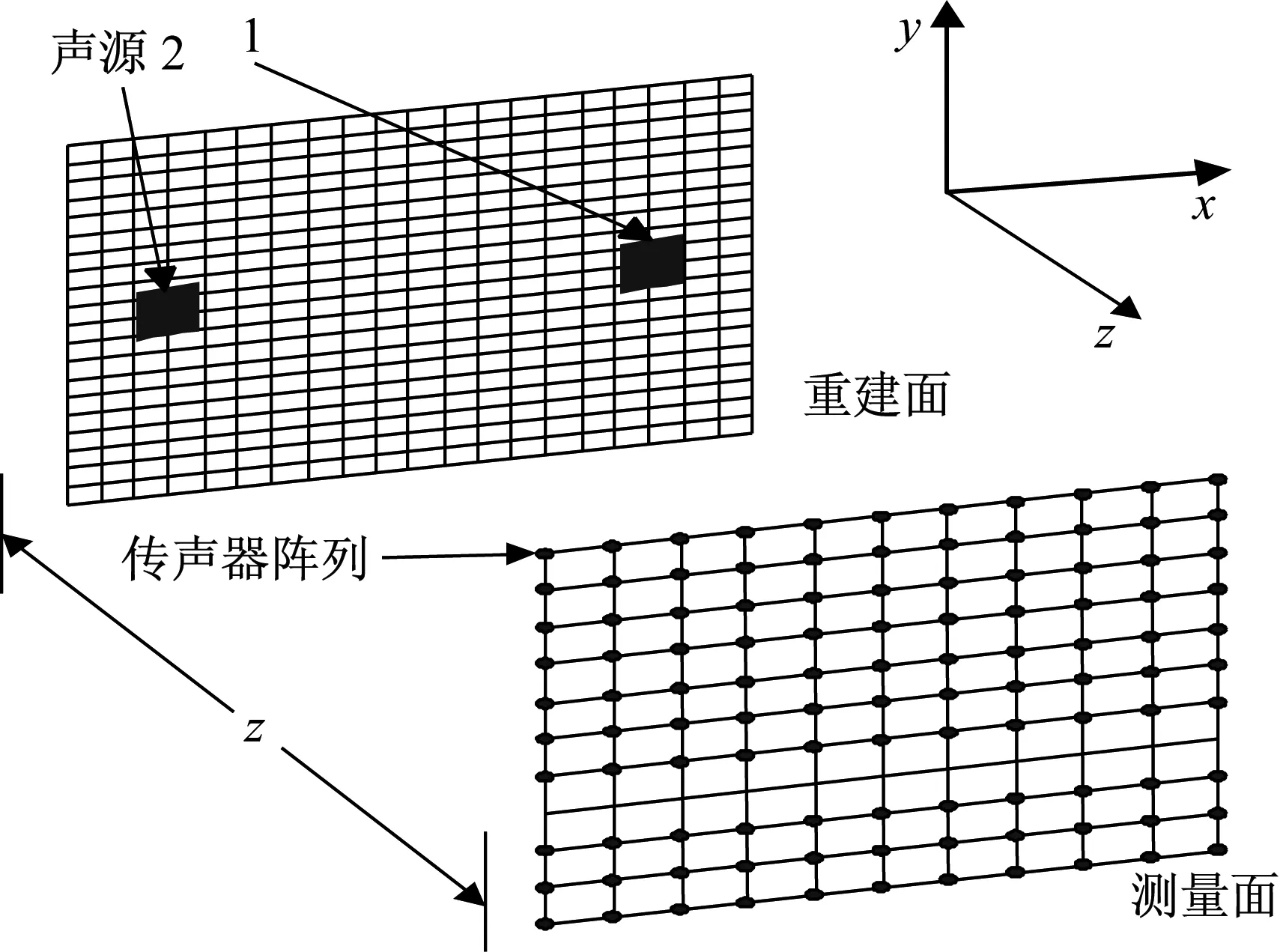
图3 声源分布及测量面、重建面的示意图

表1 各断层距声源面的法向距离
2.2 仿真结果分析
正常和故障状态下某2个样本的源面声像如图4所示,声场的空间切片分布如图5所示。源像图中声源1和声源2位置能够准确定位,但由于干扰源2声压幅值较大,几乎淹没声源1,使得声源1的微弱变化在声像图中无法辨识。通过对比图5的2~4空间切片声压分布,可以看到声压分布有一定的变化。

(a) 正常状态(b) 故障状态
图4 正常和故障状态下源面声像
Fig.4 Acoustic images obtained under the normal and fault conditions

(a) 正常状态

(b) 故障状态
Fig.5 Sound pressure distributions of 13 sections in radiation sound field under the normal and fault conditions
不同位置处断层声压分布包含的故障信息不同,不同空间断层组合所包含故障信息的冗余程度也是不同的。从13个断层中取出指定个数重新结合称为断层组合,当指定个数为n时(1≤n≤13),从包含源面在内的13处空间断层切片内任意挑选n个进行组合,利用组合的特征进行诊断分析,并把指定数n内所有组合诊断效果最高的识别率作为断层组合个数为n时的识别率。基于穷举法思想,对不同灰度级和断层组合提取Gabor小波特征,进而利用SVM进行分类识别,各灰度级下,识别率随断层组合的变化如图6所示。其中源面处的识别率为采用二维声像诊断技术得到的结果,在灰度级为32级时得到最高识别率88.9%。采用本文提出的基于三维声场空间特征进行诊断识别时,在灰度级为128,断层组合数n分别为4、5、6、7、8、9、10时,都能达到最高98.6%的识别率。
对比各灰度级和断层组合识别效果可以看到:
(1) 基于三维声场空间特征的故障诊断方法对弱故障工况诊断非常有效,识别率最高可达98.6%,比二维声像诊断技术最高识别率提高了10%。

图6 仿真工况下识别率随灰度级和断层组合数的变化
Fig.6 The recognition rates vary with the section groups and different grayscales under simulation conditions
(2) 各灰度级下,对比源面和断层组合个数为1时的识别率,源面的识别率普遍较低,即在辐射声场中存在一个观测面包含机械弱故障状态信息较完全,能够更好反映机械状态,进行故障诊断。
(3) 各灰度级下,识别率随断层指定组合个数的变化整体呈现先增加后降低的趋势,存在识别率最优的断层组合个数。即断层组合个数不是越多越好,亦不是越少越好。过少包含机械状态信息少,过多则有大量信息冗余,均影响识别效果。
(4) 灰度级的选择也对识别率影响较大,低灰度级会弱化图像中的纹理信息,进而损失部分反映机器运行状态的细节特征,降低识别精度。而高灰度级则会增加图像冗余纹理信息,同样会降低识别精度。因此,针对不同故障和声压分布状态,对应着不同的最佳灰度级。
(5) 基于二维声像诊断技术得到的最佳灰度级对于本文提出的诊断方法可参考性较差,因为断层组合同样蕴含丰富故障信息,当图像灰度级和断层组合的有效信息和冗余信息达到一定平衡后,就会获得最佳诊断效果。
3 音箱实验及结果分析
为进一步验证基于三维声场空间特征诊断方法的有效性和仿真实验结论,在空旷的混响厂房环境中进行了音箱实验。
3.1 实验台搭建
实验由Agilent 81150A高精度脉冲发生器产生频率为300 Hz正弦信号,功率放大器调节信号强弱,LMS信号采集系统阵列测量声压信号,进而利用近场声全息技术重构空间声场。其实验流程如图7所示,音箱及传声器分布如图8所示。实验采用线阵扫描方法,传声器线阵每间隔0.05 m布置一个传声器,长0.7 m共布置15个传声器,线阵水平扫描方向步长0.05 m,共15步长0.7 m,因此全息测量面0.7 m×0.7 m。测量面与音箱表面距离Z=0.05 m。
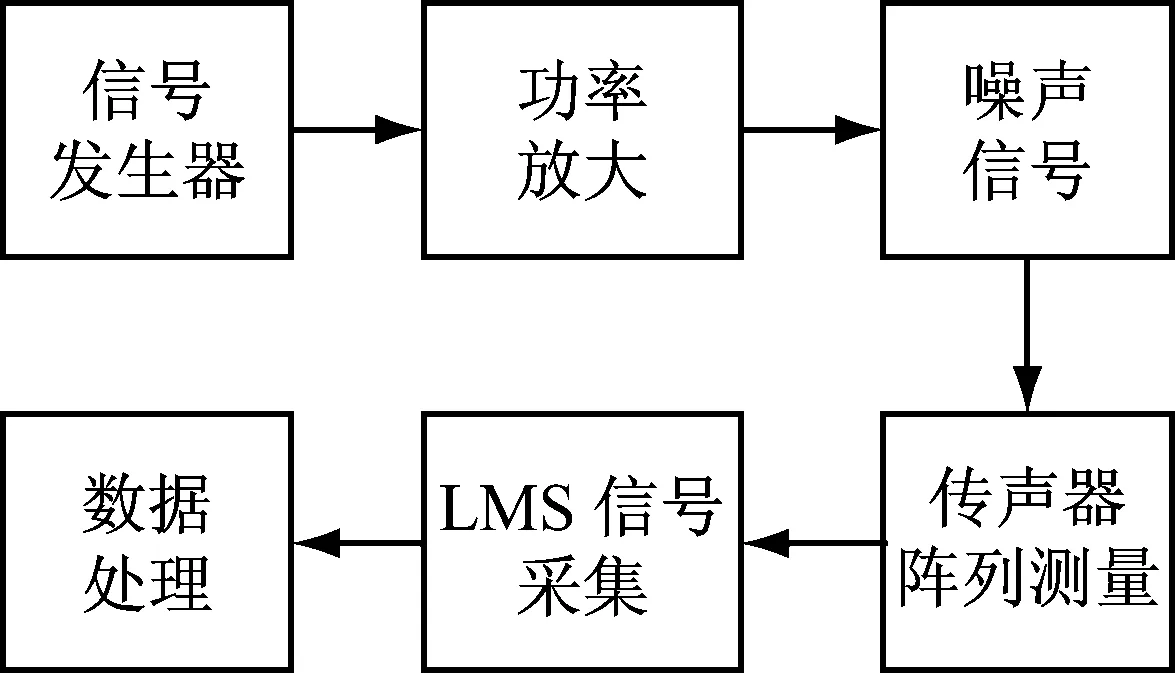
图7 实验流程

图8 音箱及传声器布置
3.2 实验工况设定
通过调节距离音箱中心法向距离0.05 m处的声压级大小来模拟不同工况:
(1) 音箱1作为重要声源,其声压级在77~80 dB之间变化时处于正常运行状态,随机选取6个样本;声压级75~76.5 dB和80.5~81.5 dB均为故障状态,在两个声压级范围内各选取3个样本,共6个故障样本。
(2) 音箱2作为干扰声源,其声压级在90~96 dB之间变化,实验在声压级范围内选取6种干扰状态。
因此,正常和故障状态各为6×6=36种。
3.3 实验结果
正常和故障状态下某2个样本的源面声像如图9所示,声场的空间切片分布如图10所示。在正常和故障工况状态下,源面声像图中干扰声源2位置能够准确定位,重要声源1因声压级较小被淹没,使得两种状态的声像图变化不大。对比图10中正常和故障状态下3~7的断层切片声压分布有较为明显的变化。

(a) 正常状态(b) 故障状态
图9 正常和故障状态下源面声像
Fig.9 Acoustic images obtained under the normal and fault conditions

(a) 正常状态

(b) 故障状态
Fig.10 Sound pressure distribution of 13 sections in radiation sound field under the normal and fault conditions
音箱实验结果如图11所示,其中基于二维声像诊断技术在灰度为128级时得到的最好识别效果为88.9%,基于三维声场空间特征进行诊断识别时在灰度为64级和断层组合数为2时的最高识别率为97.2%。实验结果与仿真结果非常吻合,表明了基于三维声场空间特征诊断方法的有效性和可行性,同时也验证了弱故障工况下该方法比二维声像诊断方法具有更好的鲁棒性。
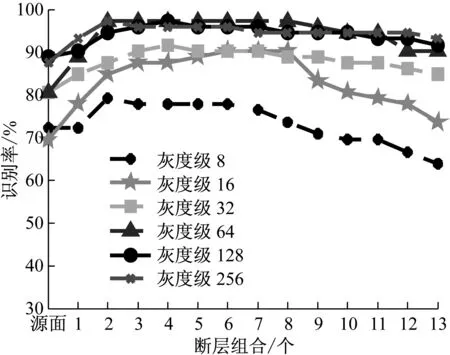
图11 实验工况下识别率随灰度级和断层组合数的变化
Fig.11 The recognition rates vary with the section groups and different grayscales under experiment conditions
4 结 论
基于三维声场空间特征的故障诊断方法进一步改进了二维声像诊断技术,通过映射声源的幅值和相位信息到三维空间声场,构建机械声场三维全息诊断模型进行诊断分析。仿真和实验结果都表明基于三维声场空间特征的故障诊断方法对声源声压幅值变化不大的弱故障工况诊断效果明显,验证了基于三维声场空间特征故障诊断方法的有效性和可行性。由于将二维声成像诊断技术拓展到三维声场,进一步拓展了声成像技术的应用,为弱故障工况的诊断提供了新的思路,并丰富了声学故障诊断。

