手枪弹对带UHMWPE软防护明胶靶标冲击效应的数值分析

孙 非， 马 力， 朱一辉， 徐 诚

(1. 南京理工大学 机械工程学院， 南京 210094； 2. 63856部队， 吉林 白城 137000)

超高分子量聚乙烯纤维(UHMWPE)具有重量轻、比强度高和比模量高等特性，通常被用来制作防护手枪弹的软质防弹衣,尽管该材料可以阻止手枪弹的侵彻作用，但仍会对有生目标的机体产生非贯穿钝击伤，开展手枪弹侵彻带纤维软防护机体靶标的非贯穿钝击伤产生机理研究，对软质防弹衣结构和材料的改进设计、以及软防护状态钝击伤的医学诊疗具有一定指导意义。

非贯穿钝击伤可以采用带防护的生物靶标和带防护的明胶模拟靶标进行研究，生物靶标内部冲击响应难于测量，试验重复性差。10%明胶材料密度肌肉相同，力学性能与肌肉相似，具有性能稳定、埋设传感器和高速摄像测量方便等优点，常常被用作有生目标的模拟物，故带防护的明胶模拟靶标在创伤弹道学研究非贯穿钝击伤中广泛应用[1-3]。Jacobs等[4]通过试验获得了UHMWPE材料抗弹性能；黄拱武[5]数值模拟了9 mm手枪弹作用下软质防护的明胶模拟靶标的动力学响应现象；Roberts等[6-7]建立了手枪弹高速撞击带软质防护的人体靶标计算模型，徐诚等[8]建立了步枪弹高速撞击带硬质防护的人体靶标计算模型[8]，分别数值模拟了不同枪弹非贯穿钝击作用下人体靶标的瞬态响应过程，获得了与试验在量级上相当的结果。Luo等[9-12]研究了手枪弹和步枪弹侵彻带防护的明胶模拟靶标问题，初步获得了枪弹高速撞击带防护的明胶模拟靶标的瞬态响应特性。但现有的研究工作并未全面掲示“手枪弹对带纤维软防护明胶靶标冲击响应机理”，特别是多种力学响应的定量关系，对于瞬时空腔和压力波数值模拟的精度也有待提高，鉴于此，本文通过试验与数值模拟相结合方法深入研究手枪弹对带纤维软防护明胶靶标冲击响应问题，建立更精确的数值计算模型，采用LS-DYNA进行计算获得多种力学响应的定量关系，对该问题的冲击响应机理提供新见解。

1 研究对象与方法

1.1 研究对象

本文主要研究7.62 mm手枪弹高速撞击带软防护(UHMWPE)的明胶模拟靶标过程，如图1所示，7.62 mm手枪弹由弹芯和弹头壳组成，撞击靶标的速度约为450 m/s。模拟靶标由UHMWPE软防护和明胶组成，如图2，软防护尺寸为300 mm×300 mm×9.2 mm，由46层纤维薄层重叠而成，每层纤维层的厚度为0.2 mm，总厚度为0.92 cm。明胶块采用10%明胶,尺寸为300 mm×300 mm×300 mm。

图1 7.62手枪弹几何模型

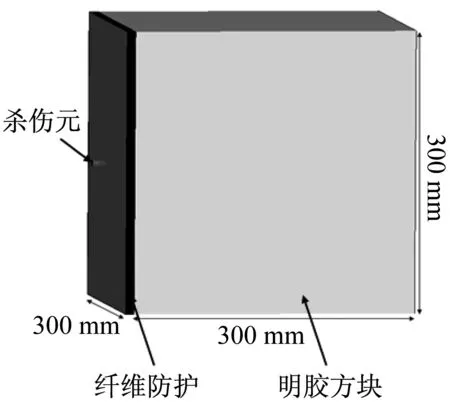
图2 带UHMWPE软质防护的明胶模拟靶标

1.2 有限元计算模型

1.2.1 UHMWPE软防护有限元模型

在手枪弹高速撞击带UHMWPE软质防护的明胶模拟靶标时，材料变形和破坏主要集中在撞击点附近，而其余区域未有明显变化，故在软防护的网格划分中，选择薄壳单元(SHELL163)，首先对单层纤维软防护进行网格划分，在撞击点区域划出半径为2 cm的网格密集区域，其余区域的网格则沿径向逐步变疏，如图3所示。而后，通过复制的方法，复制出余下的45层纤维层的网格，使得每一纤维层平面的相应位置的网格尺寸一致，所得计算网格如图4所示，软防护网格数为143 520。

图3 单层纤维防护的网格示意图

由于超高分子量聚乙烯纤维在软防护中的纤维束正交铺设，具有正交各向异性特性，当x,y,z为弹性主方向时，其应力应变关系可简化为

(1)

式中：E1，E2，E3为x，y，z主方向的弹性模量；v12，v21为泊松比；G23，G31，G12为剪切模量。

有限元模型中超高分子量聚乙烯纤维(UHMWPE)软防护采用复合材料壳失效材料模型(MAT_COMPOSITE_FAILURE_SHELL_MODEL)，该模型将材料视为弹塑性模型，材料模型分为弹性和塑性两段，采用Hooke定律定义弹性段的应力；在塑性段，材料的屈服由参数σ1，σ2，σ12，σ21，σ13定义。材料失效则由界面失效准则确定。材料参数如表1所示。

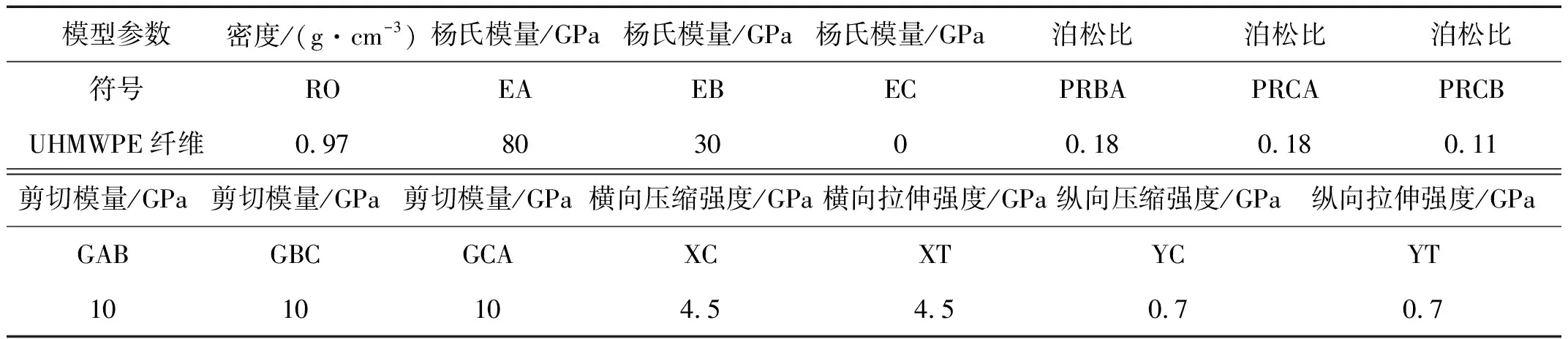
表1 UHMWPE材料力学性能参数

1.2.2 明胶有限元模型

在高速撞击过程中，明胶由于UHMWPE纤维材料变形的挤压和压力波传播的影响，瞬态变形响应主要集中在撞击点区域，表现为明胶的凹陷，成半球状，明胶的其余区域则无明显变形，在对明胶进行网格划分时，同样是撞击点区域密集，而周边较疏，同时，沿着Z轴向，明胶网格不断变疏。其网格示意图如图5，网格数为196 800。

图5 明胶网格示意图

本文采用弹塑性流体动力材料模型(MAT_ELASTIC_PLASTIC_ HYDRO MODEL)和线性多项式状态方程(LINEAR_ POLYNOMIAL STATE EQUATION)描述明胶材料力学性能，明胶材料模型参数如表2所示。

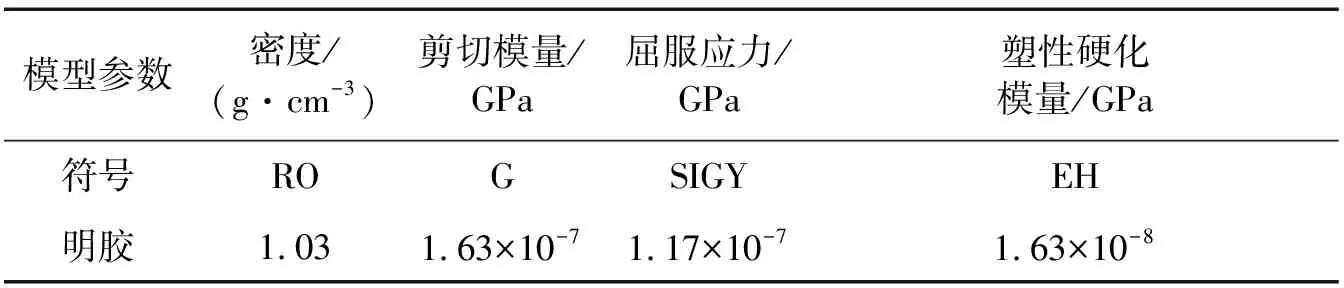
表2 明胶的材料参数

1.2.3 手枪弹有限元模型

手枪弹采用八节点六面体单元(SOLID164)划分网格，网格数为4 272，网格示意图如图6所示。

图6 7.62铅芯弹网格示意图

采用JOHNSON_COOK材料模型和结合GRUNEISEN状态方程来描述手枪弹材料力学性能，材料本构关系如下

σy=(A+BεPN)(1+Clnε*)(1-T*M)

(2)

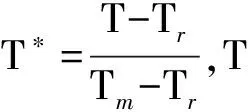
其断裂应变为

(3)

在有限元模型中，手枪弹、软防护及明胶的界面采用面与面侵蚀接触处理(CONTACT_ERODING_SURFACE_TO_SURFACE)。纤维层与层之间的接触采用自动单面接触(CONTACT_AUTOMATIC_SINGLE_SURFACE)，弹丸的铜壳和铅芯两部分的接触选择自动面面接触(CONTACT_AUTOMATIC_SURFACE_TO_SURFACE)。

1.3 实验验证方法

表3 手枪弹Johnson-Cook 材料模型参数

实验系统如图7所示，实验中采用7.62 mm弹道枪发射手枪弹，枪口10 m时, 手枪弹垂直撞击带UHMWPE软质防护的明胶模拟靶标，撞击速度由一套光电测速靶测量。PCB113B22压电传感器被埋设在明胶靶标内(15，15，6)位置，正对撞击点，用于测量明胶内压力。一台高速摄像机被布置在带纤维软防护明胶靶标的侧面，通过拍摄和图像处理来测量软防护和明胶的背凸情况，拍摄速度为40 000帧/秒。

图7 实验系统示意图

2 研究结果与分析

2.1 侵彻与UHMWPE软质防护破坏过程分析

采用LS-DYNA软件对450 m/s速度的7.62铅芯弹高速撞击带UHMWPE软质防护的明胶模拟靶标问题进行了数值计算，计算获得的弹体侵彻与纤维软防护的破坏过程如图8所示，纤维层面Von Mises应力演化变化过程如图9所示，弹丸侵彻软防护过程中速度和加速度变化如图10和11所示。

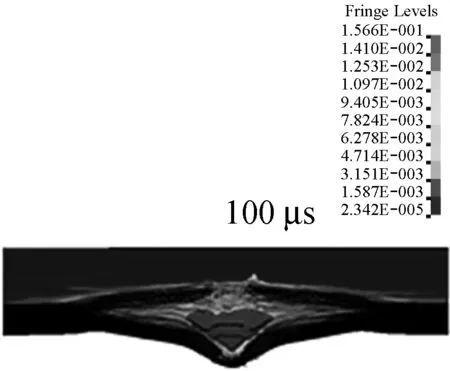
图8 手枪弹撞击时UHMWPE软防护Von Mises应力

图9 纤维层面Von Mises应力演化图

图10 7.62铅芯弹的速度时程图

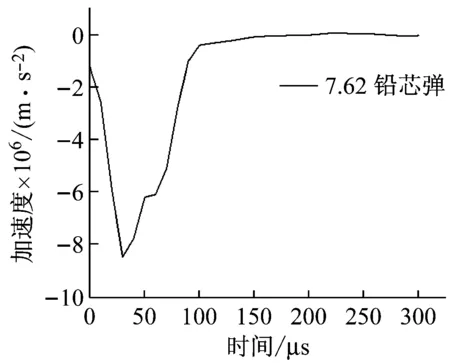
图11 7.62铅芯弹的加速度时程图

高速撞击过程中，7.62铅芯弹速度首先快速下降，然后趋于零。相应地加速度从0～30 μs时期快速上升，而后经历了30～100 μs这一时间段的衰减趋于零。根据7.62铅芯弹速度的衰减过程，可以将7.62铅芯弹侵彻带纤维软防护明胶靶标过程分成三个阶段。

侵彻早期：从7.62铅芯弹开始接触纤维软防护到30 μs，当高速前进的7.62铅芯弹与纤维软防护前面的纤维层接触，由于7.62铅芯弹具有较高的动能，对纤维层产生剪切作用，当纤维承受剪切应力超过极限时，纤维破坏。由于此刻弹丸变形不大，故前面纤维层的破口直径也不大。随后没有贯穿的UHMWPE纤维层被挤压成，应力波在UHMWPE层与层之间传播，并快速传播到纤维软防护的最底层，同时纤维对弹丸产生阻碍作用，导致7.62铅芯弹承受纤维层的阻力急速上升，反向加速度上升最高至8.45×106m/s2，7.62铅芯弹的速度由初始的450 m/s锐减至320 m/s。当弹丸的应力超过它的极限时，弹丸出现镦粗变形。这一阶段防护后面的纤维层由于受到前部纤维层的挤压作用，开始出现一些拉伸变形。

侵彻中期：随着弹丸侵彻的继续，纤维层受剪切和拉伸破坏的纤维束不断增多，前面已经破坏的纤维层不再对弹丸有阻碍作用，且弹丸的速度相比于初始时刻要小很多，弹丸所受的阻力开始下降，加速度由30 μs时的8.45×106m/s2衰减至100 μs时的396 157 m/s2，7.62铅芯弹的速度进一步下降。由于UHMWPE材料的阻力作用，弹丸变形不断增加。此阶段，UHMWPE纤维明显拉伸变形，弹丸的动能一部分转化为自身的变形能，另一部分转化为纤维的弹性势能。当纤维的拉伸超过极限应变时，纤维被拉断。随着弹丸接触面积的不断增大，UHMWPE防护破口直径不断增大。应力场计算结果表明在这一阶段，应力波在纤维层面的传播半径不断增大，并且应力波在到达软防护底层会发生反射现象。

侵彻后期：7.62铅芯弹侵彻速度持续下降，弹丸受到纤维软防护的阻碍作用进一步减小，7.62铅芯弹的反向加速度不断下降并趋于零，弹丸的墩粗现象越发明显，变成伞状，7.62铅芯弹的弹头壳出现破损，动能进一步转化为弹丸自身的变形能和纤维的弹性势能，直到弹丸不再前进。UHMWPE软防护后面出现“背凸”。由于纤维回弹，7.62铅芯弹出现被弹回现象。

图12是高速撞击过程中手枪弹变形和表面等效应力分布，10 μs时，7.62铅芯弹的外壳呈现明显的色彩分层，其中与纤维层最先接触的弹尖部分铜壳应力最大。随着7.62铅芯弹的侵彻深入，弹头壳上的最大应力区域开始后移，开始出现破损，到50 μs时，7.62铅芯弹变成蘑菇形，铅芯开始外露。100 μs时，由于铅材质比较软，加之但头壳比较薄，使得7.62铅芯弹受纤维层的阻碍作用而出现形体后翻现象，整个弹丸呈一伞状。到800 μs时，由于纤维的阻碍作用，铅芯与弹头壳被剥离。

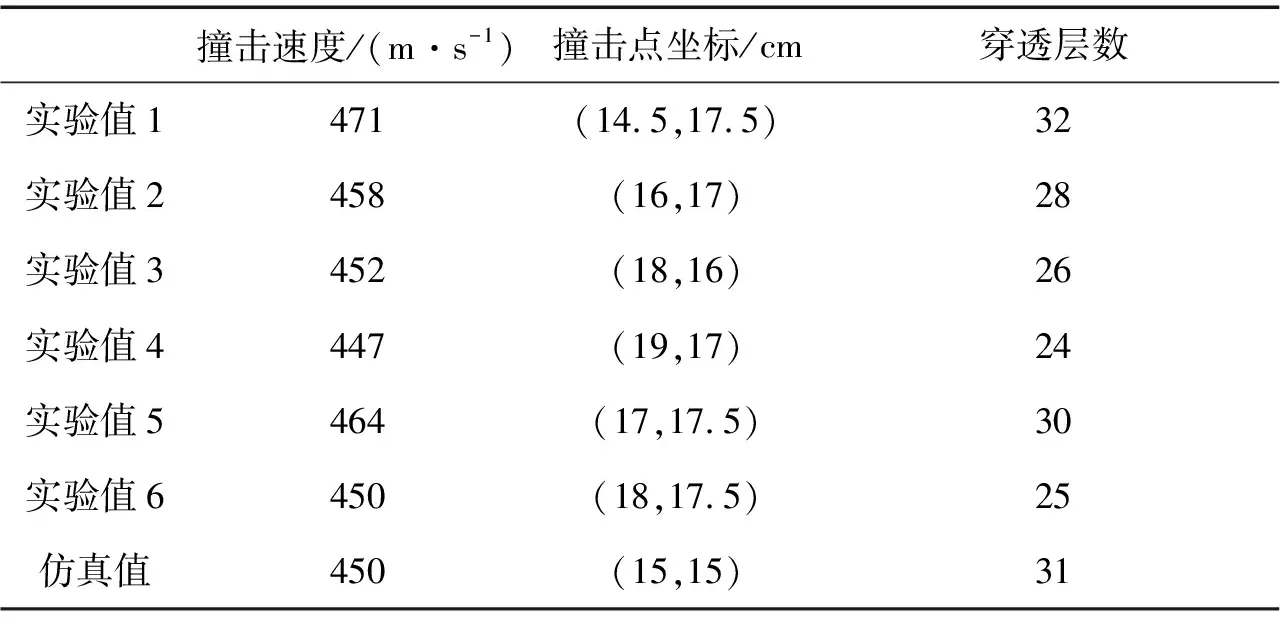
在7.62铅芯弹高速撞击带超高分子量聚乙烯纤维软防护明胶靶标的实验中，共射击6发7.62铅芯弹，实验和数值计算的被破坏的纤维层数对比如表4所示。

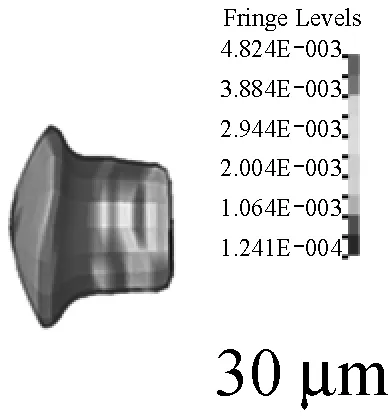
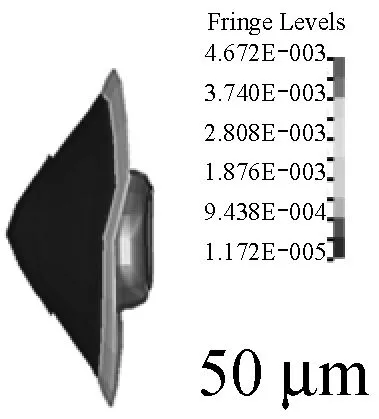
图12 弹体变形与表面Von Mises应力变化

撞击速度/(m·s-1)撞击点坐标/cm穿透层数实验值1471(14.5,17.5)32实验值2458(16,17)28实验值3452(18,16)26实验值4447(19,17)24实验值5464(17,17.5)30实验值6450(18,17.5)25仿真值450(15,15)31

如表4所示，实验中，7.62铅芯弹的撞击速度为447～471 m/s，撞击点较集中在纤维软防护中心点(15，15)周围，纤维层被穿透层数为24层到32层。7.62铅芯弹的撞击速度定为450 m/s，垂直撞击，数值计算获得的穿透纤维层数为31层，计算与实验基本一致。

2.2 明胶靶标瞬时空腔响应分析

计算与实验都发现在高速撞击后期及弹体停止运动后，明胶靶标中出现瞬时空腔效应，图13为0～1 000 μs过程中，数值仿真和实验的明胶瞬时空腔随时间变化对比情况，带UHMWPE软防护的明胶靶标在7.62 mm铅芯弹高速撞击作用下，由于纤维软防护的变形挤压作用，撞击点区域的明胶开始出现凹陷，形成瞬时空腔，形状类似一半球状。随着时间的推移，弹丸侵彻不断深入，软防护的变形加大，同时加上应力波的传播，使得明胶撞击点区域的瞬时空腔半径和深度都不断加大，500 μs时，空腔深度为21.0 mm；1 000 μs时；空腔深度为42.8 mm；计算获得的明胶瞬时空腔膨胀最大速度可达56 m/s。如图13，计算的明胶瞬时空腔变化与实验吻合较好。

图13 数值仿真与实验的明胶空腔对比

从图14的典型时刻明胶中等效应力图可以看出，明胶的等效应力作用区域成一半球状，球心位置为撞击点。最大等效应力层始终处在明胶瞬时空腔边缘区域，沿径向成明显的颜色分层，越远离撞击点，等效应力值越低，在0 μs到1 000 μs时期，明胶瞬时空腔半径和深度随时间的推移而不断加深，凹陷的半球持续膨胀。

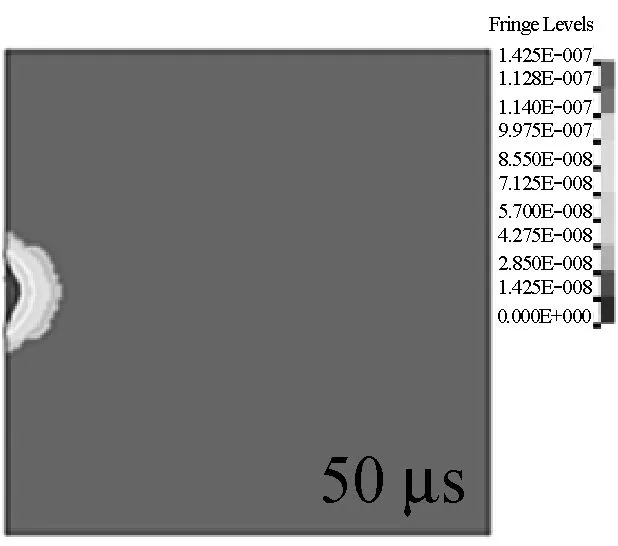
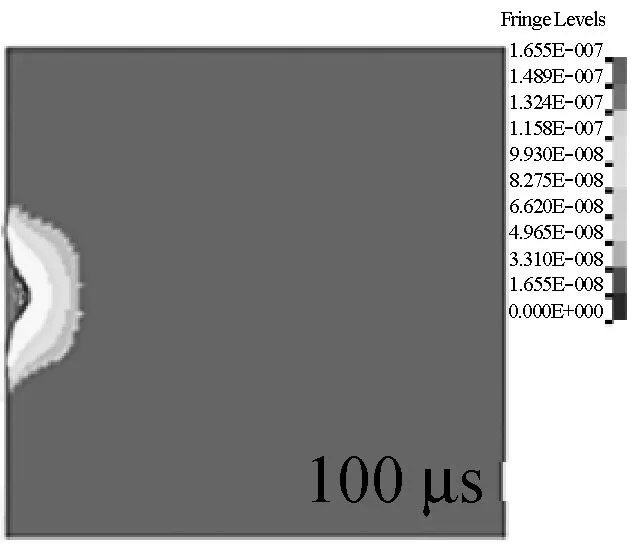
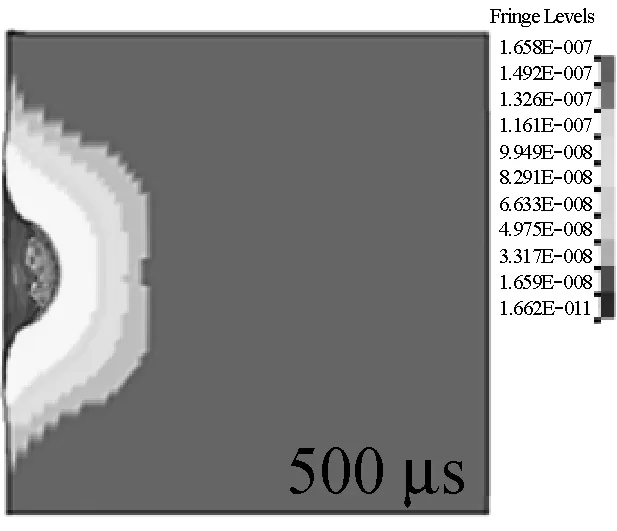
图14 明胶靶标Von Mises应力等效应力变化情况

2.3 明胶靶标压力场分析

计算发现明胶压力场分布与等效应力分布类似，以撞击点为球心波呈半球状。初始时，明胶的撞击点处压力最大，半球的半径较小，而后随着时间的推移，压力波半球半径不断增大，传播速度约为1 500 m/s。而后压力波传播到明胶的边界处，由于边界效应的影响，到达边界的压力波开始反射，并与原先径向的压力波相互干涉。

计算获得的明胶中(15，15，6)点处的压力值曲线如图15所示，由于冲击压力波传播和软防护变形挤压作用，从30 μs开始，明胶压力值快速上升，到70 μs时，最大压力峰值达4.29 MPa。而后由于7.62铅芯弹停止前进，纤维软防护不再继续凹陷变形，开始回弹，对明胶挤压减弱，同时明胶中的压力波继续扩散，压力点的压力值开始衰减，当压力波传到明胶的边界时，压力波开始反射，使得压力点的压力值开始出现多次正负值，即明胶受到反复拉和压作用。

图15 明胶中(15，15，6)点的压力变化

实验验证中，压力传感器的埋设在明胶 (15，15，6)点，各次实验所得埋设点的最大压力峰值如表5所示。

表5实验和数值仿真中明胶压力点压力峰值对比

Tab.5Compressionofmaximumpressureofatypicalpointingelatinbetweenexperimentandnumericalsimulation

撞击速度/(m·s-1)撞击点坐标/cm测量点最大压力值/MPa实验值1471(14.5,17.5)4.55实验值2458(16,17)3.0实验值3452(18,16)2.68实验值4447(19,17)3.41实验值5464(17,17.5)6.0实验值6450(18,17.5)2.84仿真值450(15,15)4.29

从表中可以看出，明胶中压力测量点的最大压力值区间为2.68～6.0 MPa，从表中的撞击点坐标可以看出，7.62铅芯弹高速撞击软防护的撞击点集中在以(15,15)为中心的一定半径区域内，较为集中。数值模拟中，7.62铅芯弹的撞击点坐标选为(15,15)，计算所得明胶中(15,15,6)点处的压力最大值为4.29 MPa，在实验值区间内，与实验较好的吻合。

2.4 能量传递分析

7.62 mm手枪弹高速撞击“带UHMWPE软防护明胶模拟靶标”的过程也是能量转化的过程，计算获得的数值7.62 mm铅芯弹和明胶的能量变化曲线如图16所示。当7.62铅芯弹接触UHMWPE软防护明胶模拟靶标过程中，7.62铅芯弹的能量有一段明显的下降过程，由最初的565 J快速下降到70 μs时的147.7 J，随后能量趋于稳定。对应地明胶的能量在这一过程开始上升，这主要由于纤维软防护的变形和应力波的传播双重作用，明胶撞击点区域聚集变形能而凹陷，从图中可以看出，明胶的能量最大值为111.6 J，7.62铅芯弹的初始能量为565 J，明胶所得的能量仅为弹丸初始总能量的19.75%。因此在明胶靶标前加超高分子量聚乙烯纤维(UHMWPE)软防护，有效地减少了弹丸能量向明胶靶标的传递，有防护效果。

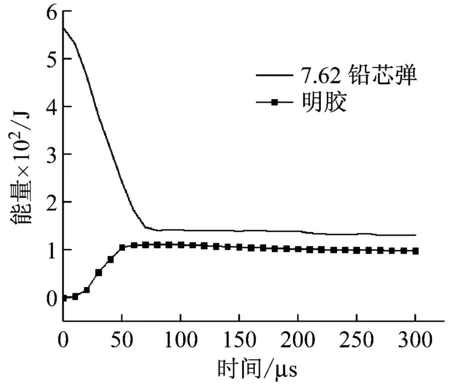
图16 侵彻模型中的能量时程图

3 结 论

(1) 本文建立了7.62典型手枪弹高速撞击“带UHMWPE软防护明胶模拟靶标”非线性有限元计算模型，该模型数值计算结果与实验结果在弹体的变形、软防护的破坏、明胶的凹陷以及明胶中压力点的压力值等方面都吻合较好，验证了模型正确性。

(2) 7.62典型手枪弹侵彻过程中，弹体速度先有一段明显的下降过程，而后归于平缓，而加速度绝对值从0～30 μs区间，快速上升，而后经历了30～100 μs这一时间段的衰减后归零。软防护的等效应力、变形和破坏主要集中在撞击点附近，剪切和拉伸作用是UHMWPE纤维层破坏的主要原因。

(3) 带纤维软防护的明胶靶标受7.62典型手枪弹高速撞击作用后，由于纤维软防护的变形挤压作用，撞击点区域的明胶开始出现凹陷，形成瞬时空腔，形状类似一半球状，该空腔随时间不断变大，最大空腔深度可达42.8 mm。

(4) 7.62典型手枪弹高速撞击带纤维软防护明胶靶标过程中，明胶的等效应力区域成一半球状，球心位置为撞击点，最大等效应力层始终处在明胶凹陷的边缘区域，越远离撞击点，等效应力值越低。压力波成半球状，撞击点为球心，初始时，明胶的撞击点处压力最大，半球的半径较小，而后随着时间的推移，压力波半球半径不断增大。明胶中(15，15，6)位置最大压力值区间为2.68～6.0 MPa。

(5) 7.62典型手枪弹高速撞击带纤维软防护明胶模拟靶标过程中，UHMWPE软防护吸收了大部分能量，而传给明胶的能量较小，仅为弹体入射能量的19.75%, 超高分子量聚乙烯纤维软防护的防御作用明显。