巷道内I型及I/II复合型裂纹在冲击载荷作用下的断裂行为分析

周 磊， 朱哲明， 应 鹏， 王 雄， 王 蒙

(四川大学 建筑与环境学院，深地科学与工程教育部重点实验室，成都 610065)

巷道在钻爆法开挖过程中，围岩受到爆炸载荷作用产生新的裂纹或者诱发天然裂纹的发育，裂纹缺陷的存在极大地影响着巷道结构的稳定性。在煤矿开采的过程中，冲击载荷是巷道典型的动力灾害之一，掘进爆破、顶板破裂、工作面来压等都可能带来瞬时冲击作用，在冲击载荷作用下，可能导致岩体的局部失稳，以突然、急剧猛烈的形式释放弹塑性变形能，导致岩体的瞬时严重破坏，并伴随大量煤岩粉突出。这种动力灾害在煤炭开采中较为普遍，一般都会产生灾难性的后果[1]。因此煤矿巷道动力灾害研究一直是国内外研究的重点之一。

Everitt等[2-4]探究了地下空间结构、煤矿开采巷道损伤区域的形成机制和范围。刘永胜等[5]研究了爆破作用下隧道含裂隙围岩的开裂机理和破裂范围，并定量分析了爆破作用对隧道松动圈形成过程的影响。潘一山等[6]利用爆炸加载相似模拟试验和数字散斑观测方法(DSCM)研究了高速冲击载荷作用下巷道的动态破坏过程。孔德森等[7-8]利用 LS-DYNA 动力分析软件，采用流固耦合算法数值模拟了爆炸荷载作用下地铁隧道的冲击反应。

对于含裂隙缺陷的岩体，裂纹的动态断裂韧度是确定裂纹对岩土体动态稳定性的重要指标。众多的国内外学者针对岩石等脆性材料的静态与动态断裂韧度进行了较多的研究。Zhu等[9-11]采用物理模型试验研究了含裂纹巷道与无裂纹隧道的稳定性具有较大的差异，并指出裂纹尖端的应力强度因子是巷道整体强度评价的重要参数。Wang 等[12-14]采用分离式霍普金森压杆(SHPB)对大尺寸压缩单裂纹圆孔板试样结合应变片进行了I/II复合型裂纹动态断裂韧度的测试，指出试验-数值法对于裂纹动态扩展韧度的计算具有较好的可行性。Zhang等[15-16]采用SHPB装置结合准静态方法测试了三点弯曲巴西半圆盘试样的动态断裂韧度，指出数字图像相关法目前在岩石类脆性材料方面仅局限于准静态试验研究。Wang等[17-19]采用应变片测试了侧开单裂纹半孔板试样的动态断裂韧度，并对I型及I/II复合型裂纹扩展特性进行了数值分析。

对于岩石材料的动态断裂行为研究，主要分为数值分析和试验手段，而把两种方法相结合处理是一种较为合理以及较多的研究方式。在数值模拟方面，AUTODYN为一款基于动态有限差分法的数值分析软件，该软件能够分析岩石类几何非线性和材料非线性的动力学断裂问题，已经被众多的国内外研究学者应用于脆性材料在爆炸和冲击荷载下的课题研究[20-22]。对于ABAQUS有限元分析软件进行裂纹动态应力强度因子计算，解德[23]采用ABAQUS数值计算了无限大板中心裂纹的动态应力强度因子时程曲线，并与有限差分法的解析解进行了对比分析，验证了该计算方法的有效性。相对于试验手段而言，随着霍普金森压杆试验装置的发展与进步，大直径分离式SHPB装置可方便地实现实验室内对岩石类等非均质脆性材料试样高速加载，并且已经在各个研究领域都有较为成熟的研究，越来越多的研究学者采用该试验装置进行脆性材料的动态断裂试验的研究，但SHPB试验装置杆件直径相对于巷道模型试样尺寸较小，试验数据处理较为繁琐等问题还是一直存在[24]。

目前对于巷道内裂纹在冲击载荷作用下的研究尚处于初步阶段，特别是巷道内I/II复合型裂纹在冲击载荷作用下动态断裂问题的研究寥寥无几。本文基于SHPB试验装置原理以及断裂力学和冲击动力学的基础上，以可调速落锤冲击试验机作为冲击加载装置进行裂纹巷道模型试样的动态加载试验，采用应变片对裂纹的起裂时间及扩展时间进行监测，并借助于ABAQUS和AUTODYN软件数值分析巷道围岩内裂纹的扩展特性，对巷道内裂纹的起裂韧度等断裂参数进行计算，为巷道工程理论实践提供一定的理论指导意义。

1 巷道模型制作及试验方法

1.1 模型试样及材料的选择

假设某煤矿开采巷道的高度为6 m，宽度为5 m，圆拱半径为2.5 m，以此实际工程巷道尺寸按100∶1的比例进行缩小设置，巷道高度h=60 mm，宽度w=50 mm，圆拱半径r=50 mm。巷道模型试样大小为350 mm×300 mm×30 mm，底板高度L=90 mm，如图1(a)所示。巷道模型尺寸经过准静态试验的论证，能够充分地表观巷道模型在静态载荷作用下的断裂行为[25-26]，这也是本文选择此巷道模型尺寸的重要依据之一。在巷道钻爆法掘进过程中，拱顶圆弧围岩区域会产生各种径向裂纹，为了让本文研究更接近于实际工程概况，因此将单裂纹设置于拱顶圆弧区域，裂纹长度l=50 mm，与拱顶圆心的距离比为α=d/r，α=0～1。

巷道模型试样材料选用隆昌青砂岩，该砂岩材料动态力学性质参数泊松比νd=0.21，弹性模量Ed=12.5 GPa，密度为ρ=2 265 kg/m3，纵波波速cd=2 492.46 m/s，横波波速cs=1 510.12 m/s，瑞雷波波速cR=1 378.3 m/s。裂纹采用0.5 mm厚的拉花锯条进行加工处理，随后裂纹尖端采用0.1 mm厚的美工刀片进行锐化处理，使得裂纹尖端的应力集中现象更为精确，如图1(b)所示。巷道内裂纹与拱顶圆心的距离比α以0.25为梯度增量制作5组模型试样，α分别为0、0.25、0.5、0.75、1。为了避免动态冲击试验的偶然误差等因素对试验结果的影响，选择每组制作5个巷道模型试样，总共制作25个试样。

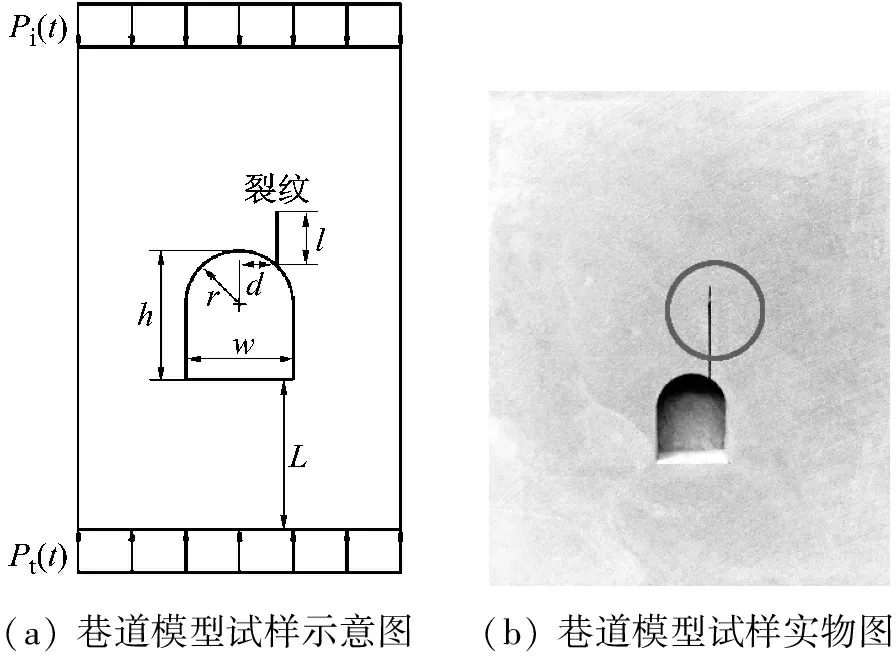
(a) 巷道模型试样示意图(b) 巷道模型试样实物图

图1 巷道模型尺寸示意图

Fig.1 Sketch map of tunnel model

根据裂纹尖端的应力场和位移场的演化，引入应力强度因子KI、KII、KIII概念，大部分研究性课题主要针对KI、KII对结构稳定性的影响进行研究。为了验证裂纹的距离比α对巷道内裂纹断裂模式的影响，本文采用ABAQUS进行裂纹巷道模型的构型验证，裂纹尖端的应力强度因子KI、KII随裂纹距离比α的变化如图2所示。从图中可以看出，当裂纹α=0时，KII/KI=0，表明KII值很小，该巷道模型试样预制裂纹为纯I型裂纹。当α>0时，KII/KI先增大后减小，说明当裂纹偏移巷道对称轴距离越大时，II型裂纹的应力强度因子对巷道的稳定性影响先增大后减小，但相对于α=0时，KII的相对影响还是较大。

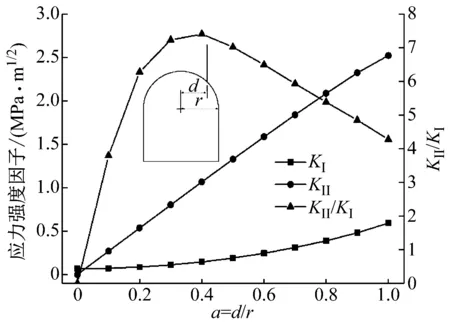
图2 预制裂纹尖端应力强度因子随距离比α的变化

1.2 动态加载设备

冲击加载装置以自行研制的能实现中低冲击加载速度的可调速落锤冲击试验机进行加载，冲击杆件的材料选用 LY12CZ铝合金，该材料的弹性模量为71.7 GPa，泊松比为0.3，密度为2 850 kg/m3。基于一维应力波传播的假设，弹性入射波在入射杆中以波速c0=5 860.78 m/s，实测波速cb=5 936.73 m/s。入射杆长度li=3 000 mm，透射杆长度lt=2 000 mm，冲击落锤高度300 mm。入射杆上贴有3张应变片，入射杆上的应变片SGi到试样上端面的距离分别为l1=350 mm，l2=1 500 mm，l3=2 650 mm，透射杆上的应变片SGt距离试样下端面的距离lt=450 mm，冲击加载装置工作原理如图3所示。落锤下落冲击加载速度由光电测速装置进行测量，加载波形为半正弦波，同时采用超动态应变采集仪和应变片测试系统，实时观测记录试样的动力响应特征和裂纹扩展特性。应变信号由超动态应变仪进行信号放大后由高频示波器采集，最后经过试验数据处理系统进行后期处理，得到入射杆与透射杆的应力加载波形。

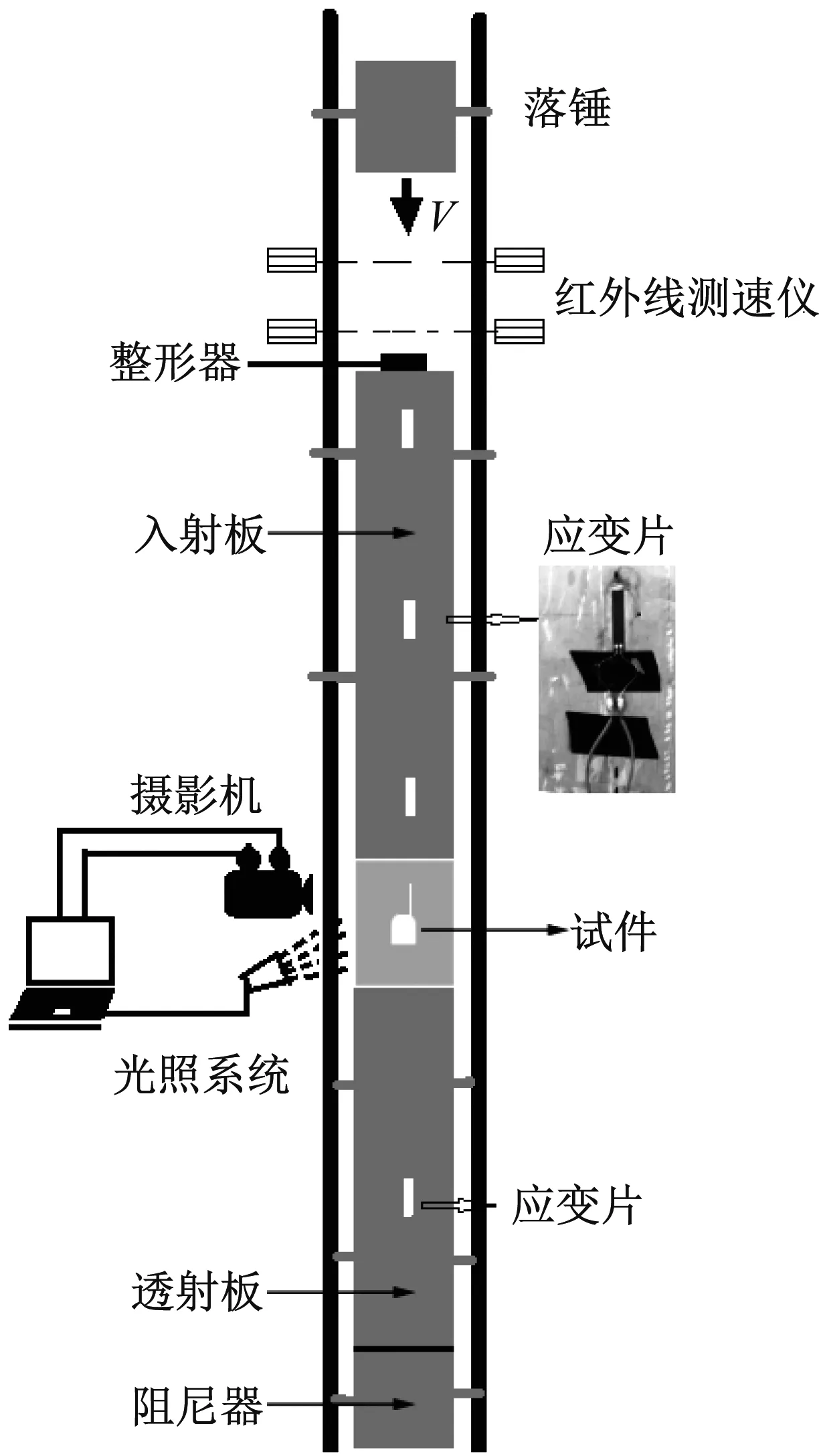
图3 冲击加载装置

为了有效延长加载波形上升沿并且降低波形中包含的高频振荡成分，同时为了减小波形弥散效应和惯性效应，在落锤与入射端之间粘贴黄铜片作为波形整形器，可以获得理想的加载波形使试验过程更接近SHPB一维应力波假设[27]。为了避免巷道模型试样上下端面摩擦效应对试验数据的影响，在模型试件加载上下端面涂抹少量黄油，并采用木质夹具平整的夹持于入射杆与透射杆之间。

1.3 试验数据

在落锤冲击试验过程中，入射杆和透射杆中的脉冲信号通常采用贴在杆件上的应变片进行测量。当应力脉冲在杆件中传播时，应变片感应脉冲信号并传输至应变仪进行记录。由高速示波器采集得到(α=0.5)试样No.2的入射杆上的入射应变和反射应变及透射杆上的透射应变的典型电压信号如图 4所示。从图中可以看出，该冲击试验装置能够很好的测试入射杆与透射杆的应变信号时程曲线，且与SHPB试验装置基本一致，表明该试验装置能够很好的实现岩石等脆性材料在中低速冲击载荷作用下的动态试验[28]。

为了更好监测裂纹的扩展路径，在裂纹的扩展路径中粘贴两张应变片，分别记为SG1和SG2，如图5所示。当裂纹起裂时导致应变片SG1被拉断，电压信号形成突变，对电压信号进行求导，在导数的极值时刻即为应变片的断裂时刻，也即为裂纹的起裂时间ti。同理，当裂纹扩展至应变片SG2时，SG2被拉断的扩展时刻tp，就可以得到SG1与SG2的断裂时刻分别为ti和tp，从巷道内裂纹的起裂时刻ti和扩展时刻tp进一步通过试验-数值法能够确定裂纹的起裂韧度等断裂参数。

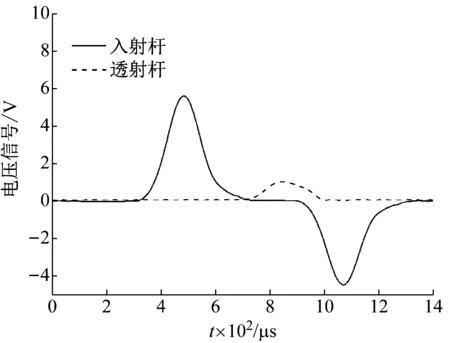
图4 入射杆与透射杆典型的电压信号

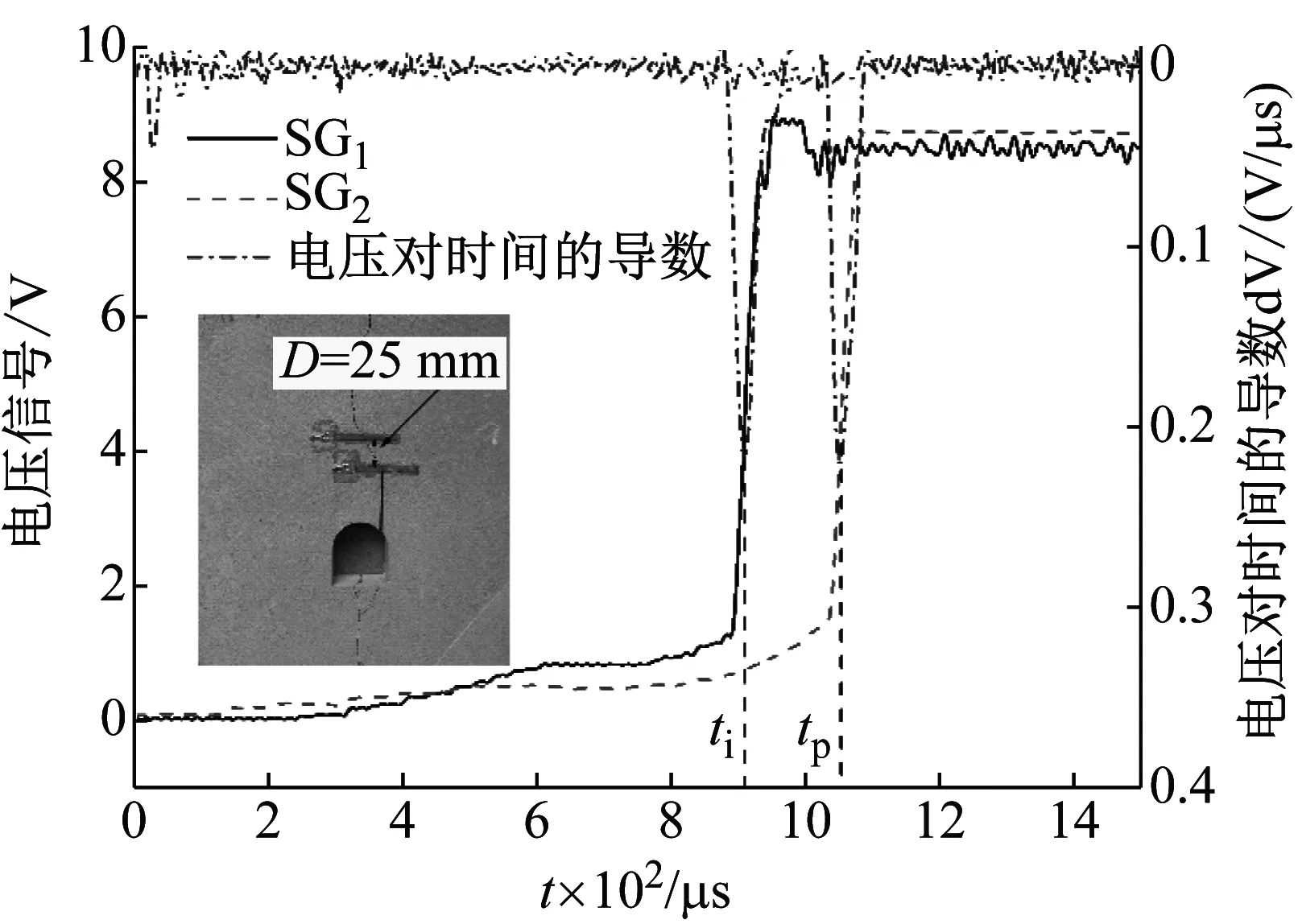
图5 巷道模型试样上应变片的电压信号

根据一维应力波理论，入射杆施加在巷道模型试样上端面的动态载荷Pi(t)可以通过入射波和反射波叠加得到。透射杆施加在巷道模型试样下端面的动态载荷Pt(t)可以由透射杆上监测到的透射波得到，其计算公式如下

(1)

式中：Ed为弹性杆件的动态弹性模量；As为巷道模型试样的加载截面面积；εi，εr分别为入射杆上的入射应变时间历程和反射应变时间历程，εt为透射杆上透射应变时间历程。

由于本文的研究方法为试验-数值法，已经不在准静态法研究的范围之内，因此不用满足准静态法研究中的应力平衡假设，故选择巷道模型试样所受载荷Pi(t)作为动态试验的加载载荷。根据式(1)进行入射波与反射波的叠加，叠加后的载荷波形如图6所示。以巷道模型试样入射上端面受到应力波加载为起点时刻to，并设为随后所有时刻为相对时刻，由此可以得到(α=0.5)No.2试样内预制裂纹的相对起裂时刻ts=ti-to=466 μs，相对扩展时刻ta=tp-to=612 μs。图中Pmax=218.36 kN为巷道模型试样(α=0.5)No.2的最大荷载值，tpmax=247 μs为最大载荷值所对应的相对时刻，同理可得到每组试件的起裂时间与扩展时间等试验数据，统计于表1中。

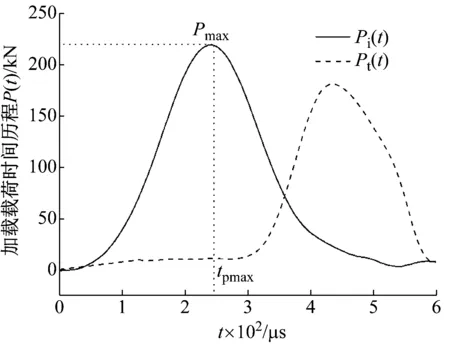
图6 巷道试样(α=0.5)No.2入射端和透射端的加载波形

2 动态断裂参数测试

岩石动态断裂韧度是评价岩土体抵抗裂纹动态起裂和扩展性能的重要阀值，不仅是岩石断裂动力学的基本力学参数之一，也是岩土体强度质量评价的重要指标[29]。本文采用J积分算法计算巷道模型试样中裂纹的动态应力强度因子，将试验测得的动态载荷时程曲线Pi(t)代入有限元程序ABAQUS中，得到裂纹尖端的动态应力强度因子时程曲线，结合试验时记录的巷道模型试样起裂时刻ts便能确定对应试样的动态起裂韧度，这种方法已经被众多国内外研究学者应用于动态试验研究。

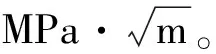
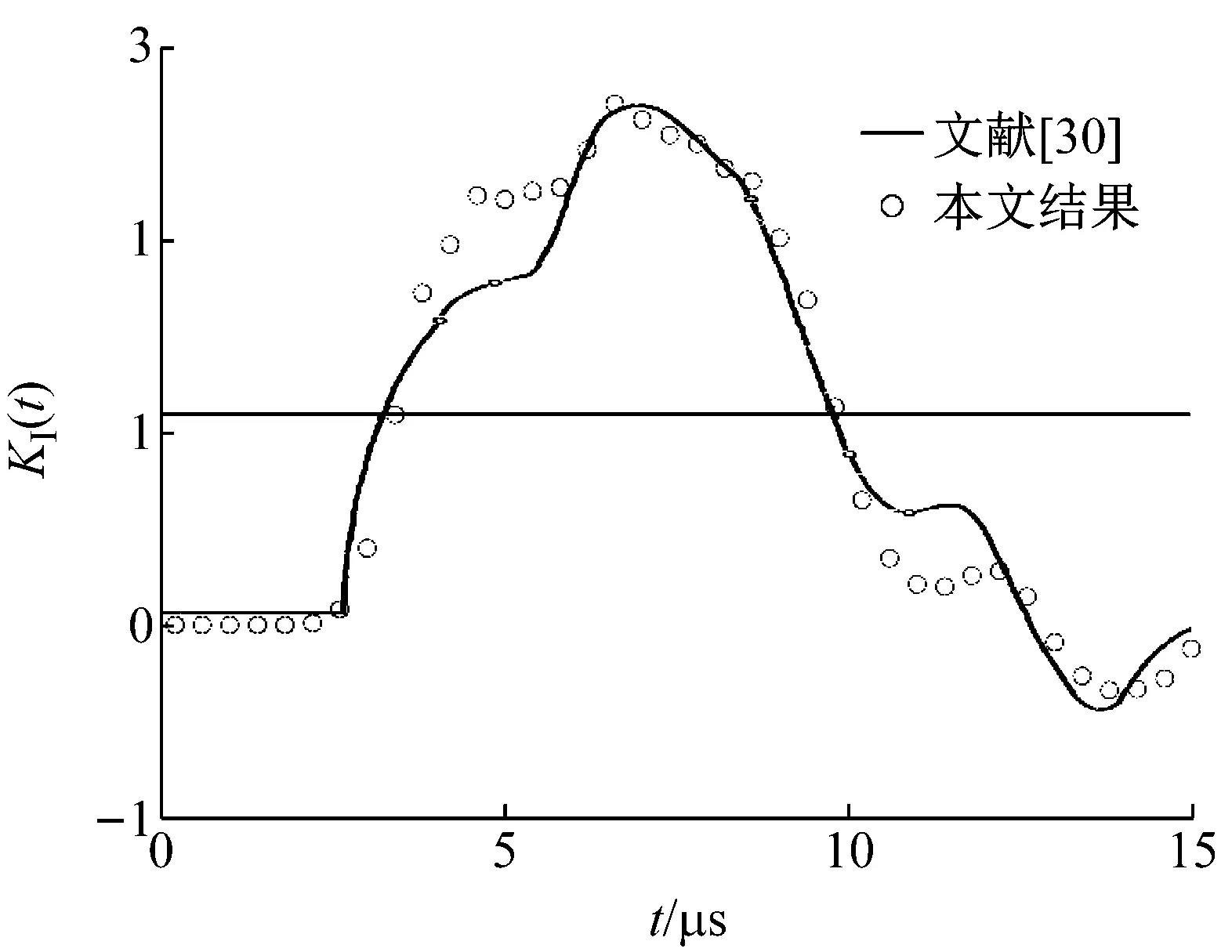
图7 本文有限元计算结果与Chen和Wilkins[30]计算结果对比

Fig.7 Comparison between the results of finite element ABAQUS code and those of Chen and Wilkins

2.1 普适函数的应用

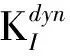
(2)

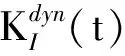
关于动态断裂的进一步研究中，Ravi-Chandar指出，裂纹扩展速度v的普适函数值k(v)可由如下近似公式计算[32]

(3)

式中：cd为材料的纵波波速；cR为材料的瑞雷波波速。从式(3)中可以看出，k(v)为关于裂纹扩展速度v的减函数，当试样受到动态载荷但裂纹未起裂时v=0 m/s，此时k(v=0)=1。即

(4)

通过此种方法就可以获取巷道模型试样裂纹未起裂时的I型动态应力强度因子时程曲线，随后结合试验数据所测得裂纹起裂时间ts，就可以确定I型裂纹的起裂韧度参数。而对于巷道模型试样内II型动态应力强度因子时程曲线结合起裂时间ts获取裂纹尖端的II型裂纹的起裂韧度参数。

2.2 动态起裂韧度的确定

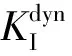
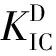
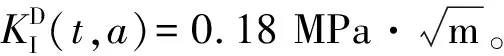
从准静态方法与试验-数值方法对比可以看出，两者所测的动态起裂韧度相对误差较大。准静态法认为巷道模型试样在受到最大载荷Pmax时刻tpmax作为预制裂纹的起裂时刻。但是动态冲击试验经过应变片所测的裂纹实际的起裂时刻ts远落后于tpmax，这种滞后现象是由于动态加载的惯性效应所导致的。由应变片SG1所测的裂纹实际的起裂时刻ts，准静态方法计算的动态应力强度因子时程曲线已经开始呈下降趋势，而试验-数值法所得到的动态应力强度因子时程曲线在试样起裂前随着时间的增加呈递增的趋势，在起裂时刻ts处所得的动态起裂韧度是巷道模型内裂纹开始起裂时刻。经过两者方法的对比分析可知，试验-数值法计算得到的动态起裂韧度更符合动态冲击试验的测试情况。

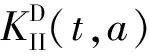
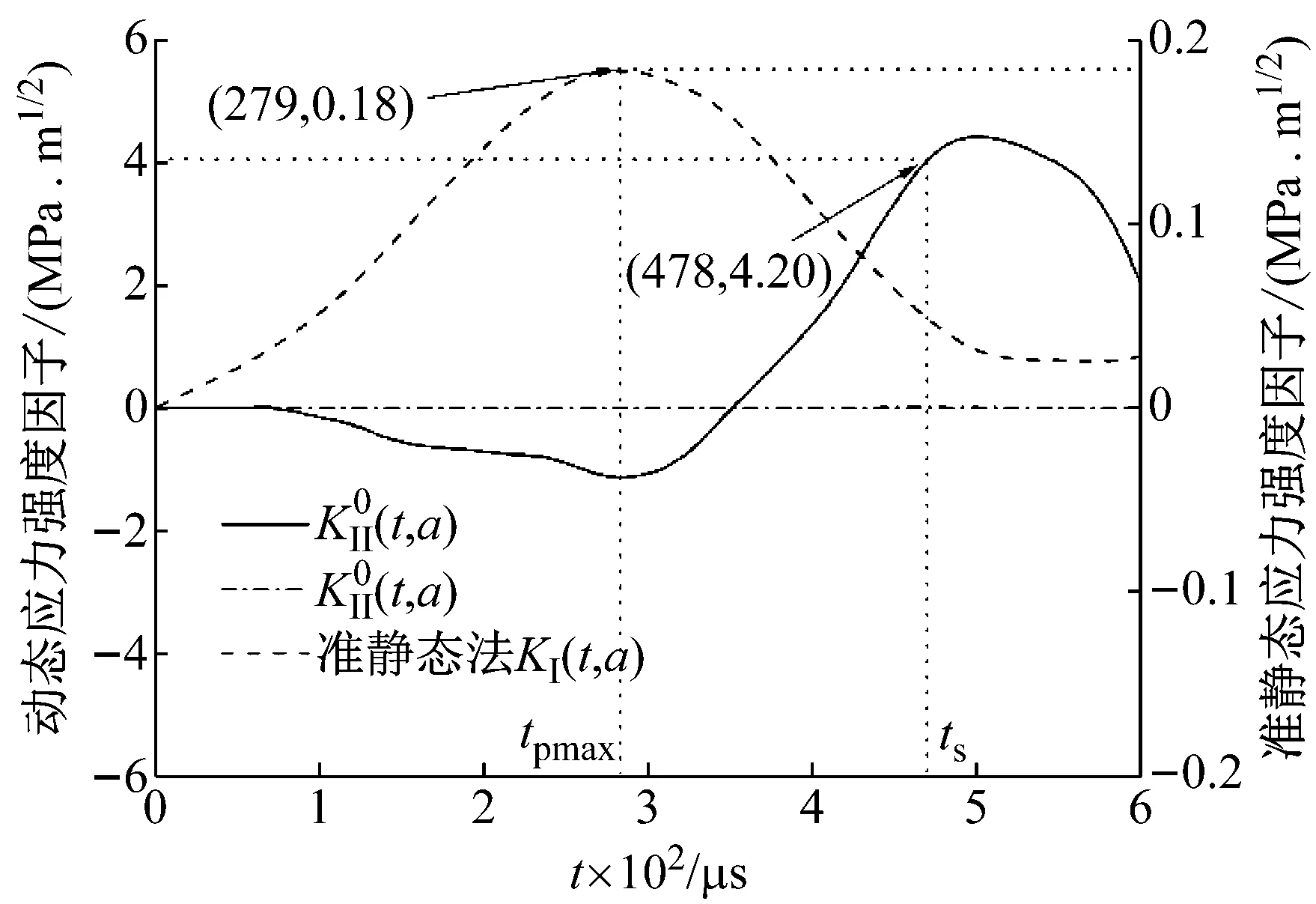
图8 α=0巷道模型试样预制裂纹初始开裂前的应力强度因子演化

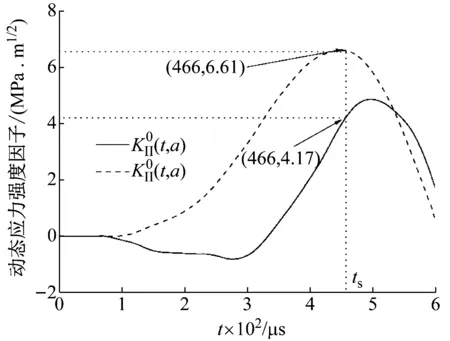
图9 α=0.5巷道模型试样预制裂纹初始开裂前的应力强度因子演化

根据不同距离比α得到每组巷道模型试件裂纹起裂时的动态断裂韧度，如表1所示。

3 数值分析

为了研究巷道内预制裂纹在动荷载作用下的扩展特性，本文采用有限差分法AUTODYN软件进行数值模拟，研究在冲击载荷作用下裂纹的扩展路径。基于图1(a)的巷道模型尺寸，建立相应的纯I型和I/II复合型裂纹巷道数值模型，数值模型为三维有限元模型，采用楔形单元进行网格划分，共有237 900个单元。

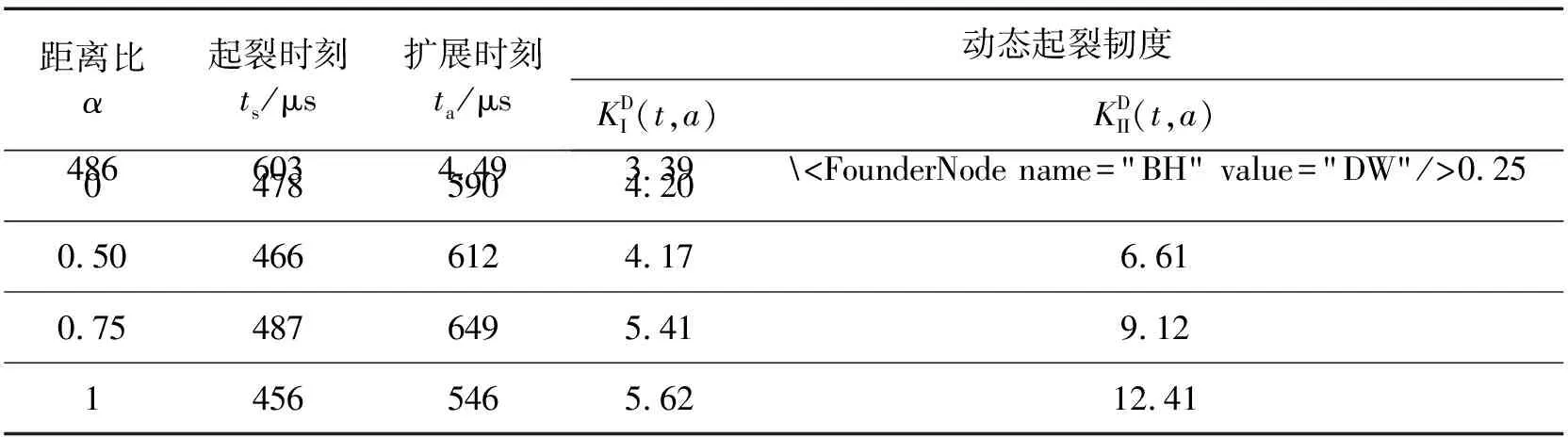
表1 不同裂纹距离比α时的动态断裂韧度

青砂岩材料采用线性状态方程(EOS)，强度模型采用 Elastic。选用的本构模型关系必须具有足够的强度要求和开裂参数要求，因此采用修正的最大主应力破坏准则(MMTS)来作为岩样的失效准则，即当一个细观单元的最大主应力超过材料的最大拉伸强度时，这个细观单元将失效破坏。巷道围岩属于脆性材料，内部本身存在较多的微观裂隙，在动荷载作用下聚集、扩展，最终产生巷道表面宏观裂纹，导致巷道的失稳破坏。因此，在选用最大主应力准则的同时结合拉伸断裂软化损伤破坏模型(Crack Softening，CS)来描述巷道围岩的破坏行为。为了达到与试验相同的加载条件，巷道模型试样加载载荷输入从入射杆与透射杆采集得到的如图6所示的加载波形来进行加载，并在透射杆末端设置一段较长的混凝土传输边界，这样能够防止透射端边界被反射波影响巷道模型裂纹的扩展轨迹。数值分析中传输边界将波的法向分量进行处理，使其达到无反射条件。数值模型参数根据上节1.1中的砂岩参数进行设置。

根据数值分析结果选择α=0、α=0.5、α=0.75这三组数值模型与试验破坏照片进行对比分析，分析不同裂纹距离比α对于裂纹扩展特性的影响，如图10所示。从图中对比可以看出，当α=0时，此时裂纹为纯I型裂纹，裂纹的起裂与扩展方向沿裂纹原方向竖直向上扩展，纯I型裂纹扩展过程中无明显的拐点特征，这与试验结果较为吻合。当α=0.5、0.75时，I/II复合型裂纹起裂与原裂纹形成一定的夹角，形成翼型裂纹扩展，最后沿着巷道的对称轴区域进行扩展，并且复合型裂纹在扩展过程中，存在明显的拐点特征。这也与试验破坏结果较为吻合，表明不同的距离比α会导致复合裂纹的扩展特性不同。根据裂纹的不同距离比α的分布规律，能够很好的判断预制裂纹扩展趋势，如果能够很好的在扩展趋势路径中设置满足止裂条件的止裂构件，这将极大地增强巷道结构在动荷载作用下的动态稳定性。

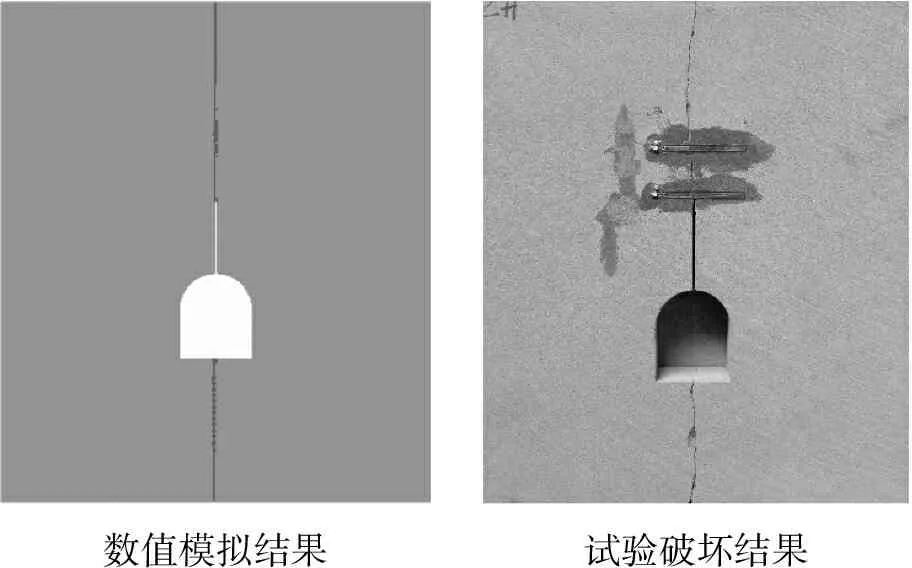
数值模拟结果试验破坏结果

(a) α=0

(b) α=0.5

(c)α=0.75

图10 数值模拟与试验结果对比分析

Fig.10 Comparison between numerical simulation results and experimental results

4 结 论

(1)采用应变片测试巷道模型预制裂纹的起裂时间具有较好的可行性，并结合裂纹的起裂时间能够很好确定裂纹的动态起裂韧度。

(2)本文采用AUTODYN有限差分法软件对巷道内预制裂纹扩展行为进行数值分析，数值结果与试验结果较为吻合，说明AUTODYN能够较好的模拟冲击载荷作用下巷道模型的破坏行为，为巷道工程在动荷载作用下的数值分析提供很好的平台。

(3)通过试验-数值法与准静态法的对比可知，测定巷道模型内预制裂纹的动态起裂韧度时，试验-数值法考虑了岩石材料冲击加载过程中的惯性效应，从计算原理上讲，试验-数值法能够更合理的测试巷道模型的动态起裂韧度，也更符合实际试验情况。

(4)对于巷道内纯I型裂纹的起裂会沿着裂纹的原方向起裂与扩展，而I/II复合型裂纹的扩展会偏向于巷道模型的最大主应力区扩展，即沿着巷道对称轴区域进行起裂与扩展，并在扩展过程中伴随着拐点特征的发生。如果能够在巷道的对称轴区域即最大主应力区域设置满足条件的止裂构件，这将极大地消除裂纹快速扩展的可能性，增强巷道结构的动态稳定性，例如飞机结构中的止裂带等。