短轨枕区间钢轨波磨的现场测试和数值研究

崔晓璐， 闫 硕， 陈光雄

(1.重庆交通大学 机电与车辆工程学院，重庆 400074; 2.西南交通大学 机械工程学院，四川 610031)

随着我国城市轨道交通建设的不断发展，许多城市的地铁线路发展迅速。然而与此同时，各个城市的地铁线路上均出现了不同程度的波磨。根据现场调研发现，钢轨波磨通常发生在小半径曲线轨道的里轨上。当曲线半径R≤350 m，则几乎百分之百发生钢轨波磨。而当曲线半径R≥650～800 m时，则很少发生钢轨波磨。

迄今为止，许多学者均对该现象进行了相关研究[1-2]，主要的研究方法包括现场测试[3-4]，实验验证[5-7]和仿真模拟[8-10]。然而由于钢轨波磨的形成机理十分复杂，至今尚未完全得到解决。根据相关研究综述可知[11]，波磨的总体机理主要包括波长固定机理和损伤机理，这两种机理构成的回馈循环加剧了波磨的形成与发展。其中，损伤机理的主要表现为轨道的磨损，而波长固定机理则反映了轮轨系统的动态行为。对于波长固定机理，目前提出了许多观点来解释地铁线路上的不同波磨现象，其主流观点包括轮轨间瞬态动力学引起振动，P2共振，pinned-pinned共振，轮对弯曲共振，轮轨系统自激振动等。其中，由于轮轨间瞬时动力学引起振动的观点被广为接受，该观点假设钢轨表面在制造和铺设的过程中是不平顺的，这种接触表面的不平顺会引起车轮与钢轨间接触力的变化，从而产生钢轨波磨[12-15]。同时，轮轨系统自身失稳产生不稳定振动导致波磨的观点也常被用来探索波磨形成的潜在机理[16-17]。现有的机理可以用来解释一些波磨现象，但仍有一些不能进行较为合理的解释。为了进一步研究地铁线路上钢轨波磨和轮轨间动态特性的关系，本文基于轮轨摩擦自激振动导致钢轨波磨的观点分别采用现场测试和数值仿真的方法对短轨枕整体道床支撑小半径曲线轨道上的波磨进行了研究。该观点认为[18-20]，当车辆通过小半径曲线轨道时，轮轨间蠕滑力通常趋于饱和。当轮轨间蠕滑力饱和时，轮轨系统可能会产生摩擦自激振动，从而导致钢轨波磨。该观点可以对目前地铁线路上的普遍现象进行较为合理的解释。在现场调研中，测得了波磨严重区间各测点的振动信号。在数值仿真中，建立了较为完整的短轨枕整体道床小半径曲线轨道上的轮轨系统弹性振动模型。采用瞬时动态分析和复特征值分析分别研究了轮对通过时轮轨间的动态特性和不稳定振动模态。综合对比现场测试和数值仿真的结果，可以进一步研究验证钢轨波磨的形成机理。

1 现场测试和数值仿真方法

1.1 轨道现场测点位置

在现场测试中，测点主要布置在距离车站150 m里轨的波磨跟踪测试点处，该区段的曲线半径为350 m，铺设短轨枕整体道床。在该测试点处发现，曲线里轨上出现了明显的钢轨波磨，其显著波长约为125 mm。垂向和横向加速度传感器分别安装在曲线里外轨轨枕上方的轨头外侧、前后两轨枕跨中位置的轨头外侧，以及曲线里外轨的轨枕上，如图1所示。

1.2 仿真模型和数值理论

图2为短轨枕整体道床区间小半径曲线轨道上轮轨系统的结构示意图。由于在短轨枕整体道床中，短轨枕直接嵌入在轨道板内，并固结在一起，它们之间几乎没有任何减振缓冲效果，因此此处将轨枕和道床板作为整体研究。可以发现外侧车轮与外轨的接触点位于车轮轮缘与轨头侧面之间，接触角为δL。而内侧车轮与里轨的接触点则位于车轮踏面与轨头之间，接触角为δR。由于该小半径曲线轨道距离站台较近，经测量该区段的列车速度约为37 km/h。在Simpack中建立了常规客车的整车简化模型，通过模拟仿真可知，当车辆以37 km/h的速度通过半径为350 m的曲线轨道时，轮对两端的垂向悬挂力分别为FSVL=36.5 kN和FSVR=33.4 kN，横向悬挂力分别为FSLL=5.3 kN和FSLR=5.0 kN。并且通过Simpack的仿真结果可以进一步验证在小半径曲线轨道上导向轮对左右轮上的蠕滑力趋于饱和。这意味着其左右轮轨接触点都有明显的滑动速度，此时车轮在钢轨上处于滚滑状态。

(a) 曲线外轨(b) 曲线里轨

图1 短轨枕轨道加速度传感器安装位置

Fig.1 Mounting positions of the acceleration sensors on the track supported by fixed dual short sleepers

图2 短轨枕整体道床区间小半径曲线轨道轮轨系统的结构示意图

Fig.2 Structure diagram of the wheelset-track system on a tight curved track in the fixed dual short sleeper section

根据图2中短轨枕整体道床区间小半径曲线轨道轮轨系统的结构特性，利用Abaqus分别建立了短轨枕整体道床支撑小半径曲线轨道的轮轨系统有限元模型，如图3所示。该模型较为全面地考虑了导向轮对、钢轨、扣件、道床的影响，其材料参数设置如表1所示。轮对为地铁中常用的直径为840 mm的磨耗型踏面轮对，使用该踏面的轮轨很少出现两点接触现象，因此在本文中不予考虑。在车轮与钢轨的接触部分，进行了网格细化，其间的摩擦因数设为0.4。轨道曲线半径为350 m，轨距为1 435 mm。由于建立模型时采用了平行于钢轨的局部坐标系，因此轨底坡和外轨超高的影响可以忽略。钢轨型号为60 kg/m，其两端采用固定约束。在钢轨与轨枕之间，采用DTVI2扣件连接，扣件间距为625 mm，该扣件通过弹簧和阻尼单元模拟。由于钢轨底部与轨枕顶部的节点是两两对应，扣件的刚度和阻尼采用Python脚本平均分配到每一个节点对上。其刚度和阻尼参数通过实验测试和相关参考文献获得[21-22]，垂向刚度和阻尼分别为KRV=40.73 MN/mm和CRV=9 898.70 Ns/m，而横向刚度和阻尼分别为KRL=8.79 MN/mm和CRL=1 927.96 Ns/m。路基的支撑刚度和阻尼为Kf=1.7×105kN/m和Cf=3.1×104Ns/m。

(a) 模型概述

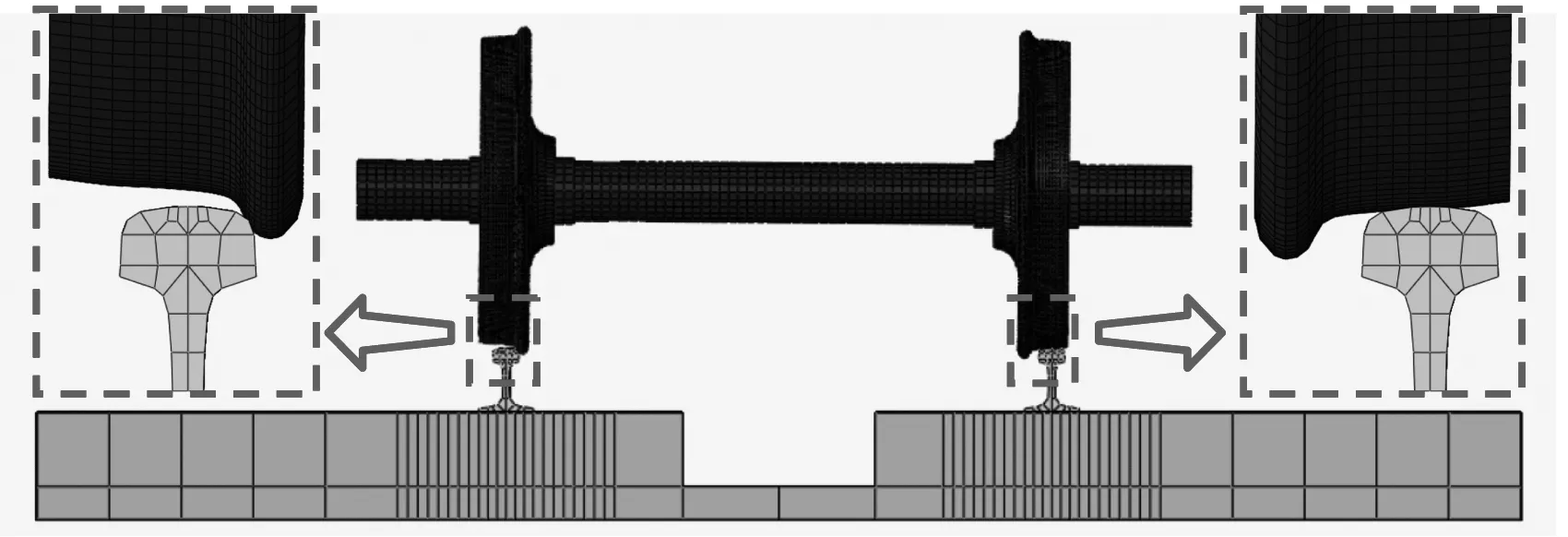
(b) 轮轨接触细节

部件密度/(kg·m-3)弹性模量/Pa泊松比轮对7 8002.1×10110.3钢轨7 7902.059×10110.3道床2 4003.25×10110.24

在本文中，主要对轮轨系统仿真模型进行了瞬时动态分析。瞬时动态分析法可以在时域上计算系统发生摩擦自激振动时的动态响应。此时，轮轨系统的运动方程可以写为如下形式[23]

(1)

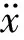
(2)

(3)

其中，β=(1-α2)/4；γ=0.5-α；-1/3≤α≤0。通过将时间t设为t+Δt，即可进行下一个时间增量步的计算。

1.3 摩擦自激振动导致钢轨波磨的理论分析

在铁路研究领域认为轮轨间摩擦功的周期性变化是导致钢轨表面波浪形磨损的主要原因。因此，这里通过车轮与钢轨之间摩擦功的变化来研究轮轨系统摩擦自激振动与钢轨波磨之间的关系。Brockley从摩擦功的角度提出了一个钢轨磨损公式，其简化形式如下

w=K(H-C)

(4)

式中：w为单位时间内的磨损量；K为磨损系数；H为摩擦功(H=Fvr，F为摩擦力，vr为相对滑动速度)；C为耐久性摩擦功。

当车辆通过小半径曲线轨道时，导向轮对上内轮和外轮的蠕滑力均可达到饱和状态。当车轮与钢轨间的蠕滑力达到饱和时，蠕滑力F等于摩擦力，即F=μN，其中μ为车轮与钢轨之间的摩擦因数，N为车轮与钢轨之间的法向接触力。车轮的横向相对滑动速度为vr=Ψ×v，其中Ψ为车轮的冲角，v为车轮的前进速度。在瞬时动态分析过程中，μ，Ψ和v均假设为常数。

在前期的研究中发现，当轮轨系统发生摩擦自激振动时，车轮与钢轨之间的法向接触力也发生了同频率的振动。因此，车轮与钢轨之间的摩擦功也发生了同频率的波动。根据式(4)，可以发现当轮轨系统发生摩擦自激振动时，车轮与钢轨之间单位时间内的磨损量也同样发生了周期性的波动(频率与自激振动相同)，进而引发钢轨波磨。

2 结论与讨论

2.1 轮轨系统动态响应的现场测试

在现场测试中，使用B&K公司4507-C加速度传感器测量钢轨的垂向振动加速度，该传感器的最大测量加速度为20 000 m/s2，测量的频率范围为0.1～6 000 Hz。使用B&K公司4518加速度传感器测量轨枕的垂向振动加速度，该传感器最大测量加速度5 000 m/s2，测量频率范围1～20 000 Hz。振动信号的采样频率为16 000 Hz。图4，5，6分别为列车通过短轨枕整体道床轨道时轨枕上方钢轨测点，跨中处钢轨测点和轨枕上测点的垂向振动加速度。可以看出，无论在该区段的任意测点，曲线里轨振动加速度的振幅均明显大于曲线外轨振动加速度的振幅。由此可以证明在小半径曲线轨道上轮轨间的不稳定振动主要发生在低轨上。通过对钢轨和轨枕测点的振动加速度进行功率谱密度分析(PSD)，可以发现，无论是钢轨还是轨枕的振动，其第一主频均在80 Hz左右。因此，本文仅列出了图4中轨枕上方轨头垂向振动加速度的功率谱，如图7所示。可以发现在里轨上的主频为80 Hz，在外轨上的主频为80 Hz和219 Hz。由于该处为小半径曲线，且距离站台较近，经测量该区段列车的运行速度约为37 km/h，波磨的显著波长为125 mm，则导致波磨产生的主要频率约为82.22 Hz。因此，当车辆通过短轨枕整体道床轨道时，导致波磨产生的主要频率约为80 Hz。这与测试得到振动加速度的主频值一致。这里曲线里轨有波磨但外轨没有明显的波磨，可能是由于里轨波磨引起的振动通过整体轮对传递到外轨，从而引起外轨产生该频率的振动。因此这进一步证明了轮轨间的不稳定振动是导致钢轨波磨产生的主要原因。

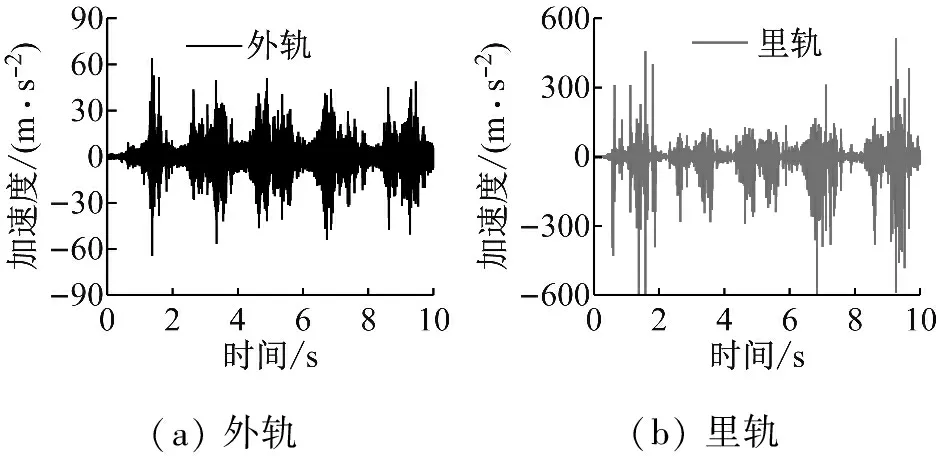
(a) 外轨(b) 里轨

图4 轨枕上方轨头垂向振动加速度测试信号

Fig.4 Measuring signals of vertical vibration acceleration on the rail head above the sleeper

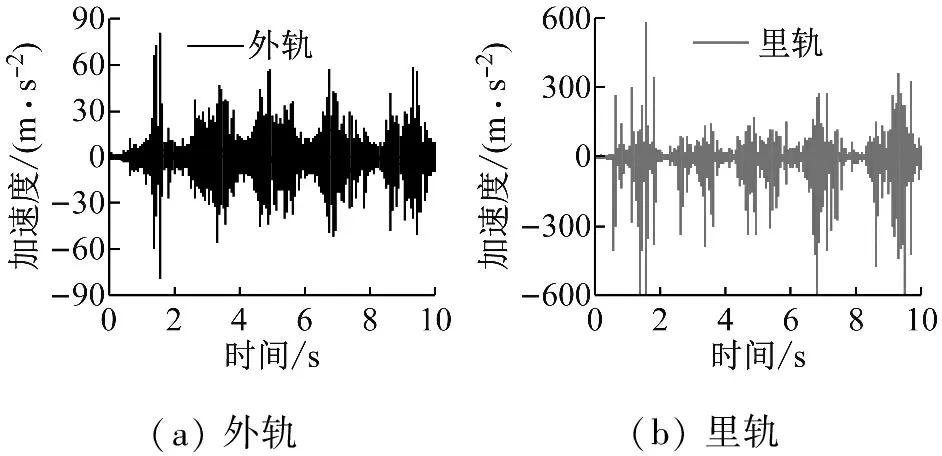
(a) 外轨(b) 里轨

图5 轨枕跨中轨头垂向振动加速度测试信号

Fig.5 Measuring signals of the vertical vibration acceleration on the rail head in the mid-span between two sleepers

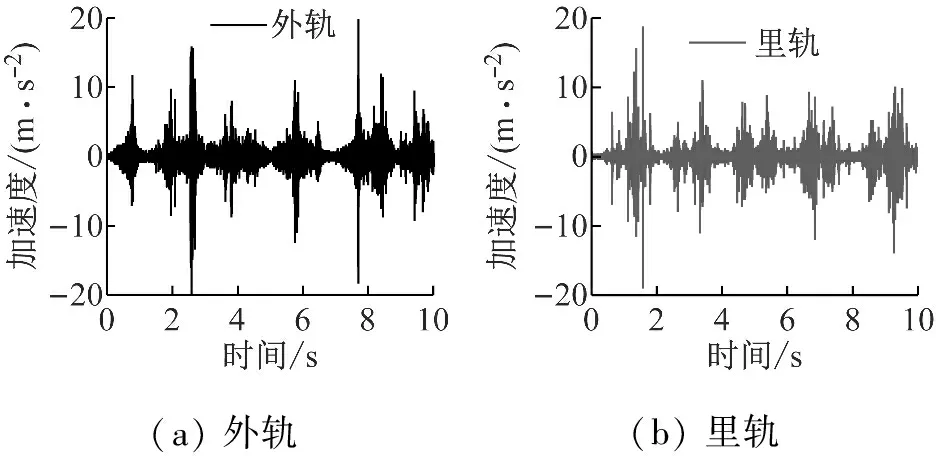
(a) 外轨(b) 里轨

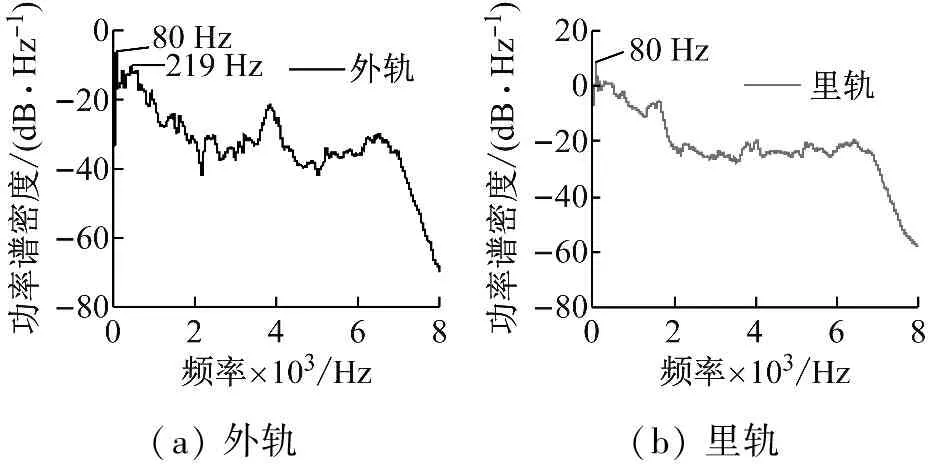
图6 轨枕上垂向振动加速度测试信号

图7 轨枕上方轨头垂向振动加速度功率谱

Fig.7 Power density spectrum analyses of the vertical vibration acceleration

2.2 轮轨系统自激振动的数值模拟

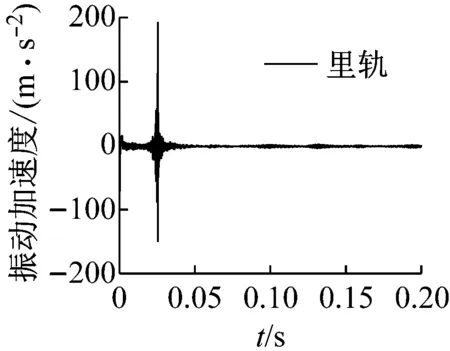
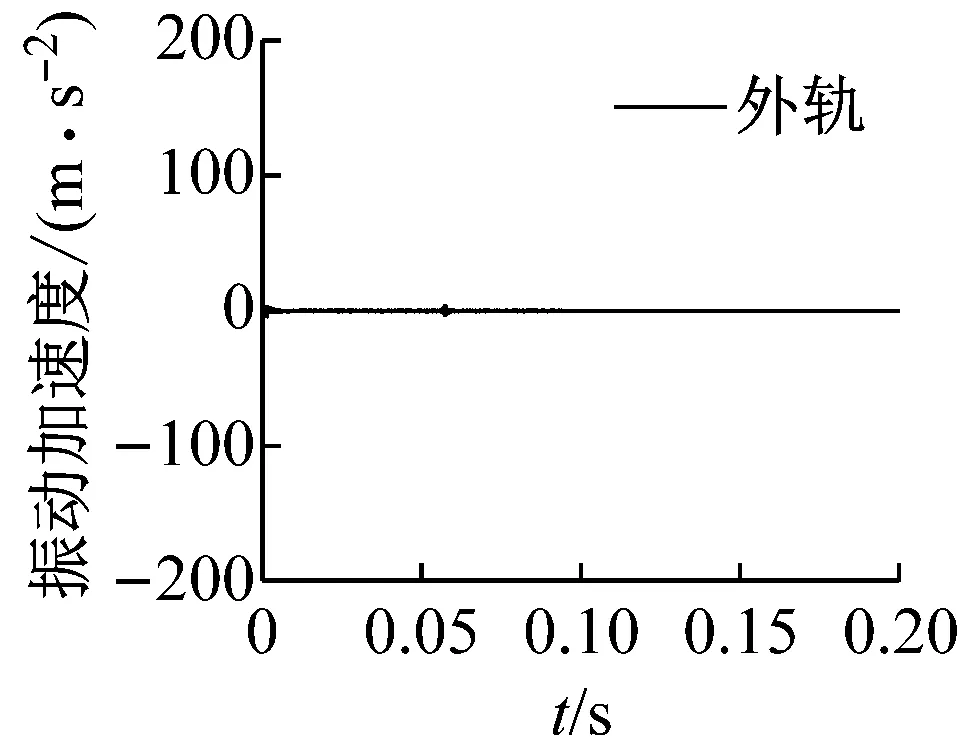
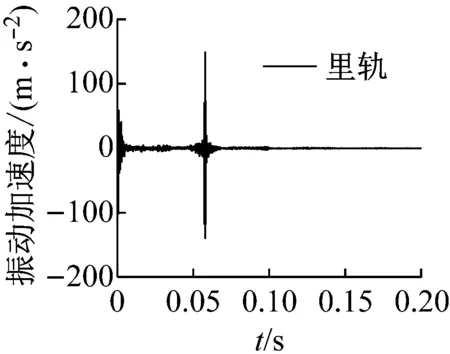
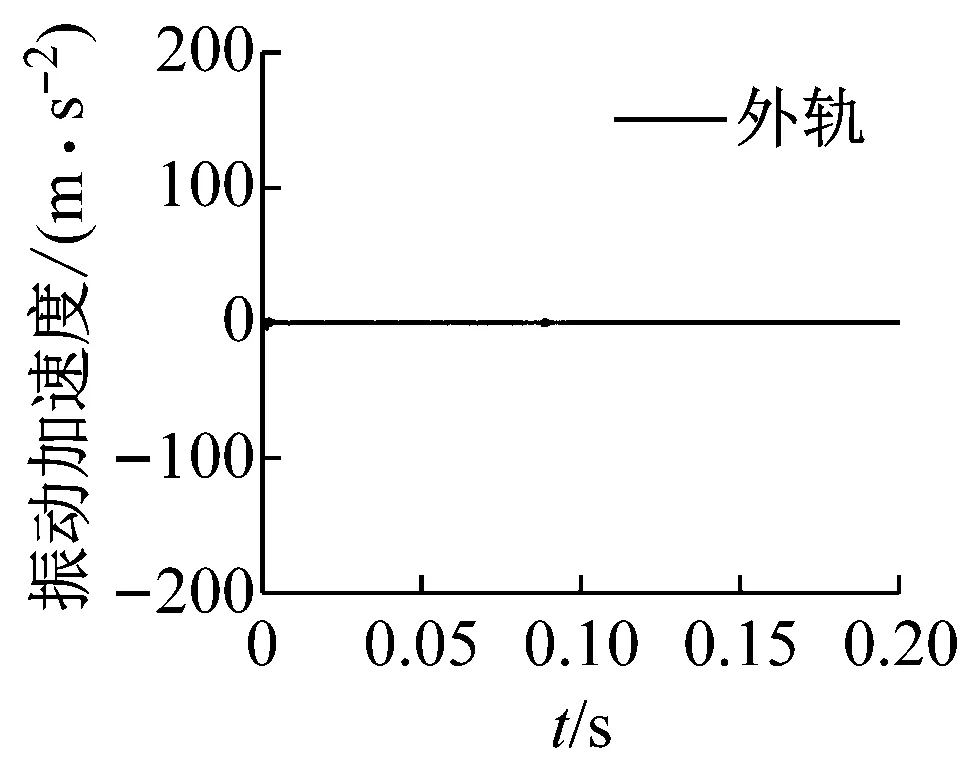
在数值模拟中，可以采用瞬时动态分析进一步研究当轮对通过钢轨测点时的动态特性。测点选取了轮轨接触区域钢轨表面的中心节点，将外轨和里轨上同一位置上的节点设置为一个集合，这里共选取了5组集合，如图8所示。在分析过程中，假设钢轨表面是完全平滑的，轮轨间的摩擦因数为0.4，轮对的初始运动速度设置为37 km/h，在轮对两端添加了大小恒定的悬挂力，无任何外在激励添加，此时在饱和蠕滑力作用下轮轨系统产生的振动为自激振动。为实现轮对处于滚滑状态，使轮轨间的饱和蠕滑力达到饱和，根据式(5)[24]

(5)

式中：T为施加在轮对上的切向力；μ为轮轨间摩擦因数；FSV为轮对的悬挂力。当ξ=0时，轮对处于纯滚动状态，此时接触斑仅存在黏着区。当ξ=1时，轮对处于滚滑状态，此时接触斑仅存在滑移区。而当0<ξ<1时，则为轮轨间正常的滚动状态。为实现轮对的滚滑状态，当ξ=1时，在轮对上施加了T=13.98 kN的切向力。图9显示了在测点位置外轨和里轨表面振动加速度的动态响应。可以发现，随着轮对的运行，当轮对通过相应测试点时，钢轨表面振动加速度的振幅最大，这意味着此时发生了摩擦自激振动。并且，可以发现同一集合里轨表面振动加速度的振幅明显大于外轨。这进一步说明了由轮轨间饱和蠕滑力导致的轮轨摩擦自激振动主要发生在里轨上，该不稳定振动可能会导致钢轨波磨的产生。

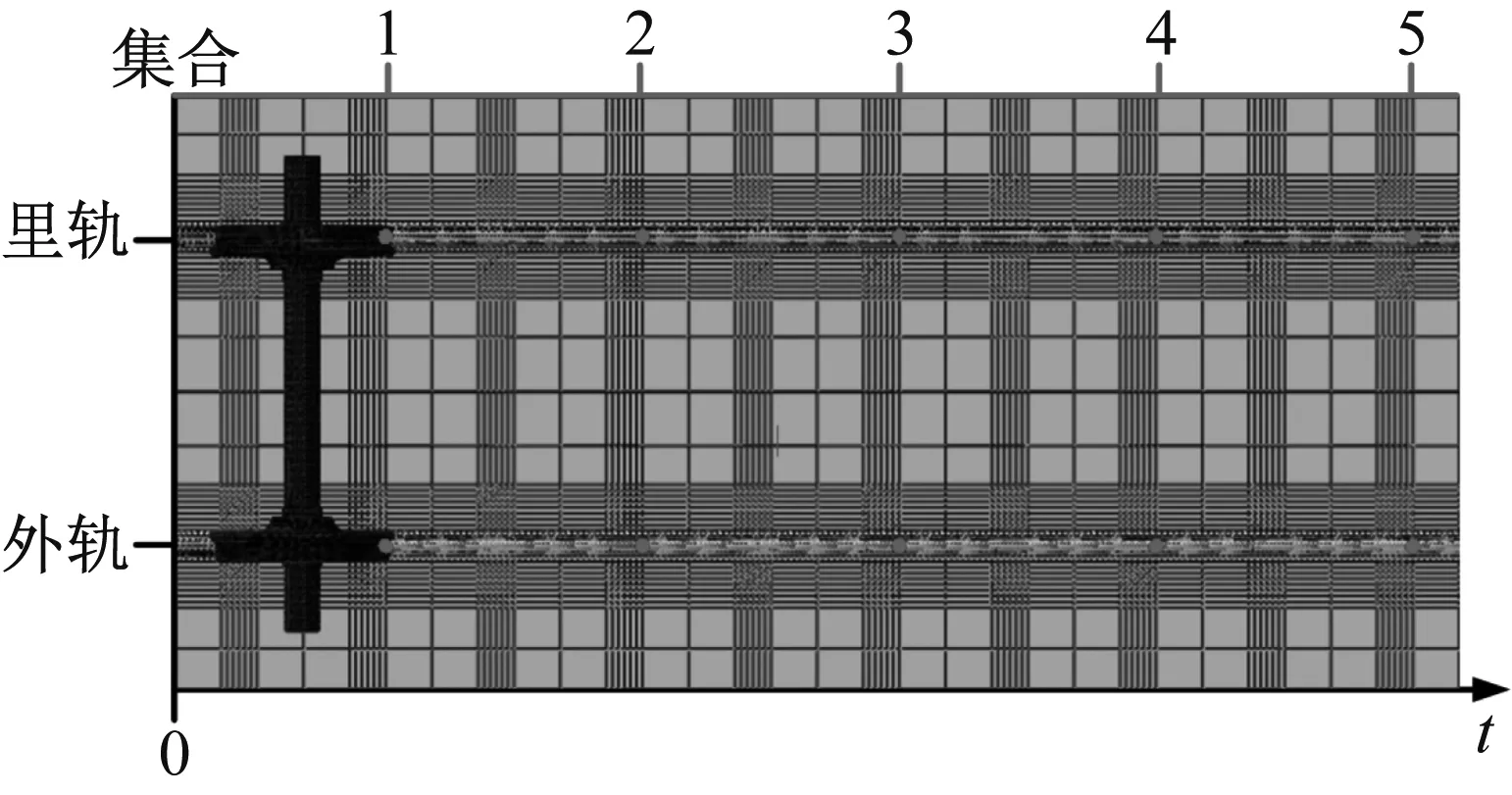
图8 钢轨表面的测试点

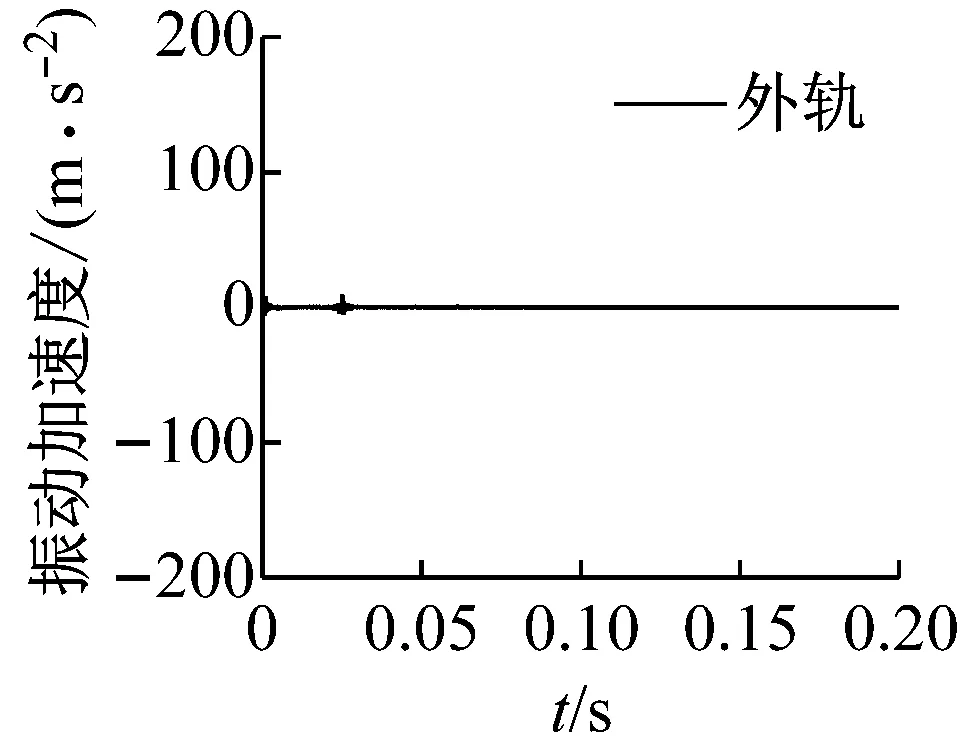
(a) 集合1

(b) 集合2

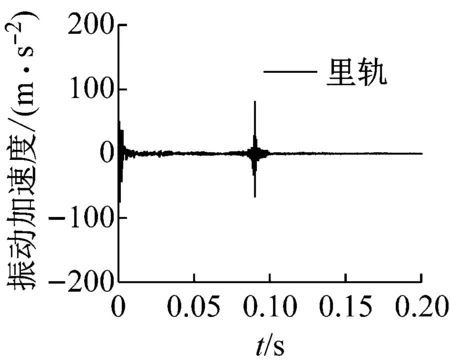
(c) 集合3

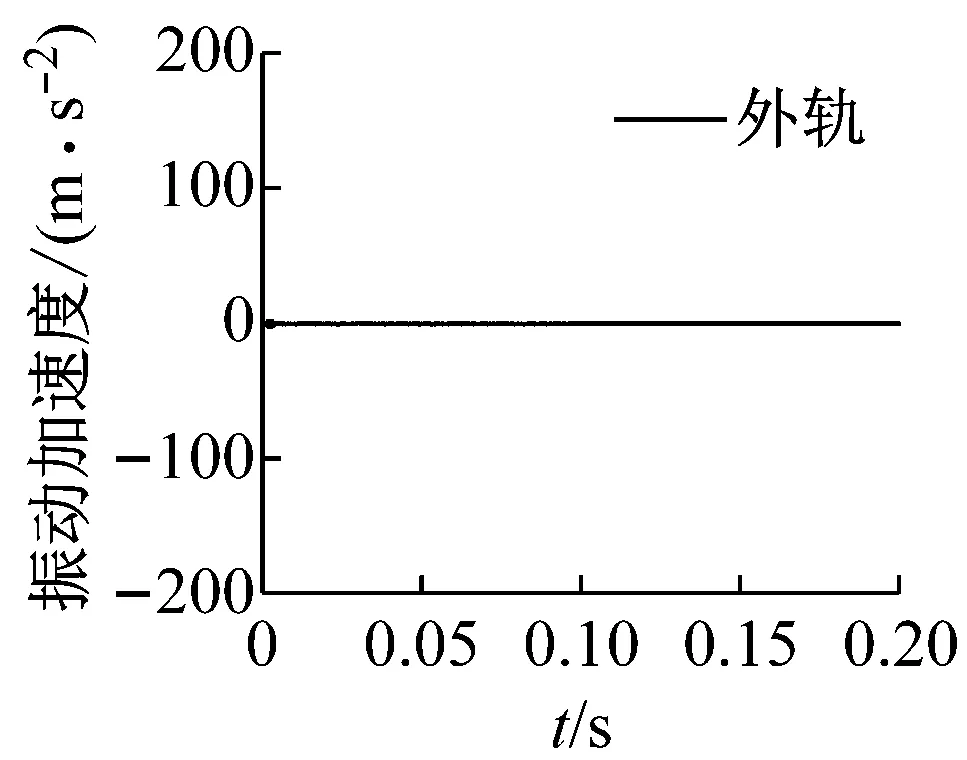
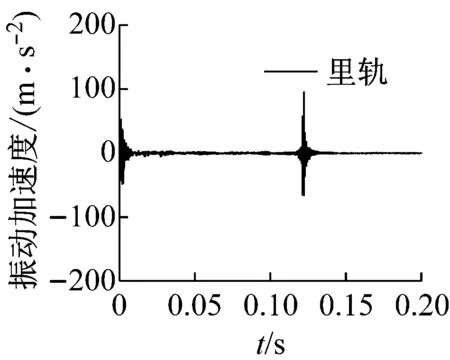
(d) 集合4

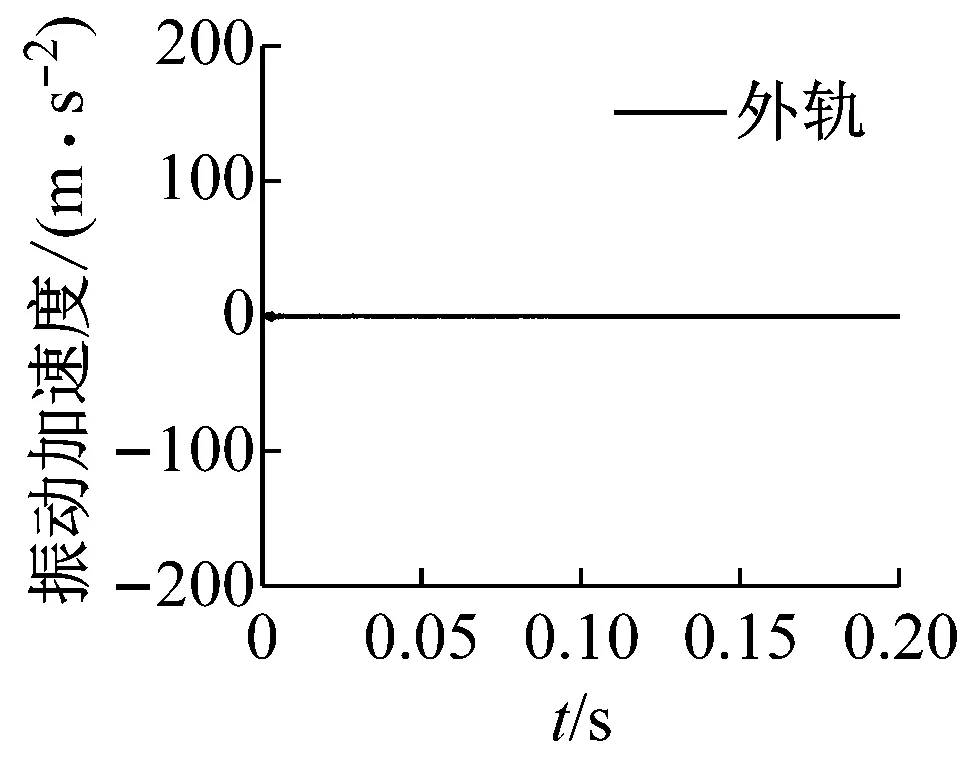
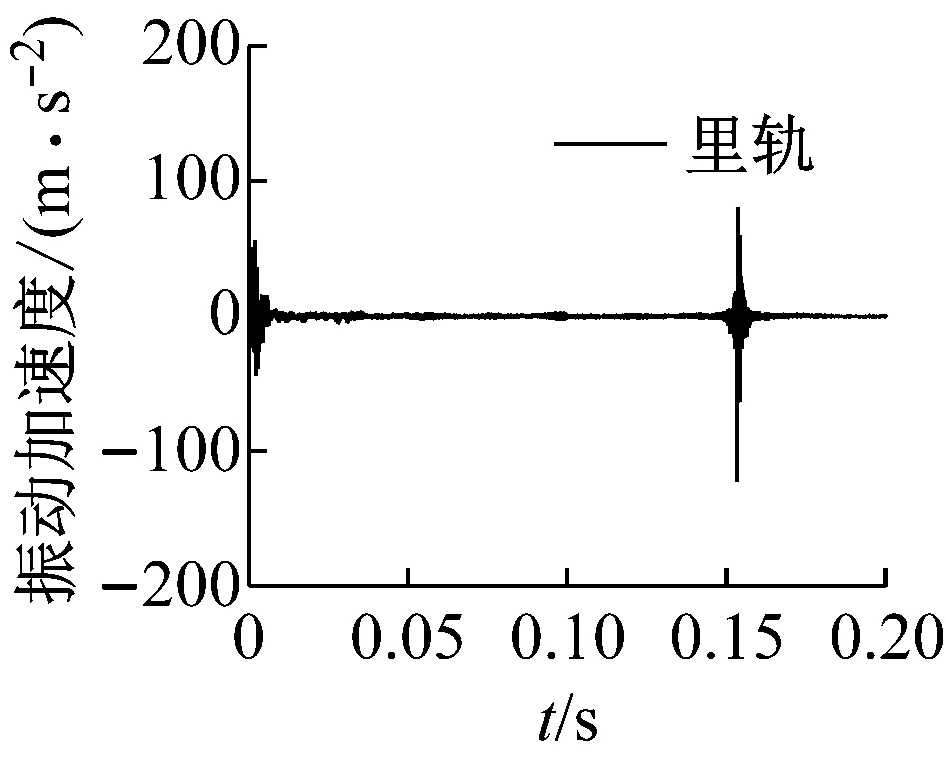
(e) 集合5

为了进一步验证短轨枕整体道床轨道钢轨波磨的形成机理，采用复特征值分析法提取了该轮轨系统的自激振动频率与模态，如图10所示。其中，等效阻尼比是衡量自激振动发生趋势的一个重要参数。当等效阻尼比为负数时，表明此时系统不稳定，可能发生摩擦自激振动。并且该值越小，相应的自激振动越容易发生。此时，系统的最小的负等效阻尼比为-0.015 48，对应的主要不稳定振动频率为86.36 Hz，其不稳定振动主要发生在轮轨系统的内轮和里轨上。此时，预测得到在里轨上波磨的波长约为119 mm，这与现场测试波长近乎一致。因此进一步确认了轮轨间的饱和蠕滑力导致的轮轨摩擦自激振动是导致钢轨波磨产生的主要原因。

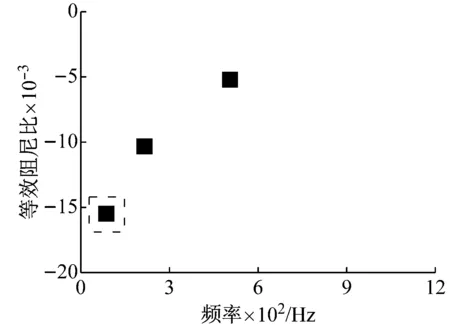
(a) 负等效阻尼比分布

(b) 不稳定振动模态

Fig.10 Distribution of effective damping ratios and mode shape of friction-induced vibration of the wheelset-track system

3 结 论

本文基于摩擦耦合自激振动导致钢轨波磨的观点分别采用现场测试和数值仿真的方法对短轨枕整体道床小半径曲线轨道上的钢轨波磨进行了研究。在现场测试中，分别测量了车辆通过时外轨和里轨轨枕上方和跨中处钢轨上的垂向振动加速度和轨枕上的垂向振动加速度。在数值仿真中，建立了短轨枕整体道床小半径曲线轨道上导向轮对-钢轨模型，并分别采用瞬时动态分析和复特征值分析研究了其不稳定振动的动态特性和振动模态。综合对比现场测试和数值仿真的结果，可以得到以下结论：

(1) 当车辆通过短轨枕整体道床支撑的小半径曲线轨道时，里轨上振动加速度的振幅明显大于外轨上振动加速度的振幅，因此轮轨间的不稳定振动主要发生在里轨上。

(2) 在短轨枕整体道床支撑的小半径曲线轨道上，综合现场测试和数值仿真预测得到的主要不稳定振动频率约为80 Hz，这与现场测试中导致波磨产生的主要频率近乎一致。

(3) 轮轨间的饱和蠕滑力能够导致摩擦自激振动产生，该不稳定振动是导致钢轨波磨产生的主要原因。

致谢：特别感谢西南交通大学金学松教授邀请陈光雄教授参加了北京地铁四号线的现场测试。