一种考虑钢材硬化各向同性的失效准则在船舶碰撞数值仿真中的应用

赵百惠， 胡志强， 陈 刚

(1. 上海交通大学 海洋工程国家重点实验室， 上海 200240； 2. 英国纽卡斯尔大学 海洋科学与技术学院， 纽卡斯尔， 英国 NE1 7RU； 3. 高新船舶与深海开发装备协同创新中心， 上海交通大学， 上海 200240；4. 中国船舶及海洋工程设计研究院， 上海 200011)

尽管全球各国均努力防止船舶事故，船舶泄漏污染仍时有发生。发生泄漏污染的主要原因之一是船舶在碰撞和搁浅事故中船体结构断裂破损。船舶事故不仅会引起漏油和永久性的船舶结构损坏，而且可能导致人员损失和船舶交通堵塞，并对海洋环境造成恶劣影响[1]。除了规范全球船舶运输行为，增强船上人员安全意识之外，在设计阶段预报分析船体结构抗撞能力，并对船体结构进行优化，也是有效减少石油泄漏事故发生的重要措施。

船舶碰撞与搁浅研究方法一般分为三类，即试验法，简化解析法和有限元数值模拟法。其中，试验一般可以提供较为精确和可靠的预测，然而因其需要大量人力和时间，而且价格昂贵，实船试验很少进行。自20世纪90年代后期[2]，计算机技术的迅速发展使得大尺寸复杂结构船体模型的有限元数值仿真变得可行；相对而言，解析方法的发展较为缓慢。为了满足造船工业对可靠性和降低成本的效益日益增长的需求，有限元仿真技术在船舶防撞性的直接定量预报以及搁浅场景的模拟应用更加频繁。此外，数值仿真技术还经常用于对简化解析方法的验证应用[3]。

在船舶碰撞与搁浅的有限元数值仿真过程中，判断模拟钢板材料的有限元单元的断裂失效，是一个十分重要的问题。例如，在球鼻艏撞击船侧结构时，船体外板的膜拉伸，是最主要的结构吸能形式。而一旦外板破裂，其吸收能量的能力会大幅度下降。外板破裂早了，低估了外板的吸能能力；外板破裂迟了，则高估了外板的吸能能力。因此，准确预报板材破裂，合理分析船舶的防撞性，就显得十分关键。但是，不同的学者，当利用有限元方法进行数值仿真时，即使是研究同一个对象，也会得出不同的计算结果。造成这一情况的原因主要包括失效准则不同，有限元模型网格尺寸不同，使用的计算程序不同等原因[4]。其中，板材单元失效准则以及网格尺寸是两个主要原因，并且二者相互影响。

当前国际学术界对船舶碰撞搁浅有限元应用中的钢材断裂失效准则已进行了大量研究。Hill[5]基于局部颈缩分析提出了判断塑性开始的简化方法，为BWH失效准则的基础。Törnqvist[6]依据系列拉伸试验、压痕试验和三点弯曲试验数据，改进并验证了RTCL准则[7]。Stoughton等[8]提出了基于应力状态的成形极限图，避免了金属对于应变路径的依赖问题。在船舶碰撞搁浅的仿真分析中，目前采用较为简化的临界等效塑性应变法，而上述钢材断裂失效准则因其复杂性尚未得到广泛应用。本文主要研究目的是基于国际学术界现有的失效准则，推导出一个改进的钢板板材断裂失效准则。通过验证其合理性，对推广更具准确性的新型失效准则具有重要意义。

1 有限元应用中的钢材断裂失效准则

目前，在船舶碰撞搁浅的有限元研究领域，国际学术界已经提出了多种钢板材料失效准则。它们各有优缺点和不同的模拟适用场景，且均在进一步完善发展中。

1.1 临界等效塑性应变法

对于一种材料，对应一个经验塑性应变临界值εcr，当厚度方向应变达到此临界值，则认为断裂发生。因此，临界等效塑性应变法是在碰撞模拟中最简便常用的方法。但此失效准则基于较为简化，没有考虑应力状态的影响，结果并不十分准确[9]。

1.2 基于应变状态的成形极限图(FLD/FLC)

基于应变状态的成形极限图最开始由Keeler等[10]提出。此方法主要是通过材料在单向或双向应力作用下，给出其在不同的应变路径中得到的局部失稳极限应变ε1和ε2，以此为横纵坐标绘制出条带形的区域或曲线，得到此种材料的成形极限图。在判断材料失效时，将塑性失效初期的主应变(ε1,ε2)在成形极限图中描绘出来，如果落在成形极限图的成形极限曲线上部，板材变形时就会产生破裂，反之则是安全的。基于应变的成形极限图的一般形式，如图1所示。

图1 基于应变状态的成形极限图一般形式

1.3 基于应力状态的成形极限图FLD/FLC

在发现基于应变的成形极限曲线的局限性后，Arrieux等[12]提出对于基于应变的成型极限曲线的改进。之后，Stoughton等[13]通过转换应力应变状态提出了基于应力状态的成形极限图。Stoughton通过对同一金属样本不同预应变情况下进行拉伸试验，发现得到的成型极限曲线差别较大，证实了基于应变状态得到的成形极限图对于应变路径的依赖。随后，将曲线转化成应力状态下成形极限图，可以发现非线性的应变变化路径对基于应力状态的成形极限图影响不大。

Jie等[14]对此方法进行了改进，并将其应用于有限元法，证明了此方法在数值模拟中输入的参数简单，与实验结果的比对也较合理。

1.4 RTCL失效准则

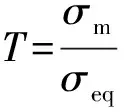
(1)

当失效累积到一个临界值时，认为断裂开始。累积的失效值可以表示为

(2)

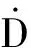
在有限元模拟中，一旦积分点积累的失效值达到临界值Dcr，则单元失效，从有限元结构中移除，表示断裂失效开始。

1.5 BWH失效准则

金属在断裂之前通常是过度的塑性变形，在板和壳结构中，这经常被看作结构在受到外力后在窄带中的过度塑性流动，其特征在于局部颈缩，材料在这个阶段虽然没有断裂，但已达到临界断裂状态。从微观上讲，这是因为在材料中已经出现显著的弱点，其随后将迅速结合并导致金属的断裂。

BWH准则将局部颈缩的开始视为失效，这在对大尺寸板壳结构的碰撞研究中是十分可取的[15]。一方面，结构在发生局部颈缩之后，其应力应变状态均会发生明显改变[16]，在有限元数值模拟中，对于较粗的网格划分无法准确捕捉到此时的状态变化，而较细的网格划分会大大增加计算时间和资源，使用BWH准则可以有效减少网格尺寸的影响。此外，失稳的开始可以基于材料的应力应变曲线给出，简化了此失效准则的检验过程[17]。

2 基于power law材料模型的BWH失效准则理论推导

本文提出一种基于power law材料模型的BWH失效准则，该准则适用于船舶碰撞与搁浅的数值仿真分析。

2.1 材料模型

材料模型的选择是钢材断裂失效准则的基础。考虑各向同性的塑性硬化材料，材料应力-应变曲线由Ludwik’ s power law公式表示，即

σ=Kεn

(3)

式中：K和n为材料的特定常数。

2.2 失效模型

Hill于1952年初步提出以局部颈缩开始判断钢材失效的失效准则。Hill假定颈缩方向与最大主应力成φ角度，一旦颈缩形成，沿颈缩带方向的应变增量为0，则有

(4)

颈缩形成时，应变硬化效果与厚度方向上的尺寸减少并互相平衡，得到

(5)

一般认为主应力增量比例与主应力之间比例一致，即

(6)

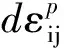
(7)

式中：dλ为一非负的比例系数。

在线弹性阶段，应力应变满足Hook定律，存在比例对应的关系；而在塑性变形阶段，应力与应变之间不再存在比例对应关系，应变不仅和应力状态有关，还和变形历史有关，此时则需要研究应力与应变增量之间的关系，这种增量形式表示的塑形本构关系称为增量理论。由塑性力学增量理论，塑性应变增量可表示为

(8)

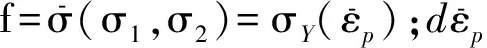
屈服函数f为势函数，考虑屈服函数变化量的两种表示方法

(9)

又由塑性流动理论，可得

(10)

(11)

若用最大主应力表示，则有

(12)

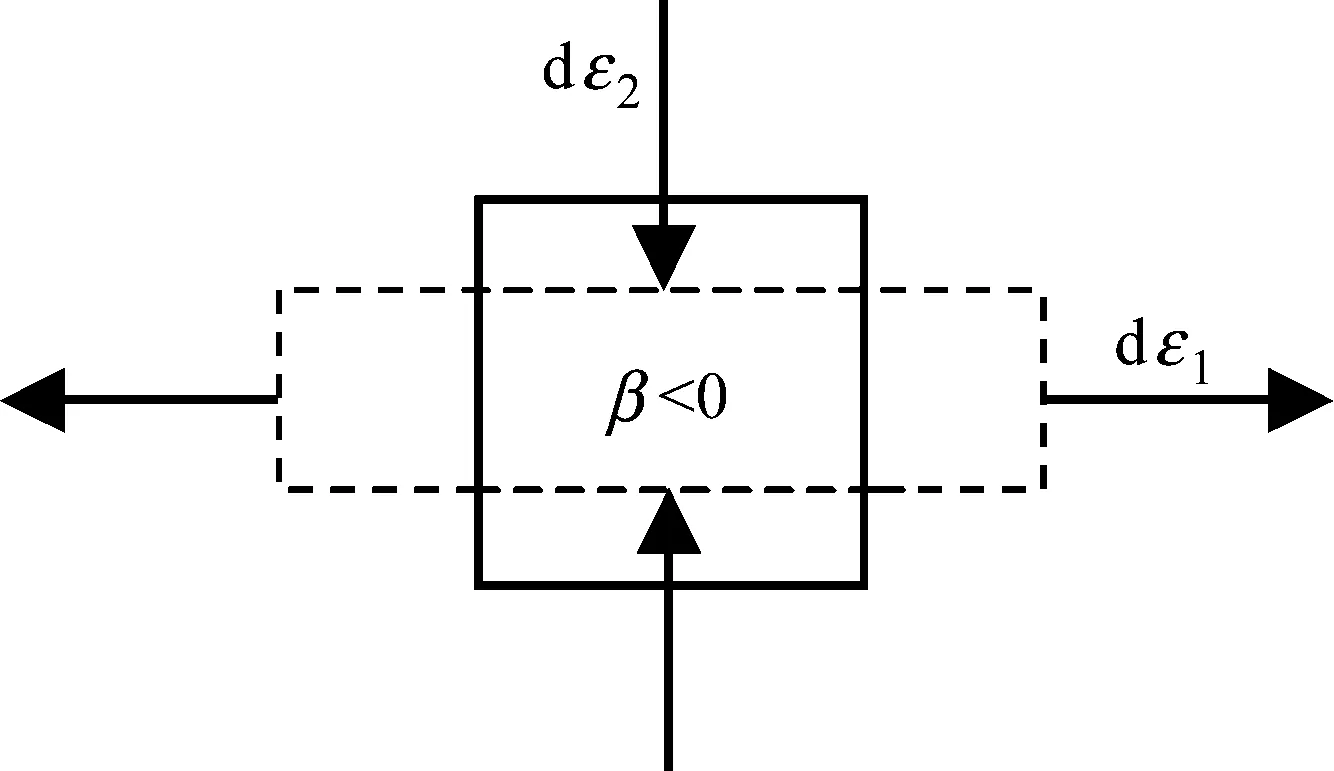
需注意的是，上文提出的失效准则只适用于β为负值的情况。而在船舶碰撞搁浅事故中，船体结构受外力导致的应变状态是多样的，如图2所示。考虑平面应力状态，会发生剪切、双向拉伸等情况。

(a)

(b)

为使此失效准则适用于不同的应变状态，现基于Bressan与Williams提出的三个假设，推导出适用于β不为负值时的失效模型。Bressan等[18]提出了预测金属成型中局部颈缩的失效准则，它基于以下三个假定:① 剪切失稳发生在这样一个截面，即材料单元沿此截面厚度t方向是没有应变变化的，即dεt=0 ；② 失稳的发生是由于局部剪应力达到临界值，即存在τcr，此为材料的一项基本性质；③ 忽略弹性应变。

图3 应变莫尔圆

由假定①，考虑图3中应变莫尔圆，图3中，A点代表发生剪切失稳的材料单元，其厚度方向应变增量为

0，即

(13)

从而得到

(14)

另外由体积不可压缩条件，即dε1+dε2+dε3=0，有：

dε3=-dε1(1+β)

(15)

可以得到

(16)

由假定②，考虑图4平面应力状态莫尔圆，找到对应τ=τcr的点A，可以得到

(17)

由此，可以得到

(18)

图4 平面应力状态莫尔圆

考虑β=0时Hill的公式，即由

(19)

得到

(20)

综上，可以得出适用于power law 材料模型的BWH失效模型，如下

σ1=

(21)

3 材料失效准则的数值应用和验证

LS-DYNA是著名的通用显示非线性动力分析程序，可以模拟各种复杂的接触非线性、材料非线性和几何非线性问题。对于大部分非线性动力学问题，尤其是大变形结构的瞬时高度非线性问题，如船舶碰撞，对结构整体受力引起的整体应变计算过程当中一般均采用显式求解方法。与隐式求解方法相比，显式求解法不会涉及收敛性问题，也不用联立方程组，避免了因联立方程组而出现病态的无确定解的问题。本文利用LS-DYNA程序开展数值应用和验证工作。

LS-DYNA提供自定义材料的二次开发功能，即编写材料子程序并嵌入LS-DYNA主程序中。LS-DYNA用户材料子程序从主程序得到应变值，且返回相关应力值，因此二次开发的关键问题为编写材料的自定义本构关系。下面给出通过非线性有限元方法中应力更新算法中的半隐式向后Euler算法，依据上述失效准则作为判定，编写此材料二次开发材料子程序的主要过程。

3.1 非线性有限元方法——图形返回算法

在有限元计算时，单元的特性用单元刚度矩阵表示，计算刚度矩阵时，需要进行数值积分。在LS-DYNA中采用的数值积分方法为高斯积分法，因此积分点也称高斯积分点，单元的应力值由返回给高斯积分点的应力值表示，而计算此应力值的过程是较为复杂的，常用的算法即为非线性有限元之中的应力更新算法。

积分率本构方程的数值算法称为应力更新算法。应力更新算法可分为向前和向后Euler算法，前者公式简单易于编程，但应力和内变量的更新值并不满足屈服条件，常常导致不精确的结果；而向后Euler算法，它强化在时间步结束时屈服条件的一致性，即保证fn+1=0(f为屈服函数)，以避免离开屈服表面的漂移。有许多不同的积分本构方程算法，本文主要采用广泛应用于实际中的图形返回算法。其一般包括一个初始的弹性预测步，包含(在应力空间)对屈服表面的偏离，以及一个塑性调整步使应力返回到更新后的屈服表面fn+1=0。该方法可以用两个组成部分来概括：一个积分算法，它将一组本构方程转换为一组非线性代数方程；另一部分则是一个对非线性代数方程的求解算法[19]。

积分算法可以写为

εn+1=εn+Δε，

qn+1=qn+Δλn+1hn,

fn+1=f(σn+1,qn+1)=0

(22)

可以注意到塑性应变增量

(23)

则第n+1步的应力可以表示成公式的形式

(24)

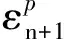
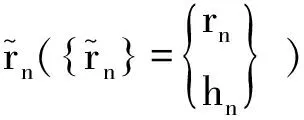
(25)

塑性参数增量为更新其余各变量的基础。本文的材料塑性流动方向与屈服面法线成正比，则认为塑性流动是关联的，即采用关联流动法则，因此r=∂fσ。从而得到塑性参数增量δλ

(26)

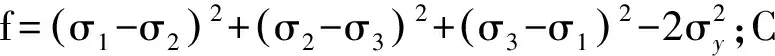
3.2 程序流程图

上述应用于此失效准则的二次开发的图形返回算法可由下文流程图表示。从主程序得到初始值后，首先带入屈服函数检查屈服条件与零关系，若小于零，则退出迭代；若大于零，则计算塑性参数增量，更新各变量值，直至返回屈服面，退出迭代。之后根据此时应力值判断单元是否失效，并返回应力值。

4 数值仿真应用与分析

研究中采用嵌入所提出材料失效准则的LS-DYNA二次开发程序，以一组NSWCCD船模搁浅试验数据为依据[20]，验证所提出的材料失效准则的适用性和合理性。该实验对四种不同双层底结构且缩尺比均为1：5的油船，模拟了在同一礁石下发生搁浅的场景，实验中测出了搁浅过程中的船舶结构受力以及能量耗散情况。本文以其中的一种双层底结构模型为对象，开展有限元建模以及数值计算，将有限元模拟结果与此模型的实验结果进行比较，从而验证断裂失效准则的可靠性。用到的实验基本数据如表1。

实验装置，如图5所示。根据实验要求，礁石顶端从内底板以下约0.05 m处开始进入；同时，船体模型应与水平方向成一定角度，满足当礁石到达后舱壁时，礁石顶端与船模底部距离为两倍双层底间距[21]。

根据实验模型尺寸，由PATRAN所建模型，如图6所示，网格尺寸为30 mm。

表1 船模搁浅实验基本数据

参数数值材料屈服强度σy/MPa283材料极限强度σu/MPa345材料硬化指数n0.22船长/m7.32船宽/m2.54船倾斜角度/(°)3.38礁石顶部半径/m0.17礁石半顶角/(°)45相对速度14 kn(7.202 m/s)

之后将PATRAN中模型以key文件格式输出，在LS-DYNA前处理程序中设置参数，并通过二次开发生成的求解器进行计算。因为本文为自定义的材料模型，在前处理设置参数时需要首先选择相应自定义材料子程序序号；之后，按照子程序中各参数顺序输入对应材料参数，如材料屈服强度、泊松比、硬化参数等。有限元仿真计算时间约为24 h。搁浅场景数值仿真结构损伤截图，如图7所示。

图5 实验装置图(Rodd, 1996)

图6 NSWCCD搁浅实验船模有限元模型

图7 搁浅场景数值仿真结果

图8 结构变形阻力对比结果

图9 结构变形能对比结果

结构变形阻力和结构变形能的数值仿真结果与实验结果对比，如图8、图9所示。从两图中可知，本文推导出的失效模型数值分析得到的结果与传统的临界等效塑性应变方法模拟得到的结果相比，对于结构变形阻力以及结构变形能的模拟结果，均与实验结果更为接近。因此，此种基于BWH失效准则的失效模型具有较高的可靠性，并具有比传统失效应变方法精度更高的优点。

5 结 论

本文依据BWH钢材断裂失效准则的理论推导了基于power law材料模型的失效准则公式，并利用非线性有限元方法中的图形返回算法，结合LS-DYNA材料二次开发理论，将此失效准则编程后嵌入了LS-DYNA程序中。利用更新后的LS-DYNA程序，以NSWCCD进行的一项实验模型为对象，进行了有限元数值模拟，并与实验结果和经验等效塑性应变模拟结果对比，证实了此失效准则的可靠性以及更高的准确性。

此失效准则以局部颈缩开始作为判断失效依据，避免了后颈缩区域的分析，因此对网格尺寸不敏感。也因此，此失效准则的使用尚有局限性和不确定性。此外，在前处理中输入参数较多，流程较复杂，使用起来不如传统的临界塑性失效应变方法简便。钢材断裂的失效准则仍需后续发展和改进，从而达到更广泛的应用。