电子节气门有限时间收敛反步控制器设计＊

郑朋涛 孙建民

（北京建筑大学 城市轨道交通车辆服役性能保障北京市重点试验室，北京 102616）

主题词：电子节气门 Lyapunov稳定性理论 反步滑模控制 有限时间收敛

1 前言

电子节气门控制系统是发动机电子控制系统中的重要组成部分，对提高汽车的动力性、燃油经济性和发动机排放性能有很大影响，因而改进电子节气门空燃比控制具有重要意义，开发响应速度快、鲁棒性强、稳态性能好等的控制器成为一种需求。

目前，研究人员开发出了许多电子节气门控制器，如PID控制器、模糊自适应控制器、自适应控制器、反演控制器、滑模控制器和预测控制器[1-6]等。本文在前人研究的基础上，提出并设计一种电子节气门有限时间无抖振反步滑模控制器，进一步提高了发动机电子节气门对空燃比的控制精度，改善了发动机的排放性能。

2 带扰动的非线性电子节气门数学模型建立

电子节气门主要由电子控制单元、直流电动机、减速齿轮、节气门体、回位弹簧和阀片等组成[7]，电子节气门具有很强的非线性特性、模型不确定性、易受外界干扰等特点，难以保证电子节气门开度在发动机各工况下的精确控制。为此，建模时将模型参数不确定性、外界扰动及角速度项等考虑为扰动项，则电子节气门数学模型表达式为：

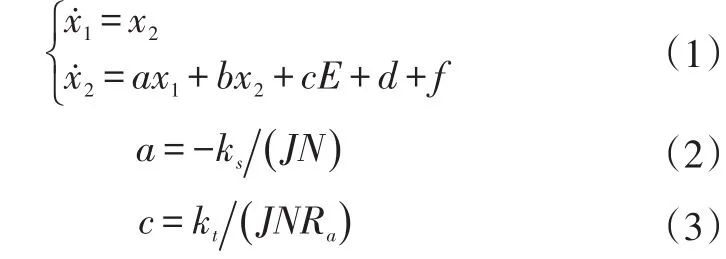
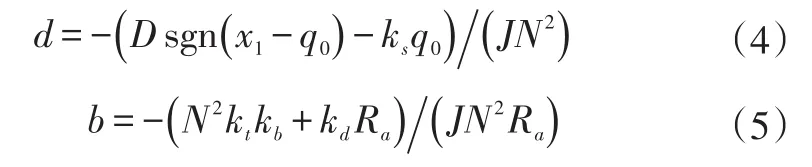
式中，f为扰动项；x1为节气门阀片转角；x2为阀片转速；q0为节气门“跛行”平衡位置角度；E为电机电压；Ra为电机绕组电阻；kb为电机反向电动势系数；N为减速齿轮组减速比；J为电机主轴转动惯量；ks为回位弹簧系数；D为回位弹簧扭矩系数补偿；kd为节气门轴粘性摩擦系数；kt为电机扭矩系数。

3 有限时间收敛无抖振反步滑模控制器的设计

为设计一款具有较强鲁棒性，即具有较好的跟随特性和抵抗外部干扰能力的电子节气门控制器，以满足发动机在各种运行工况下的性能需要，采取了如图1所示的控制策略。该控制策略中，有限时间收敛滑模控制器是采用有限时间收敛终端滑模面设计的，因该控制器中存在未知状态量x2和扰动量f，所以分别设计降阶状态观测器和非线性干扰观测器对这两个量进行观测。

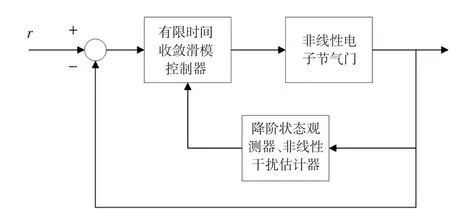
图1 控制策略

3.1 有限时间收敛终端滑模面

基于有限时间收敛原理[8]，在任何控制系统中，若该控制系统的状态变量x满足关系ẋ=-k1x-k2sgn()x，则状态变量x将会在有限时间内趋近于零点。该有限时间为且要求x0、k1、k2都大于零。有限时间T与k1、k2两个参数有关，通过配置两个参数的值来调节系统在有限时间内收敛。

采用上述状态方程设计新形式的终端滑模面[9]以加快系统的收敛速度，且保证系统能在有限时间内收敛。令系统误差e=e(t)，则终端滑模面为：

如果状态变量能在滑模面上产生滑模运动，则需要满足下式：

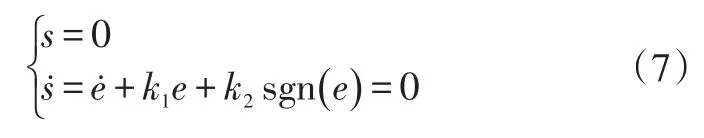
基于Lyapunov稳定性定理分析，取Lyapunov函数为，将式（7）变形代入得表明该终端滑模面可使系统渐进稳定。由上述有限时间收敛定理可得：

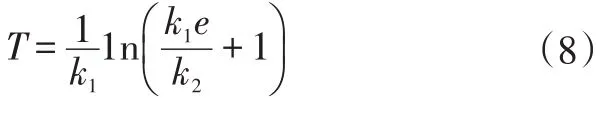
3.2 有限时间收敛反步滑模控制器

通过反步法[10]设计滑模控制器，可使电子节气门系统每个状态变量具有强稳定性。设电子节气门系统的状态变量误差为：

式中，xd为期望信号；m为虚拟控制量。

根据Lyapunov稳定性理论，设Lyapunov函数为：

对式（10）求导得：

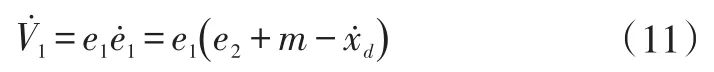
取虚拟控制量m=-p1e1+ẋd（p1＞0），并将其代入式（11）得：

根据Lyapunov稳定性理论可得，随时间的推移系统状态误差e2逐渐趋近于0，则V̇1≤0，表明该子系统渐进稳定。

令q=ax1+bx2+d+f，由式（1）和式（9）得：

设Lyapunov函数为：

对式（14）求导后，再根据式（6）和式（12）得：

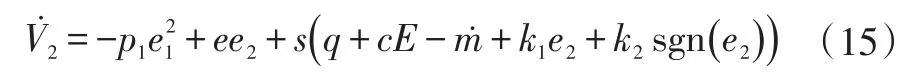
根据Lyapunov稳定性理论，使V̇2≤0保证系统稳定设计控制律，取p2＞0，则控制律为：

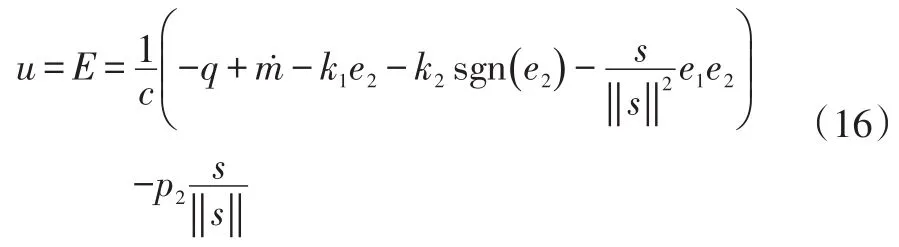
3.3 消抖振控制器和非线性干扰观测器

由于滑模变结构控制存在抖振问题，其主要原因是电子节气门系统在控制过程中的不连续，并且这种抖振还来源于滑模函数在滑模面内外来回切换。前面提出的有限时间反步滑模控制器中，s/‖s‖2和sgn(e2)都会使系统的控制过程出现不连续，从而导致控制中有抖振现象的产生。为避免抖振现象，在有限时间反步滑模控制器中利用式s/(‖s‖2+ε)替换s/‖s‖2，同时用e2/(|e2|+ε)替换sgn(e2)，其中ε一般取一个未知的正数。将（12）式控制律连续化，并将q=ax1+bx2+d+f代入后，消抖振控制器的控制律可表示为：

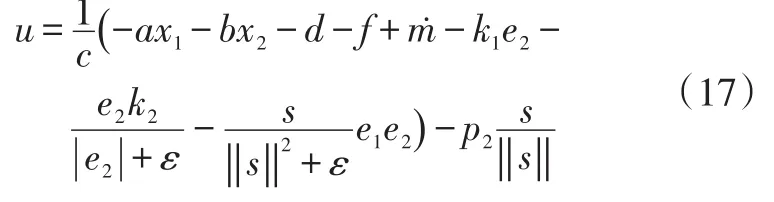
控制系统和控制器中都存在扰动，虽然忽略扰动项、增大滑模系数能克服扰动干扰，但也会使系统产生抖振现象。为解决该问题，通过设计非线性干扰观测器来估计所设计控制器中未知量干扰值f，并对其进行补偿。

非线性干扰观测器主要依据实际输出与估计值的差值补偿来设计，故设计干扰观测器[11]为：

式中，L1为常数。

由式（1）、式（17）和式（18）可得：

设变量

令变量p为

由式（1）、式（18）～式（21）得非线性干扰观测器为：

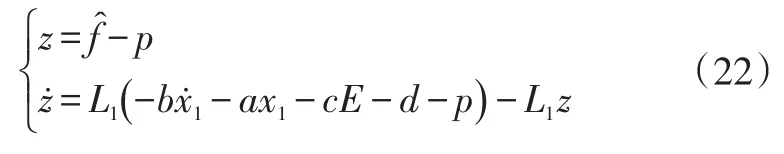
3.4 降阶状态观测器

由于电子节气门阀片转角速度不便于测量，而且基于产品生产经济性考虑，电子节气门在设计时没有安装阀片角速度传感器，即在无抖振控制器中存在未知量x2。为此利用降阶状态观测器[12]来估计不可测量量x2。

设变量：

式中，L2为常数。

将式（1）和式（23）带入式（23）的求导式得：

为了保持未知量之间的无关性，以免增大误差和导致算法代数自回环，故降阶状态观测器中忽略扰动项，即观测器为：

设计降阶状态观测器的误差为：

对式（26）求导，并将式（24）、式（25）代入得：

对式（27）求解得：

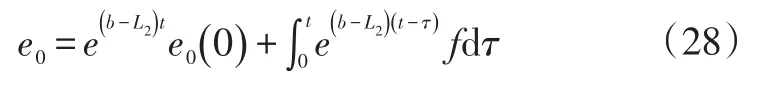
由式（28）可得，b-L2＜0时可保证观测器误差按照指数律下降，故此降阶状态观测器误差值可迅速减小，并趋近于0，保证了观测器的值尽可能准确。

由上述分析可得，降阶状态观测器中各状态值估计表达式为：

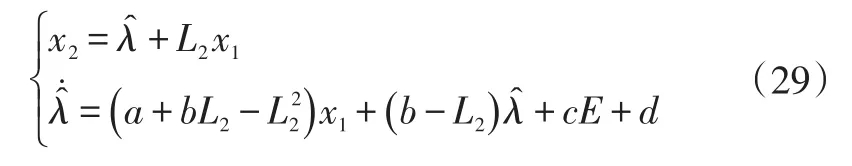
4 试验结果与分析

利用电子节气门建立的数学模型，通过MATLAB/Simulink软件进行仿真试验，以验证所设计的有限时间消抖振反步滑模控制器对电子节气门的适用性。仿真试验主要分析小阶跃信号的响应特性、大阶跃信号的响应特性、稳态响应误差、鲁棒性及方波信号的跟踪特性。

电子节气门性能的参数化评价指标为：

a.从给定控制信号开始，响应曲线首次上升到目标曲线所用时间应小于100 ms，再调节至稳定状态所用时间应小于40 ms，即从给定控制信号开始到稳定状态所用时间不得大于140 ms。

b.给定信号后的响应曲线无超调，以避免节气门阀板碰撞限位；

c.响应曲线的稳态误差保持在±2%之内。

4.1 电子节气门系统阶跃信号响应性能分析

控制信号为小阶跃和大阶跃的响应特性曲线如图2所示，图3为阶跃信号的响应误差曲线，其局部稳态误差如图4所示。

图2 阶跃信号的响应特性曲线

图3 阶跃信号的响应误差曲线

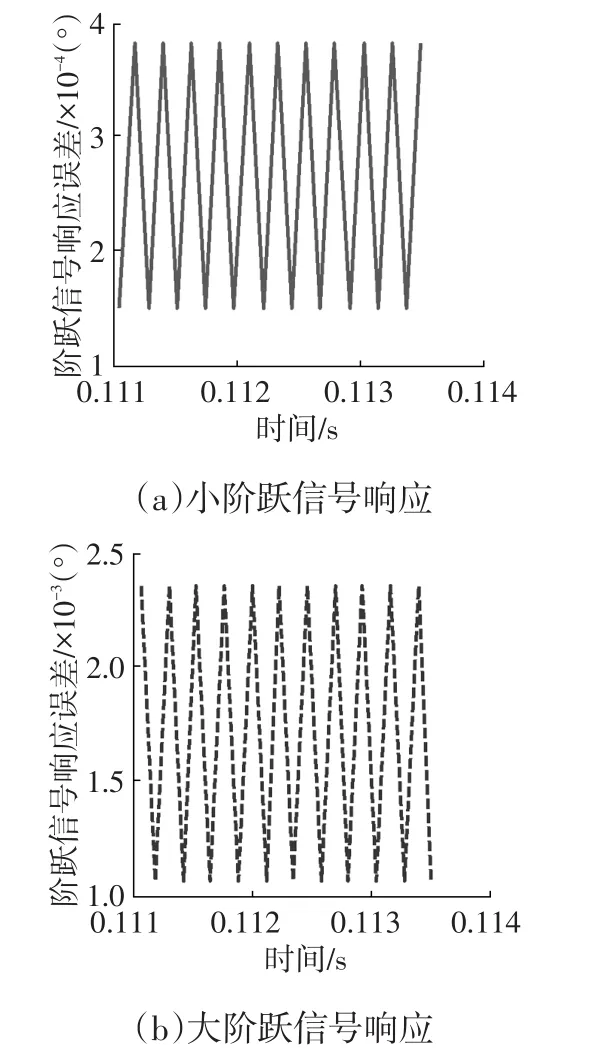
图4 小阶跃和大阶跃信号响应的局部稳态误差

根据仿真试验数据得阶跃信号响应的稳态性能参数如表1所列。由表1、图2～图4可知，当给定控制信号为小阶跃和大阶跃信号时，响应曲线都没有超调量；在给定小阶跃和大阶跃信号时，电子节气门系统的响应调节时间都小于100 ms，在节气门性能要求参数化评价指标范围内，而且基本上为参数化性能指标的1/2；在响应曲线达到稳态时，最大误差量都比要求的标准误差量（±2%）小一个数量级；小阶跃和大阶跃控制信号的调节时间只相差11 ms，且稳态误差范围和最大误差量都满足电子节气门参数化评价指标。

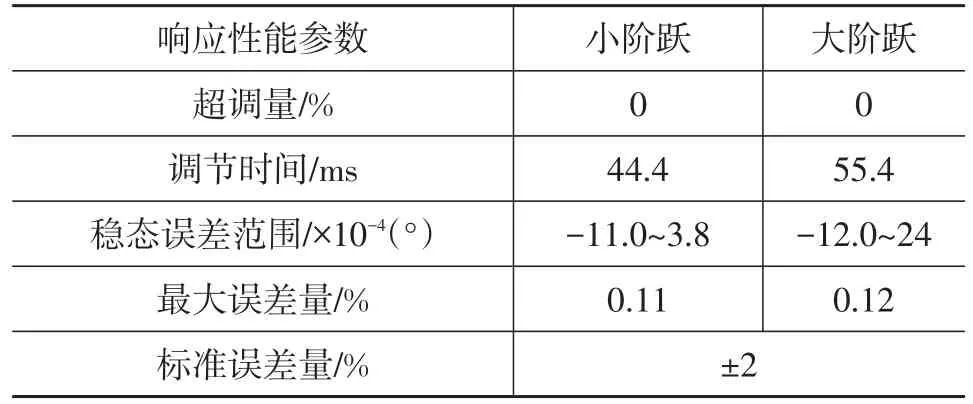
表1 阶跃信号的稳态性能参数

通过上述分析可知，有限时间消抖振反步滑模控制器能满足节气门性能要求的量化指标，说明该控制器响应特性较好。由于图2阶跃响应特性曲线及图3误差曲线光滑，结合图4的局部稳态误差分析，表明阶跃响应曲线稳态精度高、无抖振现象、稳定性好、响应迅速。小阶跃和大阶跃的性能指标相差较小，表明控制器鲁棒特性较好。

4.2 电子节气门系统方波信号响应性能分析

当给定控制信号为方波信号时，电子节气门系统响应特性曲线如图5所示，图6为其误差曲线，其局部特性曲线如图7。方波信号响应的性能指标如表2所列，其中Ti代表给定控制信号第i次突变时响应曲线调节稳定所需要时间，数字1～6表示方波信号突变次数。

图5 方波信号的响应特性曲线

图6 方波信号响应的误差曲线

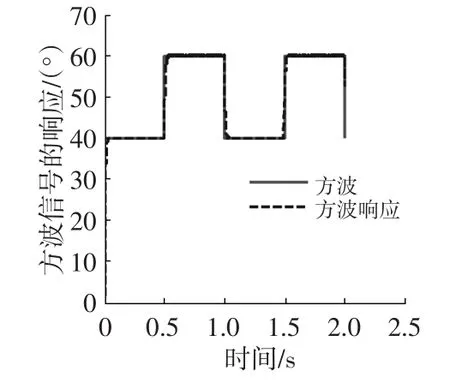
图7 方波信号响应的局部特性曲线

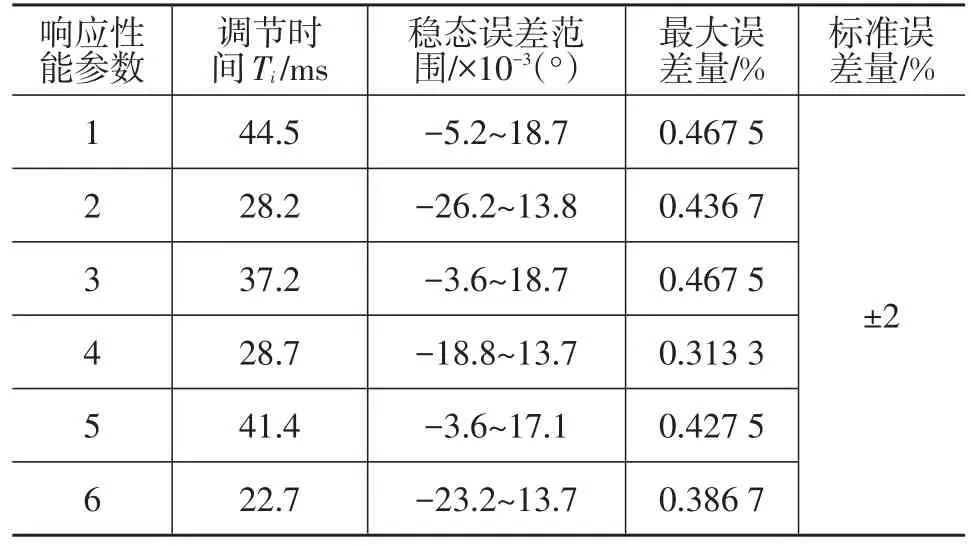
表2 方波响应的性能参数

由表2可知，在目标信号突变时，Ti最大值为44.5 ms，并且Ti值比参数化性能评价指标中稳态调节时间140 ms小很多，可以满足节气门的性能要求；稳态误差范围的最大误差也都比标准误差小一个数量级。由图5～图7可知，这种控制器对方波的跟踪性好，响应迅速，响应的误差曲线最大误差为2（控制信号发生突变时的方波信号高度），并且方波信号的响应特性曲线光滑，最大误差量比参数化标准误差量小一个数量级，表明方波信号的响应抖振很小、稳态精度高、稳态性能好。

5 结束语

为提高发动机电子节气门对空燃比的控制精度，改善发动机的排放性能，针对电子节气门的非线性和易受外部扰动影响，导致电子节气门在控制时收敛速度慢和收敛后控制响应存在抖振的问题，提出一种有限时间收敛无抖振的反步滑模控制方法。经仿真分析表明，电子节气门在给定阶跃信号条件下，其响应在55 ms左右电子节气门控制系统达到稳定，并且稳态精度在1×10-3数量级，表明所设计的控制器具有响应迅速、跟踪性好、稳态性能好、稳态精度高、稳态无抖振、鲁棒性强等特点，对电子节气门的控制有较强的适用性。