在“建构”和“解构”的循环中学习——对“运算律”单元教学的思考

蒋丽英

理论根基不稳定，就无法灵活应用，只是学习空头理论，不会应用，对理论的把握就会出现偏差。总之，要想调和理论与实践的矛盾，就要帮助学生建构运算律，让学生在具体情景中，凭借过往经验，以同化或顺应的方式吸收消化新知。“运算律”的建构，主要包含了建构数学模型和构建数学思想两个方面。

一、建立在“运算律”原始经验上的分析

笔者认为，在正式接触交换律之前，学生对加、乘法交换律并非一无所知，以苏教版教材为例：课本设置了小学生给花浇水的图景，学生解答“共有多少人浇水”时，由于还未形成数字加法计算，也没有学过加法算理，于是，多数学生仍采用原始的“数数”合计的方法。如先数清正在给花卉浇水的有3个学生，又来2个学生帮工，也就是顺着3往后继续数两个序数，于是，一共数到数码5为止，也就是5个学生。当然，也有少数学生逆向思维，以后来加入的2位学生为基准，往后点算3个数序，一直数到数码5为止，于是5为总数。然后，教师牵引学生思考：“通过什么办法，将刚才清点总数的过程用一个简洁的算式表示？”然后及时推出3+2=5或2+3=5两个加式。不难发觉，从一年级“认识加法”开头，学生业已无意识地感触了交换律。以3个浇花的学生为基准，新加入的2个同学汇入其中，或者换个角度，以新加入的2个同学为视角，先到的三位同学算进去，结果都是一样，谁是主体，谁是支脉，交换主次地位，就是加法交换律的“雏形”。

随着时间的推移，心智的成熟，这种“雏形”将日渐完善，这个“规律”将逐渐进驻潜意识成为默认值：两数合并，先后顺序不影响结果。同样，学生对乘法交换律的“雏形”，在二年级已经有了经验胚胎。如二上第一单元“乘法认识”。教材创设这样的情境：依托情境图让学生清点出各种小动物的只数，然后让学生观察所有列出算式的特征，加数相同的加法运算。这种特殊的加法算式有一种简写方式，这种针对特殊加法定制的简式就是乘法。如2+2+2可以写成2×3或3×2。

二、算术意义背景下的运算律教学路径

加乘结合律，是一种另类的交换律，是对交换律的变通和延伸，从两个数出发，引申至更多数，合情推断出三个或以上的数相加，任意交换其中两个加数的位置，和值不变。之所以可以顺利伸延，是因为依仗了对原有乘加法意义的理解。如计算连加2+3+4，表示三个数量的合并，合并就无所谓先后顺序。同理，计算3×2×4时，学生能理解先计算3×2，或者先计算2×4得数一致，三个因数可以随意调换位置。这就是结合律的启蒙运动。教学结合律时，要让学生彻底搞清楚：运算三个数，分次序，与运算两个数不同，除了交换位置还要改变计算工序。为了体现工序改变，一般加“( )”表示。

对于分配律，在二年级计算一位数乘法时也植入了分配律的思想方法。如计算12×4，学生都能将其拆解成12+12+12+12的连加形式，转码成加法时，需将12继续分解成(10+2)，于是得到算式：10+2+10+2+10+2+10+2，根据加法结合律，得到2+2+2+2+10+10+10+10，于是，得到4个2的积与4个10的积相加。因此，用4乘12时，顺其自然想到将12拆解成10+2，然后分别与4相乘，也就是(10+2)×4=10×4+2×4。顺着看，是将12个4分拆成10个4和2个4；倒着看，是10个4再加2个4，一共是12个4。

(一)加法的交换律和结合律

第一层次：可出示教材情境图

在学生得出28+17=17+28之后，教师可激活学生封冻的经验，诱导学生回忆加法意义，让学生利用生活经验揭示交换律的原理。

第二层次：在学生得出28+17+23=？之后，引领学生反思：两个加数可以交换位置，三个加数可行吗？为什么？进而得出三数相加，除了考虑位置变化，还应顾及运算顺序的变化。

(二)乘法的交换律和结合律

第一层次：解封乘法意义。如3+3和2+2+2分别写成什么样的乘法简式？既然乘法是对加法的简化程序，能否由加法的两个运算律推定乘法运算律？用生活经验诠释为什么3+3=2+2+2，也就是3×2=2×3。如让学生数点阵点数。

……

……

横向看，每行3个，一共2行，3×2=6个；纵向看，每列2个，一共3列，所以2×3=6个。于是无论怎么数，都是6个，于是3×2=2×3。

第二层次：引领学生思考，两数相乘适用交换因数位置，三数相乘行得通吗？

(三)乘法的分配律

第一层次：出示计算12×4的竖式。引领学生回顾每个步骤的算理，仍可以用“数形结合”法。如下图中的面积可以怎样算？

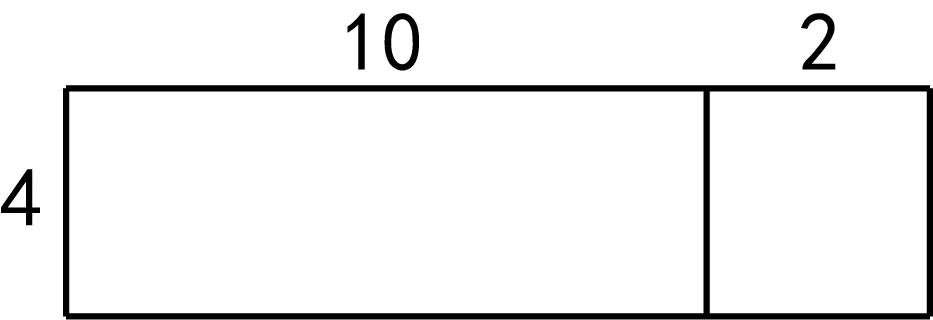
第二层次：指引学生深思，由乘法竖式格式和算理可以推断出什么样的运算律？并用代数式表示。

三、运算律单元教学整体思路的调整

以上教学思路，由原来情境观察提炼法，依托列式，建立在发掘、枚举、论证和归结中得出运算律，形成整体感性认知，发展到唤醒学生封存的经验，解构竖式每一步骤的算理，进行理性分析。最终抽象概括成代数式，并理论服务于实际，在解决问题中学以致用。新思路是：感触、摸索规律→追寻根源→学以致用。“运算律”的存在，是蕴含在计算程序和客观规律上的，是“隐性的客观存在”，而不是随着主观意志改变而改变的。如果先呈现几种不同的算式，生硬地灌输某种规律，然后再进行走过场般的求证，就会有做戏之嫌。

总之，运算律的学习掌握过程就是一步步构建的过程，并在不断的应用中解构。在“建构”与“解构”的反复循环中，学生学到的知识才是具有活性的。