谈谈对数学思维断层现象的分析及思考

刘雅兰

数学教育是数学活动的教育，也是思维活动的教育，保持思维活动的连续性、层进性对于学生清晰地理解问题，把握知识的核心和本质，并且为后续学习扫清障碍，提供支撑都是非常有价值的。本文从三个课例谈对思维断层性分析及策略的思考。

课例一：“乘法的初步认识”。

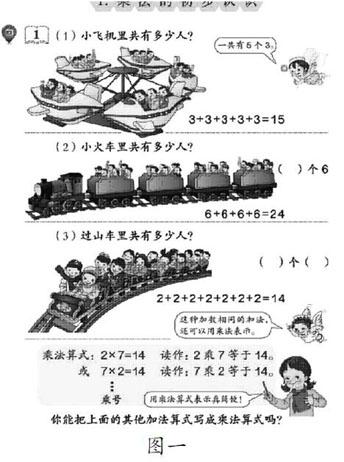
环节一：出示小飞机图（图一），小飞机里共有多少人？

生（1）：15人。

生（2）：3+3+3+3+3=15。

生（3）：还可以用三五十五。

师：这是什么意思？

生：用乘法来计算。

师：乘法？什么情况下用乘法？怎样用乘法呢？

环節二：展开图二（右图），图三（下页左图）的教学，用这样的思维形式引领学生的思考。

生：3+3+3+3+3，一共有5个3，就用5×3来表示。（教师给予及时鼓励。）

课例二：“5的乘法口诀”。

师：现在已经秋季了，小松鼠开始准备过冬的食物了，看看这一地的松果，你能帮小松鼠数数有多少松果吗？

生说可以5个5个数，边叙述边圈画数松果的过程。

师：为了看得清楚，一目了然，老师把这些松果在圈的基础上摆一摆（摆出主题图），这样清楚了吗？

课例三：“乘加、乘减的教学”。

教师让学生观察并解决实际问题，要知道图中圆圈的个数，我们怎么办？

方法一：10+9。

方法二：4×4+3。

方法三：9×2+1。

方法四：10×2-1。

学生找到好多方法来表达自己的思考，课堂比较活跃。然后老师出示一个新的与例题相似模式的图片，让学生在独立解决问题的过程中夯实新知。

课例分析：

一、 关于乘法意义的认识的思维断层型分析

我们在课例一中看到，教材中和教师课堂教学中所倡导的均是这样的一个思维层次，相同加数的加法——几个几——乘法算式。这样的教学中的思维是否是连贯的，是否是清晰的？笔者认为不然。

我们思考原来对于此部分教学，非常强调每份数与份数，而且一定把每份数写在乘法算式中前面的位置，等到学习乘法交换律的时候，再强调两个乘数的位置可以互换。后来教材发生了变化，根据一个加法算式可以写出两个乘法算式，不强调乘数的位置。现在教材这样处理，我们认为它是把这样两个教学进行合理性整合，没有先过分地强调位置，然后再强调位置可互换。这样的处理方式，简化了教学过程，减轻了学生的学习负担。但这样教学是否会缺失一些思考呢？笔者认为我们的乘法学习不仅要让学生了解相同的加数可以用乘法来计算，还应该对乘法的结构及意义进行深入的思考。如在教学中，应该渗透这里的相同的加数是3，有5个这样的加数，这样就形成一种新的思维路径。

这样增加一个思维点的价值是：

1. 实现加法算式与乘法算式的沟通。

虽然如上面例子中的加法算式可以写成两个乘法算式，但学生要明白这里相同的加数是“谁”，相同加数的个数是“谁”。这样学生说到“5个3”的时候，知道这里的每一份是3，有这样的5个3。也就是虽然我们不强调应该把相同的加数放在乘法算式前面的位置，但是我们要知道谁是相同加数，这样相同加数的个数有几个。其实这样一个过程就是把以乘法为背景的情境进行抽象，让学生借助乘法的背景更好地理解乘法的意义，从而为将来学生用乘法的意义解决实际问题提供了支撑。

2. 乘法模型的构建为结构化的认知提供支撑。

乘法学习的价值在于可以借助乘法解决生活中的许多问题，比如行程问题、植树问题、工效问题、价格问题等。在特定情境中，对相关术语的理解可以依托于乘法基本意义的理解。比如行程问题中的速度、时间和路程。这里的速度既是单位时间内走的长度，其实就是每份数，时间既是有这样的几份，就是份数。沟通了这样的联系，在乘法的意义的这部分教学就让学生对于相同加数及相同加数的个数有了清晰的认识，在今后的教学时，就可以借助这样的模型进行教学，形成结构化的统一体系，便于学生构建新知，形成对知识体系的清晰的理解和认识，降低学习的复杂性。

二、 关于乘法口诀学习过程中思维连续性的分析

在课例二中教者呈现一个比较乱的摆放的松果图，让学生思考“我”怎样能很快地知道一共有多少个松果。教者这样做的意图是什么？这里蕴含着什么样的思考？为什么教者强调让学生圈一圈、画一画？

1. 在真实的现实问题中思考。

人教版教材中给的一套福娃（图四），可以说蕴含了几个5的思考。那为什么教者给的是散乱的松果？笔者觉得这恰恰是教者还原真实的现实。我们在生活中数物体的个数的时候，物体多半处于零散的状态。在这种情况下，我们怎样处理呢？能直接用乘法？恐怕是不能的，这里必须有一个思维过程，就是分，而且是等分，实际上学生遇到这个问题的时候往往不是分成10个一组，因为这样对于他们来说每一份比较多。他们往往选择的是5个一组，比较好分，也比较好数。教者创造这样一个情境就是还原现实情境，让学生经历画一画、圈一圈的过程，感受思维连续性的发展过程，获得活动的良好经历和体验。

尤其这里渗透一个解决数学问题的策略就是“寻求同一性”，即如果面对比较复杂的问题，我们怎样把比较复杂的数据或问题变成“单一数据”或“单一情境”，通过简化问题，最后寻求问题的解决，这样的简单的处理是对学生思维方式和习惯的引领。

2. 关于乘法本质的实践性认识。

看似简单的圈一圈，我们发现这恰恰是乘法本质的实践性认识，就是加法与乘法的不同之处是什么。可能大家说，加法是加数不多，而且加数都不相同；乘法是加数都相同，或可以创造出相同加数。其实，笔者觉得可以再深入思考下，加法是相同计数单位的累积和叠加。如23+35，2个十与3个十的叠加，3个一与5个一的叠加。乘法是在计数单位的基础上进行拓展，可以若干个“标准”为基数的累积和叠加，如案例二中，就是5个为基数，1个5，2个5……若以计数单位累积的话比较容易计算，如几个1就是几，几个十就是几十。若以非计数单位累积和叠加，就非常不好计算，乘法口诀恰恰为这个过程提供了支撑，这也恰恰是乘法口诀学习的价值所在。

看似一个简单的处理，里面浓缩着教者对课程的理解及教材本质的认识和分析。所以，我们也经常说对教材的处理要深入浅出，就是对教材本质要有深入的认识，又要在课堂呈现上有一个简单的载体去呈现，使学生能够通过这样的环节对知识有深入的认识，从而为后续的学习提供强有力的支撑。

三、 关于乘法的运用过程中思维轨迹的分析

在课例三中，我们看到教师创设了一个情境，让学生在情境中运用所学的知识来解决问题，那从提取情境中的數学信息到运用所学的乘法知识来解决问题的过程中，我们潜藏的思维路径是什么呢？在思维的过程中怎样把“隐形”的思维显性化呢？

1. 让数形结合成为显性化的手段。

借助“数形结合”，让学生的思考及对问题的认识清晰化。如在课例三中让学生的每一次思考都要有形的助力。

让学生动手、动脑把“形的个数”借助“数”来抽象表达，把问题的解决，借助“形”来支撑。让学生在形与数的相互借力中完成对问题的解决，也让学生的思维在多种方式的表达中清晰呈现。

2. 借助语言的描述让思维清晰化。

在学习过程中让学生思维清晰化、条理化的另一个重要策略就是让学生学会用语言来表达数学。我们经常会发现一个现象，就是随着年龄的增长，想表达的学生越来越少，更有一个现象就是当我们让学生提出问题的时候，学生多半说不清楚、说不出来。

让学生用自己的语言来表达数学是非常有价值的，我们说思维是隐形的，如何让思维显性化，那就需要语言作为思维的载体，通过语言的表达让思维过程彰显出来。让学生用语言表达思维的过程是让他组织自己的语言，捋顺自己的思维，以期通过有理有据的表达让他人能听清楚，久而久之就会形成一种有条理的思维习惯，从而变成一种能力。这种思维的条理性、清晰性、外显性是学生数学核心素养的综合体现。

我觉得让学生能说、善说需要有相应的训练。对学生的表达训练需要阶段性，敢说——想说——会说——善说。

敢说——在学生最开始学习的时候，就让他能够安全地去表达，让他知道，只要他表达就会得到教师的欣赏，为他的敢说提供一种生态氛围。

想说——多利用赞赏的评价方式给予及时的鼓励，同时采用多种方式鼓励学生参与到说的过程中，通过小组互说做好准备，再到群体中分享，让他养成先准备充分，再积极表达的意识。

会说——教师的及时指导对于学生正确的表达非常重要。对于在发言过程中能有自己个性思考，对发言过程中能够针对问题集中研究，关注点清晰准确的学生及时鼓励。并对哪些观点和方法好给予提炼，给他们一个正确的导向，让他们学会如何去表达。

善说——教师从学生说的层次、说的方法上进行指导的同时，也可以教会他们在说的过程中借助某种方法和策略，比如上面提到的数形结合、举例说明等等。

学生在年纪小的时候，就潜移默化地开始训练，这样就可以渐渐形成会说的能力，能清晰表达“我”想的是什么，“我”什么没有弄懂，就不会进行“哑巴式学习”，提不出自己的问题和观点，也会让教师在他的表述过程中看到他思维的痕迹，使之成为教育的起点，真正为学生提供有效教学的基本素材。

3. 解决问题策略的多样性的共性提炼。

在上面课例中，教师提供学生学习的情境，并让学生多样化的表达，在这个多样化表达之后，教师经常少做一件事，就是共性和个性的对比分析。如在上面学生回答了多种方法之后，教师要引导学生思考，适时提出问题，这些方法之间有什么联系和区别呢？实际这里的联系就是在情境中寻找相同的每份（如图五）。如果图中物品的数量太多，直接数比较困难，我们就可以把图中的物品进行分割，分割成若干份，每一份都一样多问题就比较好解决了。分割的过程就是创造用乘法来解决问题的机会。分割后，我们只要数出有一份是几，有几份就可以用乘法来解决。

在上述方法进行对比后，我们还能发现在分割的过程中解决问题的共性都是找到每份和份数，但是不同点就是思考问题的方式分成两大类，一个是“余”，一个是“补”。在对比的过程中学生对于解决问题的方法就有一个比较清晰的认识。

这个比较的过程，就是结构化认知的过程。学生在知识点相互勾连的过程中，把握知识的核心和本质，让解决问题的方法、策略和经验与原有的认知结构发生联系，从而变成学生个体的经验和感悟，从而成为他们的素养和能力。

编辑/魏继军