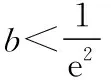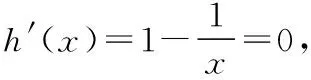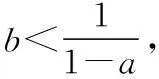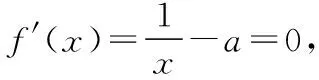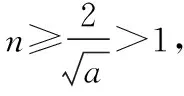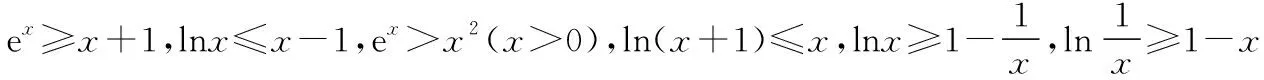巧借重要不等式,解一类零点问题
福建 黄清波
2017年高考数学全国卷Ⅰ理科第21题是一道函数与导数综合的压轴题,这类问题含有参数从而使得要解决的问题处于动态变化之中,这对考生分析应用知识、寻找合理的运算策略以及推理论证能力提出较高要求,多数考生“能懂会做”,但“对而不全”.为此,笔者进行了解题研究,探寻解题关键.
一、试题再现
【题目】已知函数f(x)=ae2x+(a-2)ex-x.
(1)讨论f(x)的单调性;
(2)若f(x)有两个零点,求a的取值范围.
【解析】(1)利用导数知识,易得当a≤0时,f(x)在R上单调递减;
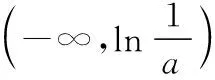
(2)(ⅰ)若a≤0,由(1)知,f(x)至多一个零点.
(ⅱ)若a>0,由(1)知,
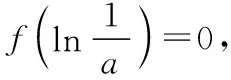
故f(x)只有一个零点;
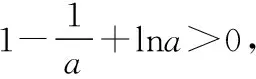
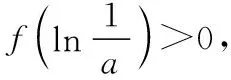
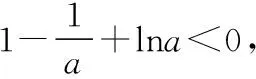
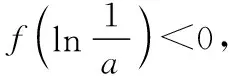
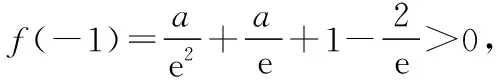
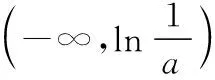
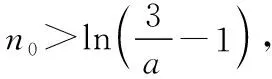
则f(n0)=en0(aen0+a-2)-n0>en0-n0>2n0-n0>0.
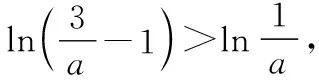
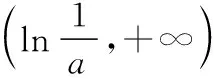
综上,0 在《普通高中课程标准试验教科书·数学2-2(选修)》(人教A版)习题1.3的B组第1题(3),利用函数单调性,证明不等式ex>x+1(x≠0).其进一步变形可得x>ln(x+1),x-1>lnx等很多新的结论. 若n-2≥1,(n-2)·x-lnx≥x-lnx≥1. 所以我们只要考虑n-2≥1,即n≥3. (1)讨论函数f(x)的单调性; (2)若函数f(x)有两个零点,求实数a的取值范围. 【解析】(1)利用导数知识,易得当a≤0时, f′(x)<0,f(x)在(0,+∞)上单调递减; (2)由(1)知,当a≤0时,f(x)在(0,+∞)上单调递减,故f(x)在R上至多一个零点,不满足条件. 则g(a)在(0,+∞)上单调递增,令g(a)=0,得a=e3, 故当0 当a=e3时,g(a)=0; 当a>e3时,g(a)>0. 若a>e3,则f(x)min=g(a)>0, 故f(x)>0恒成立,f(x)无零点,不满足条件. 若a=e3,则f(x)min=0, 令h(x)=(x-1)-lnx,x>0. 所以h(x)≥h(1)=0,即(x-1)-lnx≥0, 故x-lnx≥1. 综上,若0 综上,所求实数a的取值范围是(0,e3). 【变式2】(2013·江苏卷·20)设函数f(x)=lnx-ax,g(x)=ex-ax,其中a为实数. (Ⅰ)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围; (Ⅱ)若g(x)在(-1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论. 【解析】(Ⅰ)略. (Ⅱ)由于g(x)在(-1,+∞)上是单调增函数,解得a≤e-1. ①当a=0或a=e-1时,容易证明函数f(x)的零点个数为1; ②当a<0时,f(1)=-a>0,先证明lnx-x+1≤0(证略). 则f(b)=lnb-ab=lnb-b+1+(1-a)b-1<(1-a)b-1<0. 所以f(x)在(b,1)上存在零点. 又f(x)在(0,+∞)上单调递增, 所以函数f(x)在(0,+∞)上只有一个零点. ③当0 当x∈(0,a-1)时,f′(x)>0, 当x∈(a-1,+∞)时,f′(x)<0. 又a-1>e,所以f(a-1)=lna-1-a·a-1=lna-1-1>0. 由f(1)=-a<0,所以f(x)在(1,a-1)上存在零点,又f(x)在(0,a-1)上单调递增. 所以f(x)在(0,a-1)上只有一个零点. 下面考虑f(x)在(a-1,+∞)上的情况,需证明不等式ex>x2(x>e). 令h(x)=ex-x2,则h′(x)=ex-2x, 再设l(x)=h′(x)=ex-2x,则l′(x)=ex-2. 当x>1时,l′(x)=ex-2>e-2>0, 所以l(x)=h′(x)在(1,+∞)上单调递增. h′(x)=ex-2x>e-2>0, 所以h(x)在(1,+∞)上单调递增. h(x)=ex-x2>e-1>0,所以,当x>e时,ex>x2, 又因为a-1>e,所以a-2-ea-1<0. 取一个正数m=ea-1>a-1, 则f(m)=f(ea-1)=lnea-1-a·ea-1=a(a-2-ea-1)<0. 所以f(x)在(a-1,+∞)上存在零点, 又f(x)在(a-1,+∞)上单调递减. 所以f(x)在(a-1,+∞)上只有一个零点. 综上,当a≤0或a=e-1时,f(x)的零点个数为1; 当0二、存在困惑
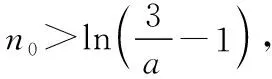
三、释疑解惑
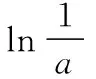
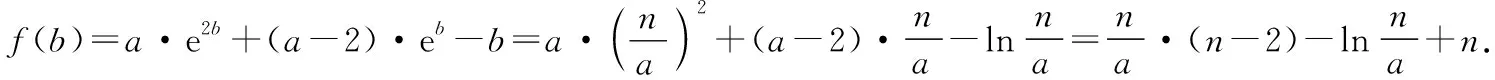
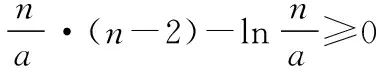
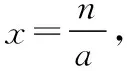
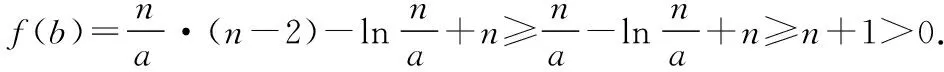
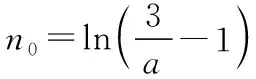
四、内化应用