由“重心”引发的思考谈起

陕西 吕二动

我们在数学必修四所学的平面向量中有这样一道试题：

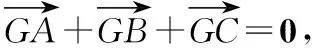
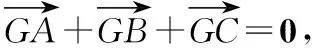
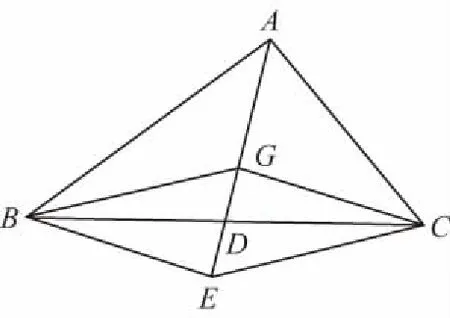
以GB，GC为邻边作平行四边形GBEC，GE交BC于点D，

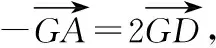
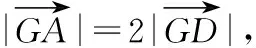
∴G为△ABC的重心．

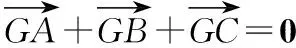
一、命题研究

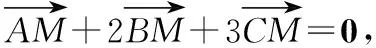
解法一：取CB，CA的中点D，E.

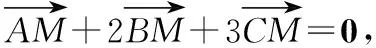
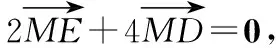
∴M,D,E三点共线.

又因为D,E分别为CB，CA的中点，

∴DE

∴M为CN的中点，

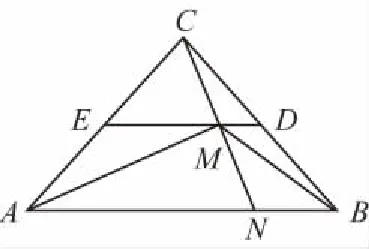
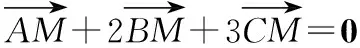
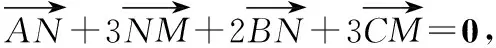
又∵A,N,B三点共线，C,M,N三点共线，

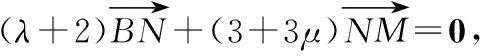
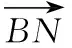
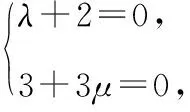
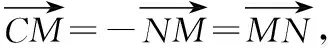
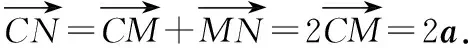
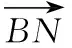
推论1：e1和e2是同一平面内两个不共线的向量，若存在实数λ1,λ2，使得λ1e1+λ2e2=0，则λ1=λ2=0．

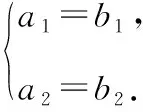
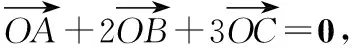
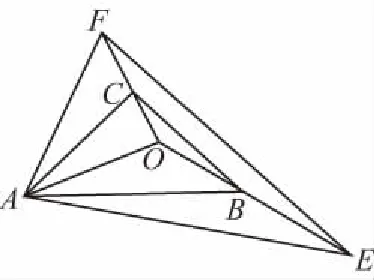
解法一：如图，设D，E分别是AC，BC边的中点，

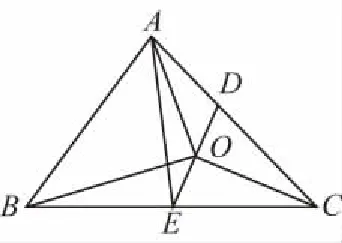
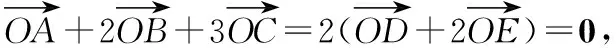
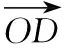
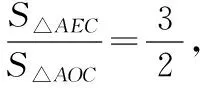
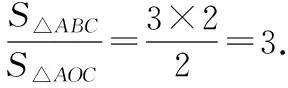
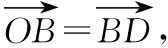
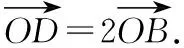
连接AD，以OA，OD为邻边作平行四边形，

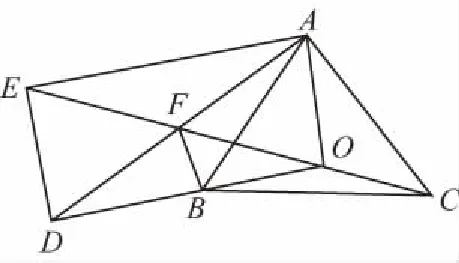
∴C，O，E三点共线，∴OE=3OC，

∴S△AOE=3S△AOC=S△DOE，

∵BF

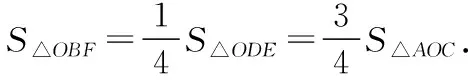
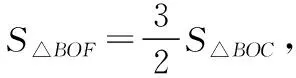
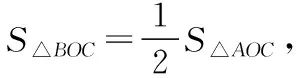
∴S△ABC=S△AOC+S△AOB+S△BOC=3S△AOC，

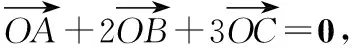
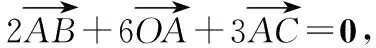
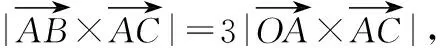
∴S△ABC=3S△AOC，

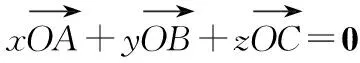
二、命题推广

可将变式2进行推广：

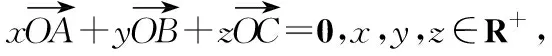
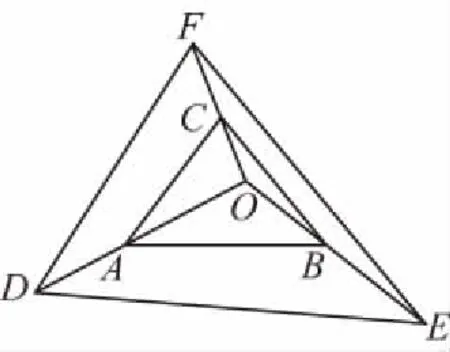
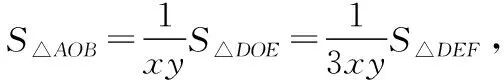
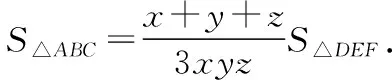
下面来看此公式的逆用：

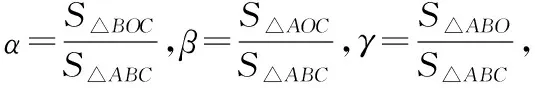
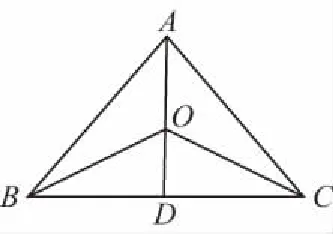
证明：如图，延长AO交BC于D，

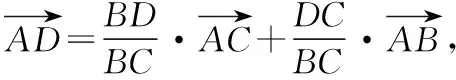
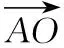
由α+β+γ=1，故上式可变为

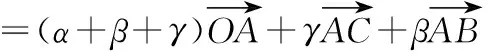
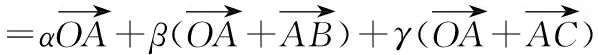
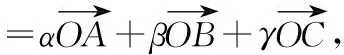
我们可以将问题推广至三维空间：

推广3：点P是四面体A-BCD内部一点，若VA-BCD=V，

VP-BCD=VA,VP-CDA=VB,VP-ABD=VC,VP-ABC=VD,

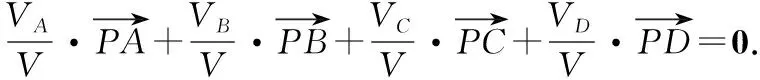
在证明之前，我们先来看一个简单的引理：

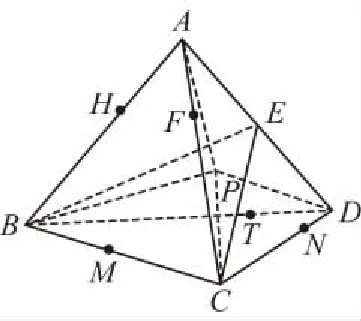
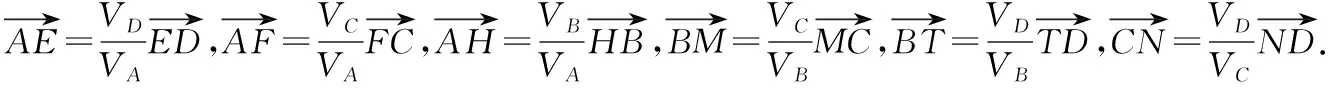
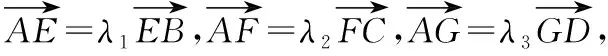
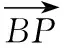
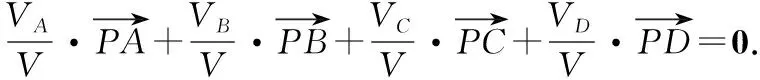
当然，还可以推导点P在△ABC及四面体A-BCD外部的不同位置时的类似关系式，这一点留给有兴趣的读者探讨.