平台自标定技术综述

王 琪，汪立新

（火箭军工程大学，西安710025）

0 引言

系统误差分析结果表明：平台系统中，陀螺仪、加速度计的误差是制导工具误差的主要误差源。因此在使用前对陀螺仪和加速度计的误差项进行标定和补偿，能够有效地提高平台的精度。实践表明，陀螺仪长期稳定性测试中（多次启动）的随机量与一次启动的随机量相比相差较大。如在3个月稳定性测试中，陀螺仪一次项漂移的随机最大约为 0.05（°）/（h·g），零次项的随机量约为0.03（°）/h。而一次启动时，陀螺仪一次项的随机量约为 0.01（°）/（h·g），而零次项的随机量约为0.001（°）/h。加速度计的标度系数及零次项，逐次启动之间也有差异。显然，对陀螺仪漂移均值进行补偿后，利用陀螺仪一次启动随机量小的特性和射前装订加速度计标度系数的实测值，将会提高导弹的命中准确度。因此，提出对平台系统进行射前自标定。

陀螺仪平台射前自标定，就是对陀螺仪和加速度计进行射前测试，再用最小二乘法进行数据处理，得到陀螺仪各项漂移系数和加速度计的零次项，将其送入弹上计算机进行补偿，分离出加速度计的标度系数送入弹上计算机进行装定[1]。

国外技术先进国家大多采用射前自标定技术大幅提高了导弹武器系统的制导精度，用一次稳定性代替逐次稳定性，减小随机误差，在导弹和火箭发射前对平台进行一次通电的误差模型现场标定，经过数据处理后分离出各项误差系数传给制导计算机，进行实时补偿[2-4]。美国在20世纪40年代已经开始致力于惯导设备及器件的相关研究，美国的MX导弹平台系统在常备热待命状态下采用连续翻滚方法进行不间断自标定，标定参数达到86项，民兵III等战略导弹也采用类似的常备自标定技术[5]。俄罗斯的 “白杨系列”导弹也采用射前自标定技术，分离误差系数多达70余项[6]。

平台误差系数标定主要可以分为两大类方法：多位置自标定和连续旋转自标定。而多位置自标定中根据产生标定位置的机理不同，又可分为力反馈单表测试法、多位置闭路反馈测试法和多位置开路测漂法[7]。国内研制单位一般采用多位置闭路反馈测试法和多位置开路测漂法进行自标定，国外高精度平台系统一般采用连续翻滚标定法进行自标定[8]。

1 多位置自标定

1.1 多位置自标定原理

平台多位置自标定是将平台坐标系进行多位置自动翻滚，若被测轴需沿地垂线朝上朝下处锁定测漂及测量加速度计输出状态，则平台另外两个轴处在调平状态。若被测轴处在水平状态，则先两轴调平另一轴锁定，然后断开被测轴调平自动转入锁定测漂状态。这种自标定方法可同时确定出陀螺仪和加速度计的有关参数[1]。平台多位置自标定的原理可以简介如下。

在重力场内，若忽略二次项，陀螺仪误差模型可简化为：

式中，D0为零次项漂移，单位为[（°）/h]；DI、Ds分别为沿陀螺仪输入轴和马达轴的一次项漂移系数，单位为[（°）/（h·g）]。

若忽略二次项，加速度计的数学模型可表示为：

式中，E0为加速度计的零次项，A1为加速度计标度因数。

在测试时，根据需要标定的参数数目，使平台坐标系处于不同的位置，获得不同位置下的陀螺仪和加速度计的输出，根据式（1）和式（2）运用最小二乘法或其他参数辨识方法就可以得到陀螺仪和加速度计的误差系数。

平台误差自标定方法有多种，应根据需要标定的参数数目、标定精度的要求、平台的结构形式、标定时间确定其方法。徐军辉等[9]对有限转动导航平台的自标定进行研究，有限转动导航平台的自标定主要是依靠平台的自身条件和特性来完成误差系数的标定和分离，而并不依靠任何外部转台。陀螺仪采用九位置标定法，加速度计采用五位置标定法。该方法有助于缩短平台的测试时间，提高武器系统的使用精度。杨立溪[10]针对一种三轴平台设计了1个十六位置误差标定及自主对准一体化方案，可以分离出总计42项误差，其中包括自主确定方位。肖正林等[11]提出了1种总误差标定及方位对准采用导弹水平状态七位置一体化方案，在约13.6min内能自主对准并标定出平台21项系数。导弹水平状态标定与对准可以基本消除阵风干扰的影响，且陀螺仪标度因数与漂移的估计采用有参考力矩的零力矩法，保证了标定、对准的快速性与准确性。

平台多位置自标定须要解决3个问题：陀螺仪和加速度计误差模型建立、标定位置选择和参数辨识方法。

1.2 陀螺仪和加速度计误差模型

从平台多位置自标定的原理可以看出，陀螺仪和加速度计的误差模型（式（1）和式（2））的准确性对误差标定结果的准确性起着决定性的作用，误差模型建立得越精确，标定结果的精度就越高。

在最初的平台误差模型中，人们仅仅考虑的陀螺仪误差系数和平台漂移之间的关系，所用的陀螺仪漂移模型大多比较简单，仅仅包含陀螺仪和加速度计的零次项和一次项误差系数。而研究表明，在多位置自标定中，框架轴安装误差与角度传感器误差对误差系数的标定精度影响很大，特别是对陀螺仪与加速度计安装误差的标定，影响非常显著[12]。后来从平台系统的角度出发，将加速度计的误差系数、仪表的安装误差、平台的初始对准误差、稳定回路的传递误差、数字化的量化误差等因素都纳入了平台的误差模型当中，并对部分随机误差进行了分类研究[2，13-14]。Bar-Itzhack等提出了一种比较理想的静基座下的惯导系统误差模型，指出可采用一种线性变换，在初始对准和标定阶段将误差模型的状态矢量变换为速率状态矢量，它从新的动态矩阵观测到的速率状态矢量可分成彼此完全解祸的可观测和不可观测部分，这就免除了确定系统不可观测空间的繁冗的经典算法[15]。Goshen-Meskin等提出了推导惯导系统误差模型的统一方法，这个方法说明可以用几条扰动规则、导航变量、误差变量、参数坐标及实现线性化坐标系等几种选择求出现有的误差模型[16]。在此基础上Weinreb等[17]、Yu等[18]、Robert等[19]、Thompson等[20]针对不同应用背景推导了惯性系统误差模型。

国内对于平台多位置自标定的模型建立也越来越完善，但是仍存在一些不足。刘西河等[21]讨论了一种可以标定54项误差系数的多位置自标定方法，但未涉及加速度计和陀螺仪的安装误差。文献[22]～文献[24]虽然给出了陀螺仪和加速度计安装误差的标定方案，但未能标定陀螺仪全部的二次项误差系数和加速度计的二次误差系数，也就是标定的误差系数不够多。因此下一步应该继续提高模型的精确度，从而提高误差标定精度。

1.3 标定位置选择

标定位置的选择是平台多位置自标定的决定性因素之一，因为位置组合的选择会直接影响误差系数标定的个数和精度，好的标定位置组合既能够提高标定精度，同时又能够减少标定时间。然而由于误差模型建立得越来越复杂，位置组合的选择逐渐转变为一个很困难的非线性优化问题，国内外研究位置选择的还比较少，甚至是回避此问题，目前多位置自标定中位置选择主要依靠工程经验。

包为民等[25]给出了一种最优多位置组合的实验方法，分析了位置选择对自标定精度的影响，设计了一种十六位置标定方案。孟卫锋等[26]分析了系统观测矩阵和信息矩阵的特征，通过使观测矩阵的条件数最小这一优化指标得出最佳位置组合选择算法，并在此算法基础上得出一种十六位置标定方案。总的来说，目前对于标定位置选择的研究还比较少，下一步需要继续深入研究。

1.4 参数辨识方法

在最初的平台多位置自标定中，由于陀螺仪和加速度计误差模型中只考虑了零次项和一次项，是一个线性模型，因此一般利用最小二乘法进行参数辨识。但随着误差模型建立得越来越完善和复杂，非线性项越来越多，现在更多的利用非线性参数辨识方法，其中最多的是非线性最小二乘法和非线性Kalman滤波方法。

吴成迈等[27]研究了自适应滤波算法在平台自标定数据处理中的应用。利用常角速度模型，对角度传感器输出采样建模，把漂移角速度设为一个状态变量，采用参数辨识的方法来解算漂移角速度。仿真表明，采用自适应Kalman滤波能较好地满足定标精度要求，这种技术已经广泛应用到各个领域中去了。王跃钢[28]针对阵风干扰对标定精度影响很大的情况，设计了小波滤波加分组拟合加权平均算法。在使用小波滤波器对数据滤波后，采用分组拟合加权平均算法辨识漂移角速度，在此基础上解算漂移参数。结果表明，动基座基本上与静基座试验结果的误差水平相当。唐江河等[29]考虑到利用EKF辨识包含陀螺仪交叉项的参数时存在难以收敛甚至有些参数出现发散的问题，提出了分步辨识的方法来解决这一问题。目前看来，由于陀螺仪和加速度计误差模型的非线性程度不高，已有的非线性参数辨识方法已经可以很好地解决这个问题。

1.5 多位置自标定存在的不足

到目前为止，多位置自标定技术已经发展得比较成熟，在实际中特别是国外已得到了广泛应用，但是也存在以下几点缺陷：

1）多位置自标定需要一定的外部设备（如精密转台）来使平台满足多位置的条件，对操作造成了不便。

2）多位置自标定中标定精度和标定速度是一对矛盾的指标，为达到一定的标定精度，就需要设计更多的标定位置，从而降低标定速度，这样不能满足实际应用中快速标定的要求。因此，需要对多位置自标定的标定位置选择问题进行深入研究。

3）实践已经证明，多位置自标定中对于陀螺仪安装误差的表达精度很低，这是因为作为陀螺仪安装误差激励的地球自转角速度比较小，无法充分激励陀螺仪安装误差。若要进一步激励陀螺仪安装误差，需要对平台施加加矩角速度，这就引出了第二种平台误差系数标定方法——连续旋转自标定。

2 连续旋转自标定

2.1 连续旋转自标定原理

多位置自标定方法是一种 “静态”标定方法，需要精密转台等设备精确确定惯性系统三轴的空间指向，然后测量陀螺仪与加速度计在稳定状态下的输出，使用最小二乘或其他参数估计方法估计误差系数。连续自标定方法则是一种 “动态”标定方法，通过施加外部力矩使平台按照预先设定的轨迹连续转动，在转动状态下采样加速度计的输出，然后利用滤波等参数估计方法获得误差系数的估计。连续自标定方法不需要精密转台等设备，只需要对平台施加一定精度的外部力矩，驱动平台旋转，同时具有较高精度的角度测量传感器即可。

平台连续自标定技术的基本原理如下：惯性平台在外力矩的作用下以角速度ωc（称为加矩角速度）转动，在地球自转角速度、加矩角速度以及重力加速度的激励下，加速度计输出中包含有陀螺仪漂移、加速度计漂移、安装误差和平台对准误差等全部误差信息。以加速度计输出为观测量，以平台对准误差方程为动力学模型，采用最优滤波算法估计平台误差系数和对准误差，并用估计结果对平台模型进行补偿与调整。所以，连续自标定在完成平台误差标定的同时，还能够实现平台的对准[30]。

平台连续旋转自标定最早由Jackson[31]于1973年提出，他利用连续自标定方法获得了Peacekeeper导弹平台误差系数的估计，但是文献[31]中将连续自标定系统模型简化为线性模型，而且从该文献看，其参数估计并不准确，无法满足高精度补偿要求。

有关资料显示，连续旋转自标定已经在国外发展成熟并得到了实际应用[5，8，32]。但是由于保密和技术限制等原因，关于连续旋转自标定的国外文献较少。国内对于连续旋转自标定的研究目前刚刚起步，相关文献比较少。杨华波[30]在其博士学位论文中，首次比较系统地介绍了连续旋转自标定的模型建立、可观测性分析、旋转方案设计和参数辨识。针对失准角误差模型，不仅引入了小角度线性假设误差，而且对推导框架角输出漂移模型带来了较大困难的问题。曹渊等[33-34]建立了基于框架角动力学方程的平台连续翻滚模型，利用Lie导数及输出灵敏度理论全面分析了连续翻滚路径下惯导系统的可观测性，提出了一种结合传统多位置试验的平台连续翻滚自标定方案。连丁磊等[35]针对惯性平台误差标定建模问题进行了研究，详细分析了陀螺仪安装误差和加速度计安装误差对导航结果的影响，建立了基于陀螺仪敏感轴系基准的平台自标定模型。该模型以陀螺仪敏感轴为基础定义了平台坐标系，以该坐标系为基准，陀螺仪的安装误差角由9个减少到3个，加速度计安装误差由9个减少到6个，降低了模型的复杂程度。针对浮球式惯性平台系统的标定与初始对准问题，丁智坚等[36]提出了一种基于姿态角的连续翻滚自标定自对准方法，该方法可以同时实现平台系统42项误差系数的高精度标定与初始对准。但是由于目前国内能够满足连续旋转自标定的全姿态平台较少，因此目前大多数研究都还只是停留在系统仿真阶段，缺乏试验验证。

目前，连续旋转自标定的研究主要存在两个难点：误差模型建立和系统可观测性分析。

2.2 误差模型建立

根据状态量选择的不同，连续旋转自标定主要有两种误差模型：失准角误差模型和框架角误差模型。其中，失准角误差模型的基础是基于失准角的姿态误差方程[8]：

式中，φ为失准角，ωIp为平台相对于惯性空间的转动角速度，ε为陀螺仪误差引起的平台漂移。

框架角误差模型的基础是基于框架角的姿态误差方程[33]：

其中，T1＝，，α、β、γ为3个平台框架姿态角，为平台相对于惯性空间的转动角速度，ωp0为平台基座相对于惯性空间的转动角速度。

然后将失准角、陀螺仪误差系数、安装误差、加速度计误差系数、安装误差增广为状态向量，代入式（3）和式（4），以加速度计误差方程为观测方程，就可以得到连续旋转自标定系统的状态空间表示。

目前的难点在于如何精确地确定ωIp、ε、的表达式，这对于模型的精确度有着巨大的影响，从而影响最后的误差标定精度。因此需要对平台的误差传播机理进行深入分析，得到尽可能精确的误差模型。

2.3 系统可观测性分析

由于连续旋转自标定是一个时变非线性系统，要对其参数进行辨识，系统可观测性分析是非常重要的一个前提。对于状态空间模型而言，系统的可观测性分析方法非常多，如针对线性定常系统的Lyapunov方法[37]、奇异值判断方法[38]等。对于线性时变系统，由于参数随时间变化，有限个时间点下系统的可观测性不能作为连续系统可观测性的充分条件。传统的Lyapunov方法是将可观测性矩阵从初始时刻积分到给定时刻，然后判断参数化可观测性矩阵的秩，以此来确定系统可观测性，这种方法的主要困难在于计算的可行性，特别是对于高维问题，这种计算几乎是不可能的。针对这一困难，Goshen-Meskin等[39-40]提出了一种针对线性时变系统的可观测性方法，这种方法将线性时变系统假设为分段的定常系统（Piece-Wise Constant Systems，PWCS），根据线性定常系统方法求出每一段的可观测性矩阵，Goshen-Meskin与Bar-itzhack证明局部可观测性矩阵的秩与系统总的可观测性矩阵的秩是等价的，因此可利用局部可观测性矩阵分析系统的可观测性，这种分析方法广泛应用于惯性系统的初始对准问题中。

但是对于非线性时变系统，线性系统可观测性分析方法失效，此时可使用Lie导数分析方法。Taur等[41]利用Lie导数分析方法分析了地空反导导弹复合制导系统的可观测性问题，Zhu等[42]利用Lie导数分析了目标跟踪中的可观测性问题，取得了不错的效果。

Lie导数可以分析非线性系统的可观测性，但是随着状态变量维数的增加，Lie导数方法的运算量会急剧增加。而且Lie导数只能分析系统整体的可观测性，对于具体的每一个参数的可观测性则无能为力，而这对于旋转方案的设计至关重要。所以有必要对每个参数的可观测性进行定量描述，即可观测度。杨晓霞等[43]对已有的两种可观测度分析方法进行了简述，并且分析了两种方法的等价性，然后从理论上分析了此描述方法的不全面性。通过典型例子说明了理论分析的结果，给出了一种更全面的描述系统可观测组合状态可观测度的方法，并且用新的描述方式分析了捷联惯导系统的各状态可观测度。刘准等[44]提出了一种使用条件数来定量分析系统可观测性的新方法，该方法克服了传统可观测分析方法不能定量地分析系统可观测性的缺点，它不仅可以定量地时不变系统的可观测性，而且通过多量测估计和构建局部可观测矩阵的方法，还可以定量地分析时变系统在任意时间段内的可观测性能。许永飞等[45]利用输出灵敏度理论分析了连续旋转自标定系统的可观性，指出加速度计安装误差可观性较差是影响标定精度的主要原因，性差是由安装误差之间的线性相关性造成的，并确定了具体的不可观参数。以加速度计输入轴为基准建立平台坐标系可以减少安装误差项，使所有的安装误差变得可观。上述文献都是利用系统的某一种定量指标来描述可观测性，但是由于只有仿真实验结果，缺乏试验验证，方法缺乏说服力。

2.4 连续旋转自标定有待解决的问题

连续旋转自标定由于操作简单，不需要外部设备，相对于多位置自标定具有先天的优势，但是还有几个有待解决的问题：

1）对于平台误差模型的认识还不够深刻，建立的模型与实际情况存在偏差，导致滤波效果不好；

2）时变非线性系统特别是具体参数的可观测性分析没有系统可靠的方法，虽然已有论文对此方面进行了研究，但都是间接分析参数可观测性，而并没有有效的方法可以直接进行分析；

3）目前国内缺少可以用于试验验证的全姿态平台，目前国内这方面的研究都还停留在仿真阶段。

3 平台自标定技术研究展望

根据前两节对两种标定方法的介绍，对两种方法进行比较，如表1所示。

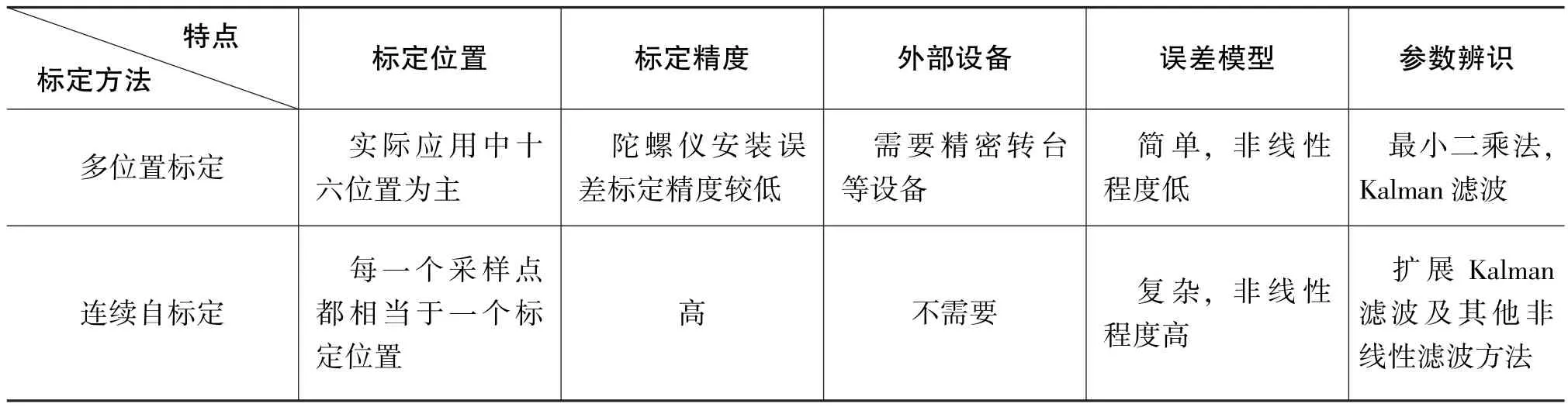
表1 两种标定方法比较Table 1 Comparison of two kinds of calibration methods

由于平台自标定技术对提高制导武器精度有着巨大作用，一直以来都是一个研究重点。目前看来，多位置自标定技术已经发展得比较成熟，也得到了实际应用。但是由于多位置自标定存在依靠外部设备、对安装误差标定精度不高等问题，已经渐渐不能满足高精度、快速性、装机自标定等要求，因此有必要研究连续旋转自标定。

连续旋转自标定由于其便捷性、快速性等优点，已经在国外的高精度平台系统上得到了应用，并且有很好的效果。国内由于起步较晚，目前在该技术上与国外还有较大差距，目前主要存在误差模型建立、可观测性分析和试验验证这3个问题。若能解决这些问题，对于提高制导武器精度将起到重要意义。