单轴旋转捷联惯导系统误差分析与转位方案

石潇竹，胡 杰

（1.空中交通管理系统与技术国家重点实验室，南京210007；2.中国电子科技集团公司第二十八研究所，南京210007）

0 引言

光纤陀螺是一种无机械转动的全固态陀螺，被广泛应用于捷联惯导系统（SINS）中[1]。光纤陀螺的常值漂移是引起惯导系统导航误差的主要因素，需要采用相关技术予以补偿，旋转调制技术是SINS中一种常用的误差自校准方法，可以在不使用外部信息的情况下，通过对惯性测量单元（Inertial Measurement Unit，IMU）周期性转动以调制IMU的常值误差，减小对系统精度影响[2]。美国在20世纪70年代开始了此类系统的研究，典型的研究成果有MK39Mod3C、WSN-7B单轴旋转系统，MK49、WSN-7A双轴旋转系统以及ADMII、ADMIII三轴旋转系统。目前，国外的单轴、双轴旋转式惯导系统已经在国内得到应用，三轴旋转惯导系统也已经完成各项验证实验，并有望替代静电陀螺平台式惯导系统应用于核潜艇[3-5]。

近年来，国内许多研究机构也展开了旋转式惯导系统的研究工作[6-9]。文献[6]分析了单轴旋转惯导系统自补偿基本原理，对影响旋转调制效果的各项误差进行了研究。文献[7]分析了IMU误差模型和旋转式捷联系统误差传播方程，设计了单轴正反转停和双轴转位的系统旋转方案，并进行了相应的数学仿真。文献[8]提出了一种带倾斜转位机构的单轴旋转调制方案，将IMU放置一定的倾斜角度可以消除转轴方向上陀螺常值漂移误差对导航精度的影响，其定位精度与双轴旋转惯导系统相当。上述文献对旋转调制误差补偿的原理都做了详细的研究，但对系统的旋转方式以及工程适用性缺少必要的研究与说明。本文在对IMU误差调制机理分析基础上，给出了单轴单向连续旋转、两位置正反转停（大于360°）、四位置正反转停（小于360°）3种旋转方式，对不同旋转方案的误差调制效果进行了分析与研究，并在单轴旋转惯导系统上进行了验证实验。

1 旋转调制原理

传统的SINS中，IMU直接与载体固连，它们之间没有相对运动。旋转式SINS中，IMU安装在转位机构上，导航计算机控制转位机构使其做周期性转动。本文中的IMU由3个光纤陀螺和3个石英挠性加速度计正交安装组成，旋转机构具有绕天向轴单轴旋转功能，IMU固连在旋转机构上。

定义：s系为旋转坐标系，b系为载体坐标系，n系为导航坐标系，i系为惯性坐标系，初始时刻s系与b系重合。

单轴旋转惯导系统中，IMU绕ozb连续旋转，在t时刻旋转角速度为Ω，b系相对s系的变换矩阵为：

在旋转式SINS中，考虑标度因数误差与安装误差，陀螺和加速度计输出误差为：

式中，Kg、Ka为陀螺和加速度计的标度因数误差阵，θg、θa为陀螺和加速度计安装误差阵，Bg为陀螺常值漂移，Ba为加速度计常值偏置，δω、δf为陀螺和加速度计随机误差。

根据式（1），可以将陀螺和加速度计输出误差由旋转坐标系s转换到载体坐标系b：

由式（3）可以看出，IMU经过周期性转动后，x轴和y轴惯性元件的常值误差，呈现周期性变化，一个积分周期内其误差为0，z轴误差没有变化。

2 旋转式捷联惯导系统误差调制机理分析

考虑标度因数误差以及安装误差，陀螺组合件误差模型可写成：

ω，Bg和δω分别表示陀螺一次启动常值漂移与随机噪声误差。

2.1 标度因数误差旋转调制分析

当只考虑标度因数误差时，陀螺组合件误差为：

通过分析推导可得：

由式（6）可以看出，经过旋转调制后标度因数引起的水平方向误差依然存在直流分量，即单轴旋转调制对水平方向上的补偿作用有限，但在方位轴上引入了大小为KgzΩ的常值漂移。例如：当方位轴陀螺标度因数误差为1×10－5时，转位机构16（°）/s的转速将引入 0.576（°）/h 常值漂移，这对于高精度惯性导航系统是不可容忍的。为了避免转动引起的标度因数耦合误差，需要采取正反交替的旋转方式。

2.2 安装误差旋转调制分析

同理，只考虑安装误差时，式（4）可简化为：

通过分析推导可得：

式中，

由式（8）可以看出，经过旋转调制后，旋转轴方向上安装误差能够被调制，水平方向误差依然存在。

2.3 常值漂移误差旋转调制分析

当只考虑常值漂移误差时，陀螺组合件误差为：

当转轴做周期性旋转时，与转轴垂直平面上的常值误差被调制，而转轴上的陀螺常值误差没有补偿效果。等效北向陀螺常值漂移和天向陀螺常值漂移决定了系统最终的经度误差，单轴旋转调制系统中，水平方向上的陀螺常值漂移经过旋转调制后误差被抵消，所以系统能在一定程度上抑制经度误差的积累，提高了SINS的定位精度。

2.4 随机漂移误差旋转调制分析

陀螺随机漂移误差项Cbsδω均值为0，随机变量经过旋转调制后依然为随机变量，因此旋转调制对随机漂移没有调制作用。

加速度计组合件输出误差的调制结果与陀螺组合件输出误差的调制结果类似，具有相同的结论。

3 旋转方案设计

3.1 单轴单向连续旋转

单轴连续旋转调制系统描述如下：初始时刻s系与b系重合，启动上电后转位机构以一定的角加速度加速至角速度为Ω，然后转位机构一直以该恒定角速度连续旋转，直到导航系统关机停止工作为止。

3.2 大于360°两位置正反转停旋转

大于360°两位置正反转停旋转方案如图1所示，转动方案描述如下。

次序1：IMU从位置A点出发逆时针转180°到达位置B点，停止时间Ts；

次序2：IMU从位置B点出发顺时针转180°到达位置A点，停止时间Ts；

次序3：IMU从位置A点出发顺时针转180°到达位置B点，停止时间Ts；

次序4：IMU从位置B点出发逆时针转180°到达位置A点，停止时间Ts。

然后按照次序1～次序4的顺序循环运动，不同位置处停留5min。

3.3 小于360°四位置正反转停旋转

小于360°四位置正反转停旋转方案如图2所示，转动方案描述如下。次序1：IMU从位置A点逆时针转动180°到达位置C点，停止时间Ts；

次序2：IMU从位置C点逆时针转动90°到达位置D点，停止时间Ts；

次序3：IMU从位置D点顺时针转动180°到达位置B点，停止时间Ts；

次序4：IMU从位置B点顺时针转动90°到达位置A点，停止时间Ts；

然后按照次序1～次序4的顺序循环运动，不同位置处停留5min。

4 仿真研究

4.1 惯性器件参数设置

假设3个陀螺的常值漂移均为0.01（°）/h，随机游走系数为0.001（°）/h，标度因数误差为 1×10－5，陀螺组件的6个安装误差角为10″；3个加速度计的偏置均为100μg，随机白噪声标准差为200μg，标度因数误差为1×10－5，加速度计组件的6个安装误差角为10″；转位机构测角精度为5″。

4.2 载体运动参数设置

初始经度为 106.6906°，纬度为 26.5019°；系统模拟摇摆运动，姿态角变化规律分别为：俯仰角，横摇角，航向角

假设初始航向角误差为1′，初始俯仰角误差和横摇角误差均为15″，旋转机构测角误差为5″，陀螺和加速度计采样间隔时间为5ms，由于连续旋转方式不具有工程应用价值，这里仅对以下3种方案进行仿真，仿真时间设置为72h。

1）没有旋转；

2）大于 360°两位置正反转停旋转，转速为16（°）/s，每个位置停留时间为 5min；

3）小于 360°四位置正反转停旋转，转速为16（°）/s，每个位置停留时间为 5min。

图3给出了3种转位方式下的导航定位误差曲线。

由图3可以看出，两位置正反转停方案与四位置正反转停方案72h的定位精度相当，分别为18.37nmile和18.36nmile。而非旋转式 SINS中，同样的惯性器件误差条件下，其72h的定位误差为55.52nmile，这充分体现了旋转调制的作用，同时也说明了四位置转停方案与两位置转停方案具有同样的抑制导航误差性能。

5 实验及分析

利用实验室三轴转台、车载实验系统和自行研制的单轴旋转SINS进行验证实验，其中IMU由3个光纤陀螺与3个石英挠性加速度计组成。转台实验环境和车载实验环境分别如图4和图5所示，单轴旋转SINS的主要技术参数如表1所示。

在实验室环境下，转位机构转位方式采用四位置转停方案。四位置转停方案中采用的转位机构不需要导电滑环，因此具有更高的可靠性，产品上电后转位机构初始化使得载体坐标系b与旋转坐标系s重合。图6详细描述了惯导系统实验过程中各个时间段的工作状态，前3min进行粗对准，采用的是惯性系解析法[10]；然后进行精对准，精对准时间为20min，精对准结束后，转入到纯惯性导航工作模式。转台实验和车载实验分别进行了两组验证实验，其中一组实验转位机构停止旋转；另一组实验启动转位机构，进行误差调制。

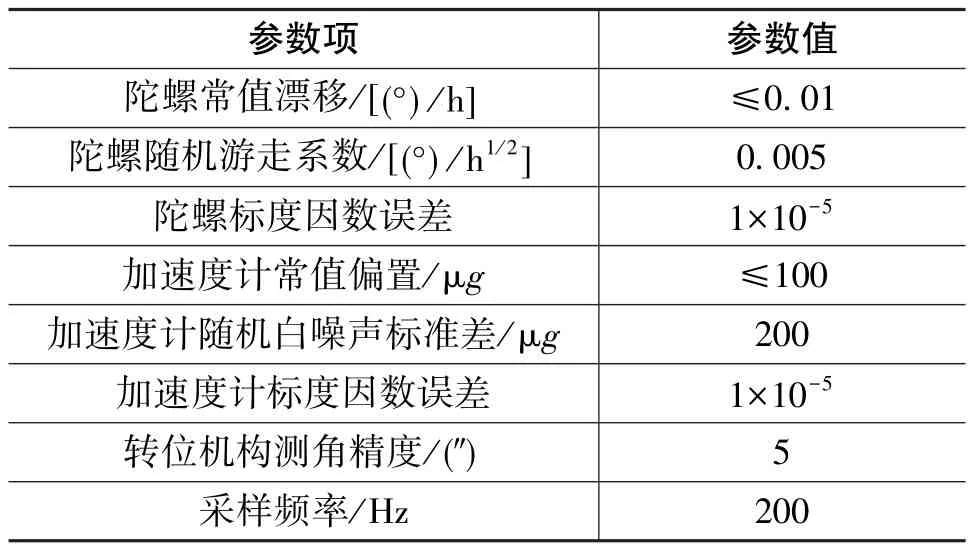
表1 单轴旋转捷联惯导技术参数Table 1 Specifications of the single-axis rotary SINS

图7为转台实验误差对比曲线，由图7可知，当系统IMU不进行旋转时，5h导航结束后的定位误差为1.98nmile。当IMU进行四位置转停旋转后，其5h导航结束后的定位误差为0.51nmile，说明了单轴旋转调制能够抵消IMU误差对系统精度的影响，提高了SINS的定位精度。

图8是某次车载实验路线图，在起始点先进行初始对准实验，对准结束后启动车辆开始实验。沿着路线以10km/h的车速到达某处调头继续行进到实验结束，验证实验共进行了5h。

由图9可知，系统不进行旋转调制导航时，5h内位置误差最大为2.2nmile。当采用四位置单轴旋转调制方案时，5h系统定位误差最大为0.81nmile，系统最终定位精度得到了很大的提高。

结合转台摇摆实验和车载环境动态实验定位误差结果可知：水平方向陀螺误差对定位精度的影响基本被调制，系统实验结果满足初始设计指标，可以为单轴旋转SINS的研制提供理论与实践指导。

6 结论

本文对旋转式SINS误差特性进行了分析，给出了旋转调制对陀螺标度因数误差、安装误差、常值漂移和随机误差的调制作用。单轴旋转调制能将与转轴垂直方向上的惯性器件的常值误差调制成周期性分量，通过积分运算，可以消除其对导航定位精度的影响。转轴方向上的标度因数误差会与旋转角速度相耦合，这样会进一步放大其对导航定位精度的影响，因此在工程应用中需要采取正反旋转的方案，以抵消该项误差。旋转调制对安装误差以及随机噪声误差的调制作用很小，高精度导航系统前期转台标定时应尽可能减小该项误差。

给出了单轴旋转SINS的3种常用转位方式，在数学仿真环境下对其中两种转位进行了仿真验证，指出两位置与四位置具有同样的旋转调制功能，但是四位置转停方式不需要滑环，工程应用中具有更高的可靠性。利用三轴摇摆转台、车载实验系统以及单轴旋转SINS进行了静态和动态验证实验，结果能够满足系统初始设计指标，具有工程参考价值。