正弦余弦算法优化的SVM模拟电路故障诊断

朱 静，何玉珠，崔唯佳

（1.成都航空职业技术学院，成都610100；2.北京航空航天大学仪器科学与光电工程学院，北京100191）

0 引言

在武器系统、航空航天等国防军工领域，对电子设备的指标要求更加苛刻，对自动化的故障诊断和先进的故障诊断技术有着迫切的需求。数模混合电路中80%以上的故障都来自于模拟电路部分，模拟电路的高故障率和诊断成本一直是困扰电子工业自动化测试的最大瓶颈[1-2]。因此，模拟电路故障诊断一直是一个研究热点，也已经有很多研究成果[3-5]。模拟电路的元器件具有容差特性，且很多故障是元器件性能参数发生变化的软故障，故障样本可辨识性较差，这给故障诊断带来了很大的难度。人工神经网络[6-7]、极限学习机[8-9]和支持向量机[10-11]等是应用较为广泛的分类算法，而SVM具有对样本量需求较小、分类能力强的优点，因此被广泛地用于模拟电路故障诊断。

在SVM的应用过程中，核函数选取和参数设置对其分类效果影响较大，RBF核函数已被证明在非线性问题中有着良好的效果[12]，因此惩罚因子C和核参数gamma的选取成为问题的关键。常见的参数优化方法包括网格搜索算法（GridSearch）、遗传算法（GA）、粒子群算法PSO等。网格搜索算法[13]类似于地毯式搜索，但仅适用于低维数据，且搜索速度较慢；遗传算法[14]是一种有效的全局优化算法，但其收敛速度慢、编码解码过程较为复杂，且其3个算子参数选择主要依靠经验；粒子群优化算法[15]具有易于陷入局部极值点、迭代后期收敛速度慢、准确度较低等缺点。

针对上述问题，本文提出了一种适用于容差模拟电路软故障诊断的正弦余弦算法（SCA）优化支持向量机的分类方法。在对实验电路数据进行小波熵特征提取，采用主元分析法（PCA）进行特征选择后构成故障集，利用SCA-SVM中对故障集进行故障诊断，得到故障分类结果。

1 基于正弦余弦算法的SVM参数优化

1.1 正弦余弦算法

SCA是由Seyedali Mirjalili提出的一种新型类粒子群智能优化算法[16]。在SCA算法中，当正弦函数或余弦函数值的绝对值大于1时，算法进行全局探索；当正弦函数或余弦函数的绝对值介于－1和1之间时，算法进行局部开发，原理如图1所示。SCA算法最显著的特点是借助正弦函数和余弦函数值变化来实现优化搜索，能够探索不同的搜索空间，有效避免陷入局部最优，具有模型简单、调节参数少、收敛速度快、全局寻优能力强等优点。通过SCA算法求解标准测试函数以及与其他多种智能优化算法的比较，均证明了该优化算法的优越性[16-18]。

在正弦余弦算法中，个体位置初始化后采用正弦余弦函数在后续迭代中更新个体位置。具体更新方程为：

式中，为个体X在第t次迭代中的位置，r1、r2、r3为随机数，Pi是当前个体最优解的位置。在计算过程中，有选择地使用上述的位置更新方程：

式中，r4为[0，1]范围中的随机数。

在上述公式中，r1、r2、r3、r4是SCA算法的4个主要参数。其中，参数r1决定了下一次迭代时的位置（或移动方向），它既可以是当前解和目标解之间的区域（图1圆形内部区域），也可以是二者之外的区域（图1圆外侧环形区域）；参数r2为[0，π]之间的随机数，定义了当前移动应该朝向或远离目标解的步进值；参数r3为目标解随机赋予的一个权值，目的是加强（r3＞1）或削弱（r3＜1）所定义的步进值对目标解的影响；参数r4表示如何在式（3）中的正弦和余弦分量之间切换，当r4＜0.5时，按正弦公式进行迭代，当r4≥0.5时，按余弦公式进行迭代。这个设计保证了算法在局部开发和全局探索之间的平衡，正弦和余弦函数的幅值在[－1，1]范围内时是局部开发阶段，在[－2，－1]和[1，2]则是全局探索。

为了平衡局部开发和全局探索，遍历搜索空间内所有区域，并最终收敛得到全局最优解，SCA算法利用式（4）来实现正弦和余弦函数幅值的自适应调节：

式中，t为当前迭代次数，T为最大迭代次数，a为常数。

1.2 SVM支持向量机

SVM是由Cortes等[19]提出的一种建立在VC维和结构风险最小化理论基础之上的机器学习技术，集成了最大间隔超平面、凸二次规划、Mercer核和松弛变量等多种技术理论，尤其适用于小样本、高维度、非线性等工程实际问题，具有很强的泛化能力和机器学习能力[20-21]。

SVM的基本思想是通过映射将低维空间的数据样本转到高维空间中，使它们成为线性可分，再运用线性划分来确定分类边界[22]。对于给定的线性可分样本集：

式中，d为训练样本的维数，n为训练样本的个数，xi为训练样本的输入值，yi为训练样本的输出值。样本被最优分类超平面ω·x＋b＝0完全无误地分为两个类别，且离超平面距离最近的样本与超平面之间的距离最大，离分类超平面最近的两类样本向量称为支持向量。两类支持向量与最优超平面间距之和为，因此，构造最优超平面问题就转化为下述优化问题：

式中，ω为最优超平面法向量，b为偏移量。

对于线性不可分样本，SVM采用非线性映射ϕ将数据样本映射到高维空间进行分类，运用核函数K（xi，yi）解决高维空间维数过高的问题。该核函数满足Mercer条件，其对应于变换空间的内积，即K（xi，yi）＝ϕ（xi）·ϕ（yi），内积运算在未知ϕ（x）具体形式的情况下即可实现[23]，通过选择合适的核函数K（xi，yi）便可实现非线性样本的线性分类。同时，引入一个松弛变量ξ（ξ＞0）将分类面放宽。

引入惩罚因子C以权衡松弛变量ξi的惩罚度，则式（6）转换为：

通过引入Lagrange乘子α将上述约束条件构建的最优超平面问题转化为对偶二次规划问题：

求解式（9），最终得到最优分类决策函数为：

选择不同的核函数将对核函数的分类能力和适用范围产生较大的影响，常用的核函数有线性核函数、多项式核函数、径向基核函数等。本文采用Gauss径向基核函数：

标准SVM是一个二分类算法，在处理模拟电路故障诊断的多分类问题时，需要构造多分类器，可以采用组合若干个二值分类器去构造多类分类器的方法实现[24]。SVM的参数选取对其分类效果有较大的影响，需要确定的参数主要包括惩罚因子C和核参数γ，本文采用SCA算法对其进行寻优。

2 SCA⁃SVM模拟电路故障诊断实验

基于SCA-SVM的模拟电路故障诊断的方法流程如图2所示，主要包括故障注入及数据采集、特征提取、特征选择、SVM参数寻优和故障分类5个主要步骤。

2.1 Sallen-Key带通滤波器电路故障注入及数据提取

实验电路采用Sallen-Key带通滤波器，电路图如图3所示。各元件参数值为元件标称值，元件容差为：电阻±5%，电容±10%。假设当元件参数偏离原值50%即为电路发生软故障，↑表示元件偏大故障，↓表示元件偏小故障。将电路划分为正常状态（non fault-NF）和8种故障状态，分别记为R2↑，R2↓，R3↑，R3↓，C1↑，C1↓，C2↑，C2↓，具体设置如表1所示。

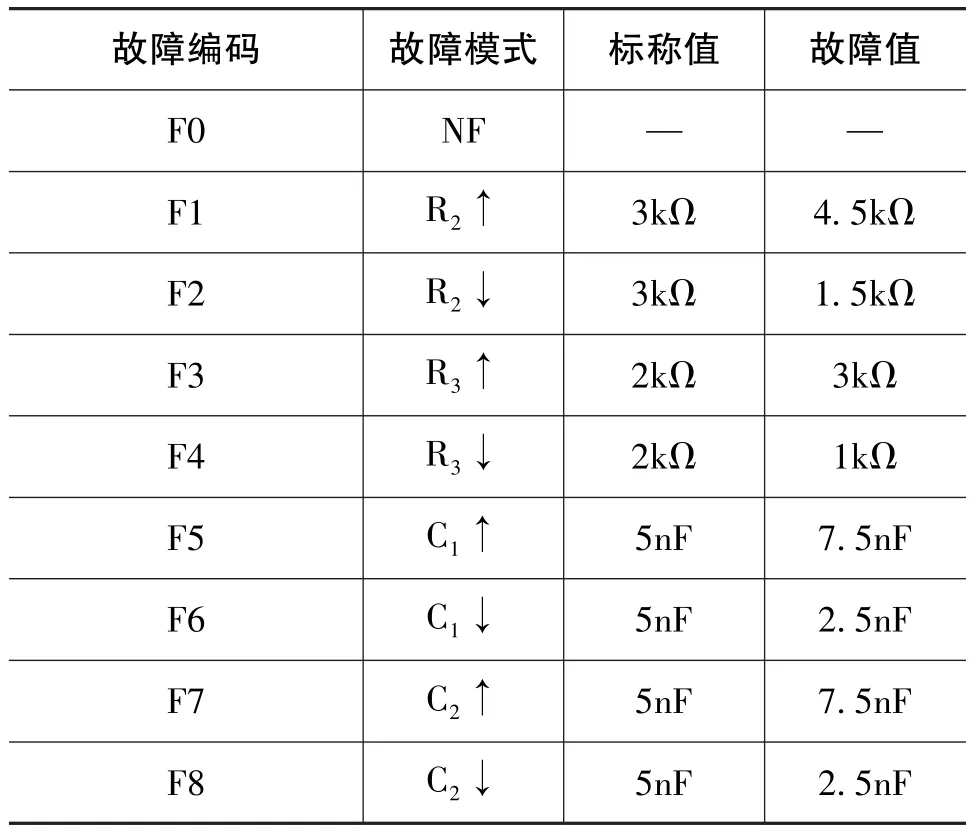
表1 Sallen-Key带通滤波器故障类型及编码Table 1 Fault type and encoding of Sallen-Key band-pass filter circuit

在Cadence16.5中对电路进行仿真实验，所施加激励信号参数如图3所示，对表1所示的故障类别分别进行100次Monte Carlo分析，采集120μs内的输出端波形并保存作为电路输出数据。9种故障共900个样本，从中随机抽取300个样本作为训练集，剩余600个样本作为测试集。

2.2 特征提取与特征选择

对样本集合数据集进行5层小波包变换，得到32个高频和低频序列系数，按照式（12）[25]计算小波包能量熵，构造得到32维特征向量。

式中，Hj，k为小波包能量熵，ej，k（i）为第i个子频带在j层k节点小波包对应能量在总能量中的概率。

32维故障特征向量存在着一些冗余成分会影响故障判别，因此采用主流的主元分析法（PCA）进行特征选择，特征选择阈值选取85%。

2.3 故障诊断及结果分析

经过特征降维后的特征向量即可使用SVM进行分类，本文采用libSVM[26]来实现SVM，使用SCA对SVM的两个参数进行优选。同时，将本文算法与其他算法进行对比，包括网格搜索法（GridSearch）、遗传算法（GA）、粒子群算法（PSO）等。设定相同的libSVM参数c和g搜索范围，c为[0.1，1000]，g为[0.01，1000]，交叉验证参数v均为5。GridSearch步进值为0.1，GA、PSO和SCA均采用相同的迭代次数20和种群规模20，在训练集上的对比结果如表2所示，消耗时间运行环境为四核Intel Core i5-4210U 1.70GHz，4G运行内存。

从表2可以看出，综合分类准确率和消耗时间来看，SCA均表现最优，可见SCA-SVM非常适用于模拟电路故障诊断。使用SCA优选后的SVM参数进行计算，分类结果如图4所示，在测试集上分类准确率达到了99.1667%（595/600）。

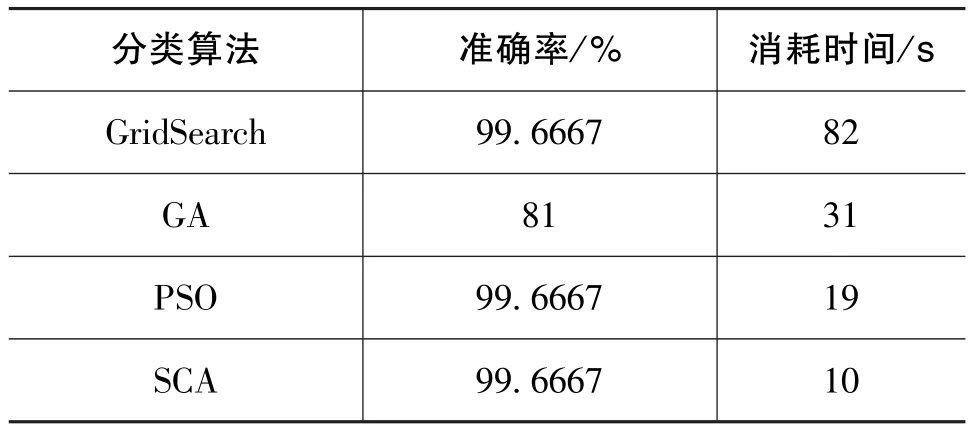
表2 Sallen-Key带通滤波器电路训练集诊断结果Table 2 Diagnosis result of training set on Sallen-Key band-pass filter circuit

3 四运放双二次高通滤波器电路验证

为了验证SCA-SVM分类器的通用性，选择了更复杂的四运放双二次高通滤波器电路作为验证对象，元件标称值和激励信号设置如图5所示，每个故障进行200次Monte Carlo分析。故障类别如表3所示，每个故障抽取前100个样本组成训练集，后100个样本组成测试集。

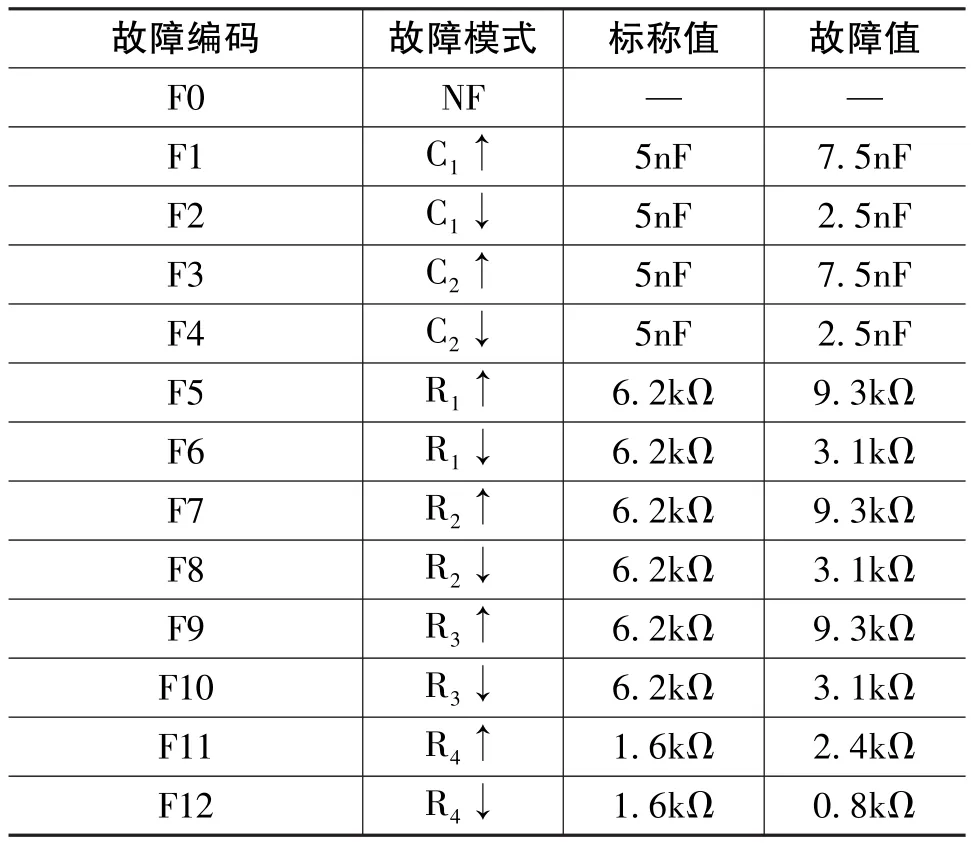
表3 四运放双二次高通滤波器故障类型及编码Table 3 Fault type and encoding of four-opamp biquad highpass filter circuit

继续采用4种不同算法进行验证，算法参数设置同上，4种算法在训练集上的运行情况如表4所示，GA、PSO和SCA三者的详细优化迭代进程如图6所示。

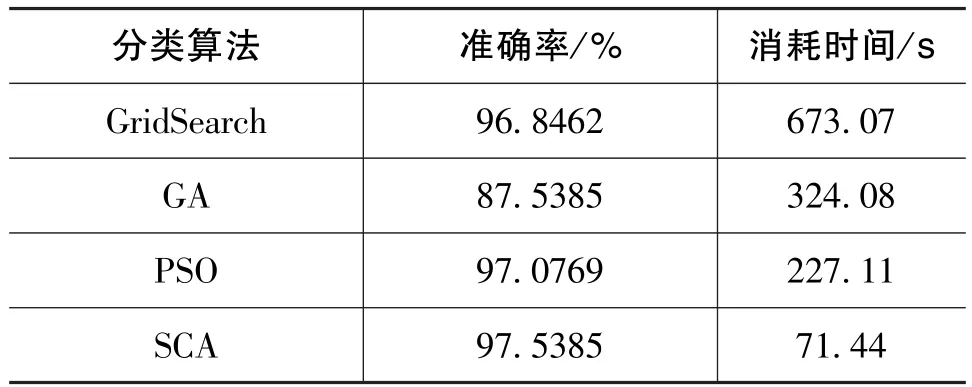
表4 四运放双二次高通滤波器电路训练集诊断结果Table 4 Diagnosis result of training set on four-opamp biquad highpass filter circuit

从表4和图6可以看出，无论是最优分类准确率、运行时间，还是算法的收敛速度，SCA均优于其他3种算法，运行时间远远少于其他算法，算法在第二代即收敛达到最高准确率97.5385%。使用SCA-SVM对测试集进行分类，分类准确率达到了98.38%，算法在测试集上的表现也很好，如图7所示。说明SCA-SVM分类器步进能达到全局最优分类准确率，还具有最快的收敛速度，提高了模拟电路故障诊断的效率。

4 结论

本文提出了一种SCA优化的SVM容差模拟电路软故障诊断方法。

1）SCA-SVM算法可在样本数量较小的情况下得到较高的分类准确率。在Sallen-Key带通滤波器电路实验中，无论是算法迭代速度，还是分类准确率，均优于GridSearch、GA、PSO算法优化的SVM，最后在测试集上的分类准确率也达到了99.1667%。

2）SCA-SVM可以广泛地用于模拟电路故障诊断，使用四运放双二次高通滤波器电路验证算法的通用性，结果显示本文算法仍然在分类准确率和迭代速度上优于其他几种算法。

3）在复杂电路的故障诊断中，虽然分类准确率已经很高，但还是存在一些故障难以区分的情况，这主要是因为它们之间在输出特性上较为相似。因此，可以探索其他更加合适的故障特征提取和特征选择方法来提高此类样本的分类准确率，这也是下一步研究的方向。