面向圆盘造球机动态特性的研究与优化

晏远志，杨金堂，王宏旭，侯作义

（1.武汉科技大学 机械自动化学院，湖北 武汉 430081；2.老河口市绿华环保科技有限公司，湖北 襄阳 441800）

1 引言

圆盘造球机是球团矿生产的重要设备，而其可靠性与稳定性又是影响球团矿质量的关键。在国内，由于圆盘造球机造球质量较好，因而在球团矿生产中应用较多。通过对其使用情况来看，盘体旋转的平稳性还较差，直接影响整机的工作性能，这表明造球系统的动力学性能还有待加强。因此有必要对造球系统结构进行优化以提升其动态特性。

目前国内对圆盘造球机的研究相对较少，设计理论和方法比较单一，常规的运动学分析、静力学分析的方法已不能满足眼前造球机的发展需要。文献[1]分析了圆盘造球机的基本结构，并研究了某些运动学规律；文献[2]对圆盘造球机盘体进行了静力学分析和轻量化设计。目前，还很少有研究人员对圆盘造球机的动态性能作出研究[3]。

以某公司的Φ1800圆盘造球机盘体及传动部分组成的悬臂转子系统为研究对象，利用模态分析、谐响应分析方法对其薄弱部位进行辨识[4]，识别出盘体对该转子系统的动态性能影响最大。以盘体结构作为优化目标，利用尺寸灵敏度分析方法[5]和模糊物元法[6]对盘体进行优化，使其结构更加合理。优化之后的分析结果表明：转子系统的前六阶固有频率都得到了提高，x、y、z三个方向最大共振峰值大幅度降低，悬臂转子系统的动态性能取得较大改善。

2 转子系统动态分析与优化目标确定

2.1 整机模型简化

某公司圆盘造球机，如图1所示。由于造球系统的主要问题是圆盘旋转的平稳性较差，所以仅对由盘体以及支撑轴承、轴承座、传动轴组成的悬臂转子系统进行研究。

图1 圆盘造球机整机结构图Fig．1 Machine Diagram of Disc Pelletizer

在转子系统中，轴承并不是绝对刚性的，会发生弹性变形，因此支承系统就等同于弹簧与转轴串联，对转子系统进行有限元分析的时候，有必要对轴承进行一定的等效。在ANSYS Workbench软件中，采用了Spring单元模拟轴承的支承作用。

2.2 滚动轴承刚度的计算

本结构支承中装有两个滚动轴承，由文献[7]和轴承承受的径向力以及造球机转子系统的结构尺寸，求得滚动轴承的刚度K=6．2×108N/mm。由于在此工况下滚动轴承的阻尼很小，对后面进行动力学分析的影响不大，因此可以忽略[8-9]。

2.3 悬臂转子系统动力学分析

2.3.1 模态分析

利用ANSYS Workbench对悬臂转子系统进行模态分析，得到系统的低阶固有频率与振型情况。设置盘体材料为Q235A（密度为 7850kg/m3，弹性模量为 206GPa，泊松比为 0．3），转轴部件为普通碳钢（密度为7800kg/m3，弹性模量为210GPa，泊松比为0．3）。为了模拟真实工况，保留转轴绕轴线旋转自由度，轴承座与轴承以及轴的结合面采用弹簧单元进行等效，其余接触部分采用绑定接触方式。计算得到转子系统的前六阶固有频率以及前三阶振型情况，分别如表1、图2所示。

表1 悬臂转子系统前六阶固有频率及振型描述Tab.1 First Six Natural Frequencies and Vibration Models of the Rotor System

图2 转子系统前三阶振型图Fig．2 First Three Vibration Models of the Rotor System

由表1与图2可看出，第一阶固有频率近似为0Hz，即刚体模态，可以忽略；转子系统的低阶振型都表现为以盘体结构为主的振动形式，由此可知，盘体就是对转子系统低阶振型影响程度最大的结构件。

2.3.2 谐响应分析

为了反映转子系统在矿球激励下的动态性能变化情况，以盘底为参考点，在盘体底面和内壁分别施加幅值为1000N和250N，频率为（0～60）Hz的简谐力，测得转子系统位移频响曲线图，如图3所示。

图3 转子系统在x、y、z三个方向的谐响应曲线Fig．3 Harmonic Response Curve of x、y、z in Three Directions of the Rotor System

从图3可看出，转子系统在x、y、z三个方向上的最大共振峰值均出现在28Hz，这对应于系统的第四阶固有频率。在y、z方向上，系统在17Hz即第二固有阶频率也出现了共振峰值。由于共振峰值最大的频率点即为转子系统的最薄弱共振点，因此系统的第四阶固有频率即对其动态性能影响最大。

2.4 转子系统优化目标的确定

由以上分析表明，盘体结构对转子系统的低阶振型影响最大；而系统的第四阶固有频率在三个方向上对系统的动态性能影响最大。由于转子系统结构的每阶固有频率对应一个振型，所以可判断盘体结构为影响转子系统动态性能的关键部位。通过对盘体结构进行优化设计，可避免对转子系统动态性能优化的盲目性，提高优化效率。

3 盘体结构的优化设计

由于盘体结构尺寸较为复杂，各尺寸参数对盘体结构模态的贡献不同，而且在结构设计中，为提高结构的固有频率往往会增加板的厚度，这虽然会增加了刚度，但同时也增加其质量，因此先采用灵敏度分析的方法确定各尺寸参数对盘体结构的第四阶固有频率和质量的影响程度，然后对比较敏感的参数进行优化设计。

3.1 灵敏度分析

利用ANSYS Workbench中的Design Exploration下的Response Surface Optimization进行灵敏度分析，盘体的各个尺寸参数在盘体中的具体位置，如图4所示。

图4 盘体尺寸位置简图Fig．4 Position Sketch of Disk Body Size

各待优化参数对应的参数符号、初值以及范围，如表2所示。计算出这些分析尺寸对转子系统的第四阶固有频率和质量的灵敏度大小，如图5所示。

表2 选定尺寸的变化范围Tab.2 Selected Size Range

图5 各优化变量对第四阶固有频率和质量的灵敏度Fig.5 Sensitivity about Fourth Natural Frequency and Quality of Each Optimization Variables

由图5可知，与第四阶固有频率成反比的尺寸是：P4，P3；成正比的是：P6、P1、P5且P2、P7对第四阶固有频率几乎无影响。对盘体质量的影响大小顺序是：P3、P4、P1、P6 且 P2、P5、P7 对质量几乎无影响。

综合本次灵敏度分析的结果，剔除对第四阶固有频率和质量影响较小的参数，选择P1、P3、P4、P6作为设计变量，对盘体结构进行优化。

3.2 盘体结构优化分析

根据上文分析结果，将盘体结构的第四阶固有频率和质量作为优化目标，将盘体的尺寸参数 P1、P6、P3、P4 依次设为 x1，x2，x3，x4作为优化参数。在ANSYS Workbench中的Response Surface Optimization下的Optimization优化分析模块中经过反复优化迭代求解后得到5组候选设计点，原设计方案与优化之后的候选设计点，如表3所示。

表3 优化设计结果Tab.3 Optimization Design Results

3.3 最优设计方案

盘体模态评价是一个多指标决策过程，存在单项指标评价结果的不相容性问题，因此需要借助评价方法获取最优的设计方案。利用基于熵权的模糊物元分析法作为评价模型[10]，获得造球机盘体的最优设计方案，其步骤如下。

3.3.1 确定模糊物元判断矩阵R

盘体模态优化中事物M有C1，C2，…，C66个特征及其相应的量值，这些构成了5种事物的6维复合模糊物元判断矩阵R。

式中：Ci（i=1，…6）—特征评价指标；Mj（j=1，…，5）—各设计方案。

3.3.2 确定从优隶属度矩阵

由于每个评价指标的特征值对于设计方案来讲，有的成正比，有的成反比，所以对不一样的从优隶属度uij分别要利用不同的公式进行求解。

若评价指标Ci的值与频率f成正比时，则使用效益型指标：

若评价指标Ci的值与频率f成反比时，则使用成本型指标：

式中：xij—矩阵R中方案Mj的指标Ci所对应的属性值。在6种指标中x1，x2和f对模态频率来说越大越好，故选用效益型指标，其余选用成本型指标。利用上式对模糊物元判断矩阵进行计算得到从优隶属度uij。其中uij为从优隶属度矩阵R~nm中对应的元素，从而得到矩阵R~nm。

3.3.3 计算评价指标的熵和权重

由于评价指标权重反映的是各指标对评估方案的影响程度，所以确定指标权重对于准确地进行评估十分的重要。则利用熵权法计算评价指标的权重。由隶属度矩阵中n个评价指标和m个评价对象得到第i个评价指标的熵为：

计算得到评价指标的熵向量 H=（0.982，0.981，0.982，0.985，0.980）T，最后得到第i个指标的权重为：

计算得到评估指标权重向量 K=（0.1999，0.2164，0.1947，0.1625，0.2263）。盘体各优化方案的优劣由下式确定：

通过计算得到优劣性能向量 P=（0.2203，0.5966，0.3052，0.6958，0.8375），由向量P可知，盘体的优化设计方案优劣依次为：M5，M4，M2，M3，M1；因此 M5为最优设计方案。由设计方案 M5表明：该方案中转子系统相对于原来第四阶固有频率增加了24.48%，盘体质量减小了15.55%。

4 优化结果验证

在选择方案M5，且相同的边界条件下，经验证转子系统满足静刚度要求，盘体优化前后转子系统的前六阶固有频率对比结果，如表4所示。

表4 盘体优化前后转子系统前六阶固有频率（Hz）Tab.4 First Six Natural Frequencies of Rotor System before and after Disk Body Optimize

表4表明，优化后的悬臂转子系统前六固有阶频率均得到了不同程度的提高。优化前后转子系统在x、y、z方向上的位移频响曲线，如图6所示。

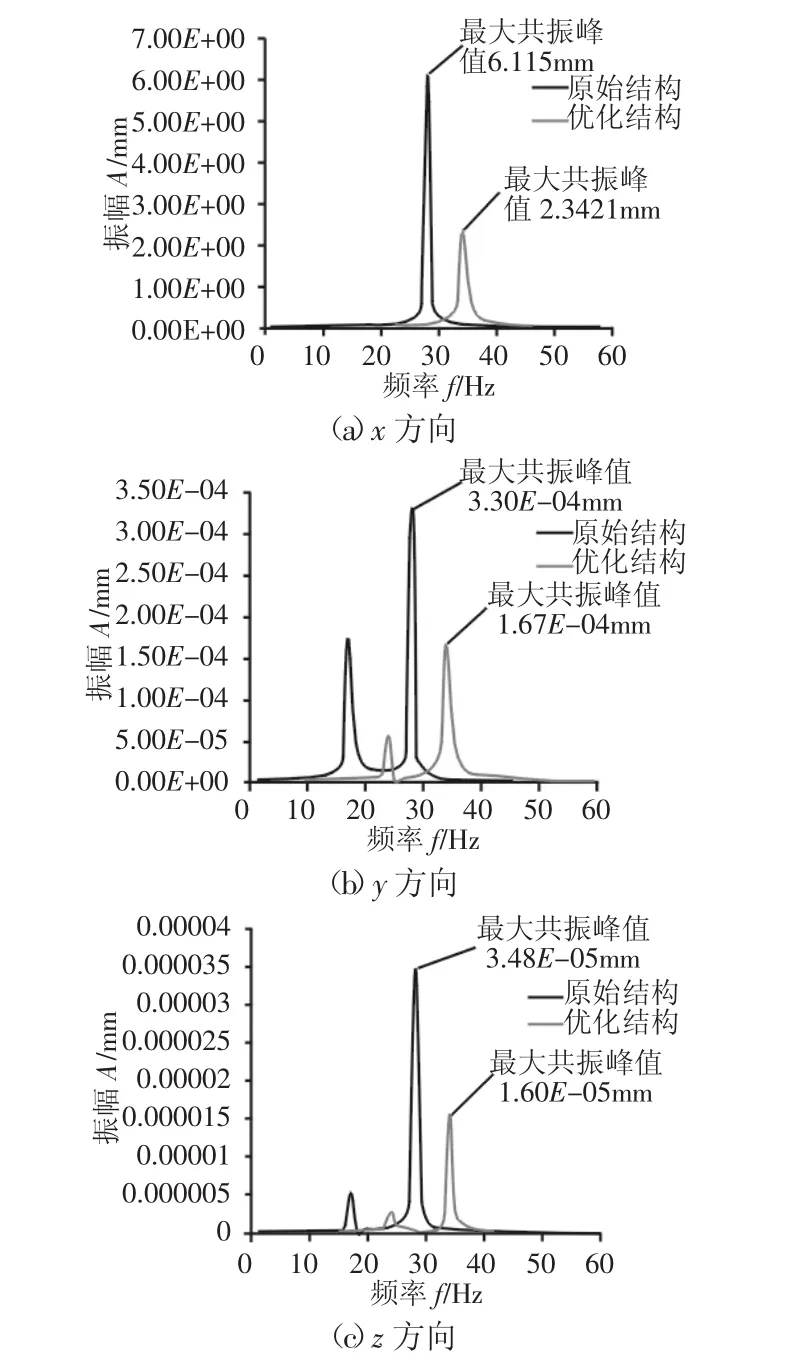
图6 转子系统优化前后三个方向谐响应分析对比Fig.6 Comparison of Harmonic Response in Three Directions of Rotors System before and after Optimize

由表4和图6分析可知，在三个方向上，转子系统的最大共振频率均由原始结构的28.097Hz提高到34.976 Hz；并且在x方向对应的最大共振峰值下降了61.7%，在y方向上下降了49.4%，z方向下降了54.0%。以上分析结果表明：转子系统结构在三个方向上的最大共振峰值均得到了大幅度地降低，这说明其抵抗外界动态干扰的能力得到了较大的提高。

综上所述，在减轻盘体质量与保证转子系统静刚度的前提下，优化后的盘体结构能够改善转子系统的动态性能。

5 结论

（1）通过对圆盘造球机悬臂转子系统的模态分析，得出盘体是对转子系统低阶振型影响程度最大的结构件，由谐响应分析表明转子系统x、y、z方向上的最大振幅值分别为：6.115mm，3.30×10-4mm，3.48×10-5mm均出现在28Hz即系统的第四阶固有频率，由此可以确定盘体是转子系统动态性能的薄弱环节。

（2）确定盘体结构是优化目标后，采用灵敏度分析的方法计算盘体分析尺寸对其结构的模态和质量的影响程度，确定优化尺寸参数，避免了对盘体优化的盲目性。

（3）通过ANSYS Workbench优化分析得到5组候选设计点，在此基础上通过基于熵权的模糊物元法获取最优设计方案。优化设计结果表明，与原始结构相比，转子系统在x、y、z三个方向上的最大振幅分别下降约60.5%、49.4%、54.0%。