基于三角模糊多属性决策的卫生应急能力组合评价模型设计与比较*

潍坊医学院“健康山东”重大社会风险预测与治理协同创新中心(261053)　

李望晨　王素珍　郑文贵　王春平△　张利平△

【提　要】　目的　基于三角模糊数测度和多种决策方法设计组合建模方案,以卫生应急能力综合评价为例,经流程演示和案例验证比较,为类似问题应用者提供借鉴。方法　以模糊评语资料为基础,将三角模糊数与TOPSIS、灰色关联、投影寻踪、VIKOR及相对贴近度思想结合设计多种模型,再折中设计组合模型并比较相关性。结果　理论程序明确、实施步骤具体、测量信息利用充分。相关结果有统计意义。结论　组合模型将结果一致性折中,相比单项方法更有指导意义,为卫生评价或决策问题研究提供方法参考。

多属性决策(多指标评价)是在多属性(指标)测度信息基础上,经属性(指标)筛选、权重计算、测评及预处理、将备选方案(待评对象)在群体间相对比较、择优或排序[1]。鉴于经验认知有限性、判断思维模糊性、环境复杂多变性,测量信息不再适于精确数描述,区间数、模糊数更适合于描述这类问题。不确定或模糊决策方法在应用领域较滞后,评价工作常以精确数测度为基础、套用传统简单方法为主,在模糊或不确定性指标测度时,须对模糊处理技术及不确定决策方法给予关注。由于决策(评价)问题中可选方法的多样性,也造成了决策(评价)结果不唯一性或非一致性,但是方法提出往往均有存在合理性,难以确定以哪种结果指导实践更科学,须结合算法原理来解读才更有效意义。因此,有必要从多种方法结果一致性出发,将多种方法结果折中处理和设计组合模型。以方法论改进为背景,基于三角模糊数知识的指标测度信息为基础,引入TOPSIS[2]、灰色关联[3]、投影寻踪[4]、VIKOR[5]和相对贴近度观点,设计综合评价模型组合建模途径。最后,以卫生应急能力评价算例验证分析,为卫生决策类似问题提供技术借鉴。

模糊测度

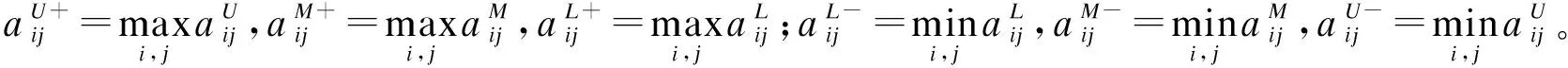
建模方案

1.三角模糊TOPSIS法

群体中可以虚拟构建正、负理想对象,计算每个对象与之的距离、相对距离。

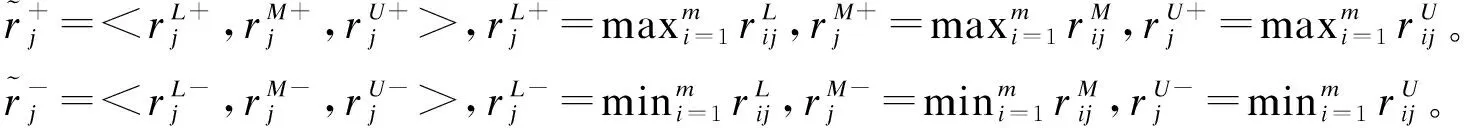
(1)

(2)

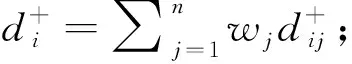
(3)

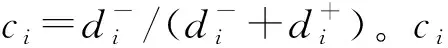
(4)

2.三角模糊灰色关联法

群体中可以构建正、负理想对象,计算每个对象与之关联度、相对贴近度。

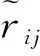
(5)

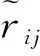
(6)

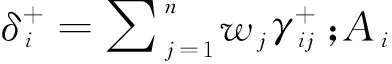
(7)

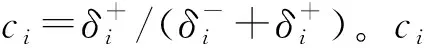
(8)

3.三角模糊投影寻踪法

群体中可以构建正、负理想对象,计算每个对象与之加权投影、相对贴近度。

假设α=(a1,a2,…,an),β=(b1,b2,…,bn)为两个向量,则α在β上投影:

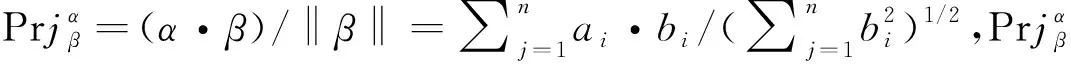
定义三角模糊数内积运算:

由此分别将Ai向理想对象A+、负理想对象A-向Ai计算加权投影:

(9)

(10)

(11)

4.三角模糊VIKOR法

不妨以“最大化群体效用、最小化个体遗憾”原则逼近理想解,再作折中排序。

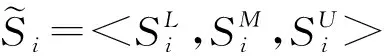
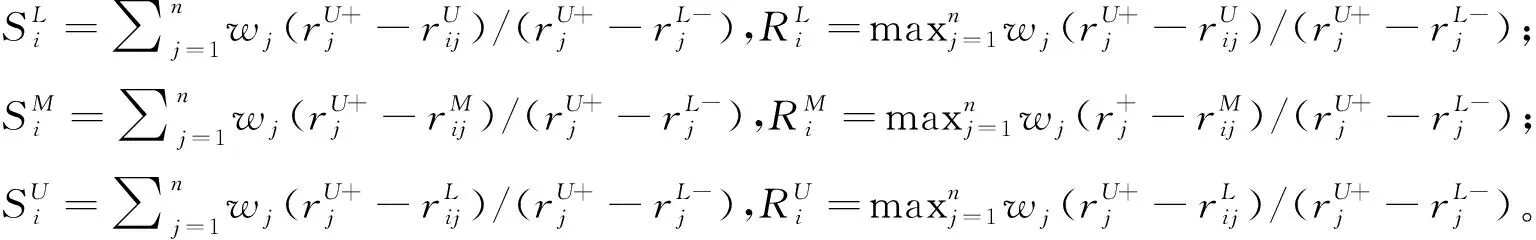
(12)

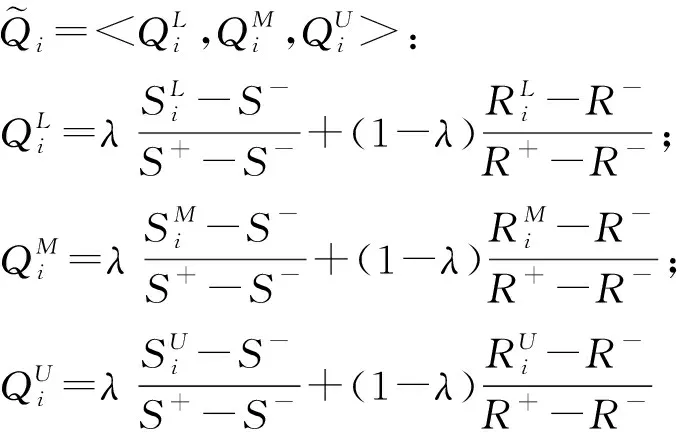
(13)

(14)

(15)

vi越小则方案Ai相对越优;vi越大则方案Ai相对越劣。

5.组合设计

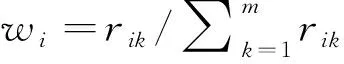
案例实证

1.对象资料

以疾控机构卫生应急能力测评为例验证可行性、比较差异性,从预案、队伍、储备、监测、预警、报告维度细化指标[6-7]:c1预案完备性、c2预案可操作性、c3预案维护与修订、c4预案培训与演练、c5组织机构建设、c6专业构成与技术水平、c7培训演练计划方案、c8培训实施与资料归档、c9法规政策保障、c10资源储备、c11储备物资评估管理、c12危险源重点防护监管、c13预测预报评价、c14信息收集分析、c15预警体系建设、c16报告上报时间、c17报告完整性和c18报告准确性。

指标c1～c18权重分别对应为w1～w18[6]:0.056,0.0587,0.0507,0.0587,0.0613,0.0587,0.0587,0.048,0.056,0.056,0.0533,0.0533,0.048,0.0587,0.0507,0.0613,0.0587,0.0533。

以模糊评语(语言变量)形式表达指标优劣,将其转化三角模糊数测度[8],关系如下:“很差=I”<0,1,3>、“差=II”<1,3,5>、“一般=III”<3,5,7>、“好=IV”<5,7,9>、“很好=V”<7,9,10>。专家组以调查、访谈、研判和会商方式,对7所县级机构A1～A7所有指标研制评语,因篇幅和侧重点不再赘述过程,见表1。

表1　专家对机构A1～A7指标评语

表1中评语全部转化为三角模糊数,由于指标全部为正向且为同类型,不妨预处理:“I”<0,0.1,0.3>、“II”<0.1,0.3,0.5>、“III”<0.3,0.5,0.7>、“IV”<0.5,0.7,0.9>、“V”<0.7,0.9,1>，仅以机构A1为例:

A1=(<0.3,0.5,0.7>,<0.3,0.5,0.7>,<0.3,0.5,0.7>,<0.7,0.9,1>,<0.7,0.9,1>,<0.3,0.5,0.7>,<0.3,0.5,0.7>,<0.3,0.5,0.7>,<0.1,0.3,0.5>,<0.5,0.7,0.9>,<0.7,0.9,1>,<0.7,0.9,1>,<0.3,0.5,0.7>,<0.5,0.7,0.9>,<0.3,0.5,0.7>,<0.5,0.7,0.9>,<0.3,0.5,0.7>,<0.7,0.9,1>)。机构A2～A7类似A1,可由表1资料逐个列出,此处省略。

2.三角模糊TOPSIS法

按指标取最优、最劣值,虚构正理想和负理想疾控机构A+、A-:

A+=(很好,很好,好,很好,很好,很好,好,好,好,好,很好,很好,好,很好,很好,好,很好,很好);

A+=(V,V,IV,V,V,V,IV,IV,IV,IV,V,V,IV,V,V,IV,V,V);

A+=(<0.7,0.9,1>,<0.7,0.9,1>,<0.5,0.7,0.9>,<0.7,0.9,1>,<0.7,0.9,1>,<0.7,0.9,1>,<0.5,0.7,0.9>,<0.5,0.7,0.9>,<0.5,0.7,0.9>,<0.5,0.7,0.9>,<0.7,0.9,1>,<0.7,0.9,1>,<0.5,0.7,0.9>,<0.7,0.9,1>,<0.7,0.9,1>,<0.5,0.7,0.9>,<0.7,0.9,1>,<0.7,0.9,1>)。

A-=(差,一般,差,一般,差,一般,一般,一般,差,一般,一般,一般,差,一般,一般,差,一般,一般);

A-=(II,III,II,III,II,III,III,III,II,III,III,III,II,III,III,II,III,III);

A-=(<0.1,0.3,0.5>,<0.3,0.5,0.7>,<0.1,0.3,0.5>,<0.3,0.5,0.7>,<0.1,0.3,0.5>,<0.3,0.5,0.7>,<0.3,0.5,0.7>,<0.3,0.5,0.7>,<0.1,0.3,0.5>,<0.3,0.5,0.7>,<0.3,0.5,0.7>,<0.3,0.5,0.7>,<0.1,0.3,0.5>,<0.3,0.5,0.7>,<0.3,0.5,0.7>,<0.1,0.3,0.5>,<0.3,0.5,0.7>,<0.3,0.5,0.7>)。

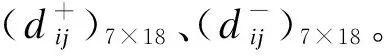
由公式(3)计算A1～A7与A+、A-之间距离:

由公式(4)计算Ai与A-相对距离ci:0.499,0.456,0.391,0.384,0.665,0.676,0.505。

由ci对A1～A7相对排序A6≻A5≻A1≻A7≻A2≻A3≻A4。

3.三角模糊灰色关联法

由公式(7)计算A1～A7与A+、A-灰色关联度:

由公式(8)计算Ai与A-相对贴近度ci:0.496,0.483,0.446,0.461,0.575,0.562,0.496。

由ci对A1～A7相对排序:A5≻A6≻A1≻A7≻A2≻A4≻A3。

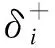
同理,若ρ=0.2则由公式(5)～(8)计算ci:0.494,0.473,0.407,0.437,0.638,0.597,0.487。

由ci对A1～A7相对排序:A6≻A5≻A1≻A7≻A2≻A4≻A3。

若ρ=0.8则由公式(5)～(8)计算ci:0.504,0.494,0.469,0.477,0.558,0.552,0.505。

由ci对A1～A7相对排序:A5≻A6≻A7≻A1≻A2≻A4≻A3。

4.三角模糊投影寻踪法

由公式(9)、(10)将A1～A7向A+,以及将A-向A1～A7上计算加权投影:

由公式(11)计算Ai与A-相对贴近度ci:0.541,0.536,0.534,0.526,0.551,0.555,0.540。

标记投影寻踪(相对贴近)法,由ci对A1～A7相对排序A6≻A5≻A1≻A7≻A2≻A3≻A4。

5.三角模糊VIKOR法

令λ=0.5,由公式(14)依次两两计算pij,将其全部列入矩阵(pij)7×7:

p23=0.5×max{1-max((0.619-0.161)/(0.619-0.238+0.488-0.161),0),0}+0.5×max{1-max(0.997-0.488)/(0.829-0.488+0.997-0.619),0),0}=0.341。

由公式(15)计算A1～A7排序数v1～v7:0.135,0.143,0.171,0.170,0.121,0.121,0.137。

其中v2=(0.538+0.500+0.341+0.342+0.614+0.630+0.537)+7/2-1)/(7×6)=0.143。

由vi对A1～A7相对排序:A6≻A5≻A1≻A7≻A2≻A4≻A3。

若λ=0.2,同理计算排序数v1～v7:0.134,0.137,0.171,0.173,0.128,0.125,0.132。

由vi对A1～A7相对排序:A6≻A5≻A7≻A1≻A2≻A3≻A4。

若λ=0.8,同理计算排序数v1～v7:0.139,0.148,0.167,0.164,0.121,0.119,0.142。

由vi对A1～A7相对排序:A6≻A5≻A1≻A7≻A2≻A4≻A3。

6.组合分析

每种方法结果汇总,比较A1～A7优劣次序,从结果分析(表2)认为A5、A6较好,A6更好;A3、A4较差,A3更差。各方法结果的等级相关性有统计学意义(P=0.003～0.000)。

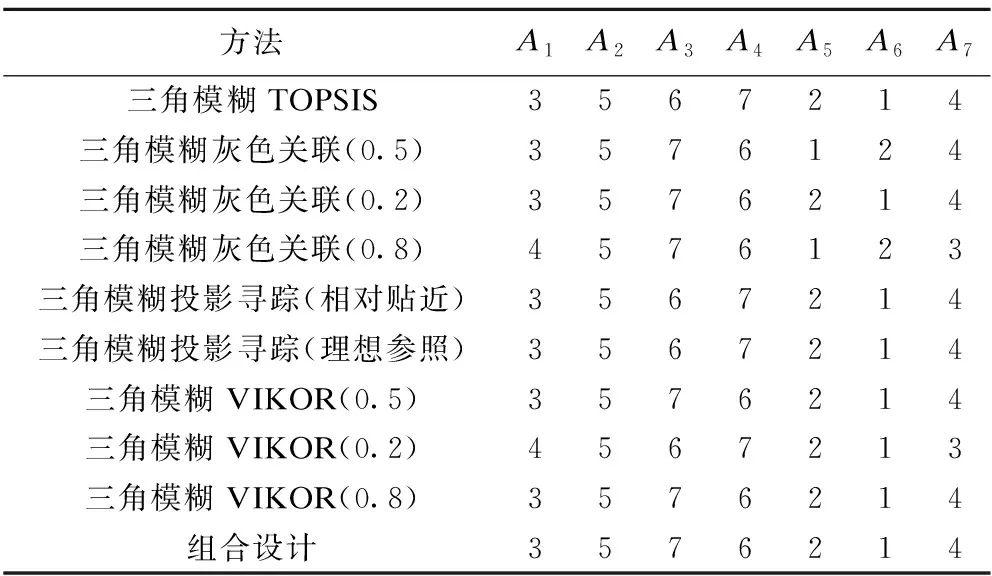
表2　各种方法对机构A1～A7排出优劣次序

将每种方法与其他方法的相关系数相加,归一化计算每种方法的权重,0.1004,0.1332,0.1010,0.1301,0.1004,0.1004,0.1010,0.1326,0.1010。权重越大则该方法与其他方法结果越相似。从多种结果一致性来建立多种方法组合模型,将评价结果与权重合成最终结果3.263,5.000,6.566,6.434,1.737,1.263,3.737,优劣次序为3,5,7,6,2,1,4,A6≻A5≻A1≻A7≻A2≻A4≻A3,于是可认为A6最好、A4最差。

讨　　论

传统综合评价问题多见且为辅助卫生管理工作而提出,应用研究常以指标量表打分和客观数据资料计算为基础,以往经典方法简单却缺乏新颖性,测评资料收集方式和表现特点也限制了模型设计思路的扩展与改进。模糊多属性决策为主观测度资料情境下的建模方案提供了新途径,但是在卫生工作应用中探索引进比较滞后且未受关注。例如,由于经验有限性、认识模糊性、环境不定性,如应急能力、医患满意等主观性指标测度时难以精确数描述,更适于模糊评语(语言变量)测度下组织专家主观研判。传统方法背景下已经无法利用此类信息,模糊决策技术引入对于此类决策工作是必要的。

本文以三角模糊数测度为基础论证多属性决策模型设计流程。首先简述三角模糊数表示、属性值预处理知识。然后以语言变量转化后的三角模糊数为测度基础,以交叉学科理论为基础,将模糊信息技术与TOPSIS、灰色关联、投影寻踪、VIKOR法以及相对贴近度思想等综合评价方法结合设计模型,又通过组合模型将多种方法结果的不一致性进行折中与修正,从整体相关性视角将其加权合成组合结果。最后以卫生应急能力评价为例验证可行有效性,从而在卫生决策问题中扩展推介这些方案适用性,逐项应急能力指标等级评语信息转化为三角模糊数形式,由多种方法分别建模实现流程,从组合设计角度寻求折中结果,分析信息利用特点并凸显比较了性能。组合模型将多属性决策多种方法将近似结果继续折中,更适于此类评价或决策工作的测评信息表述与认知规律提取。