一个“米”字破解“诱导公式”——观连春兴老师授课有感

温长远

(上海市华东师范大学第二附属中学　211203)

1　缘起

笔者目前所在校是一所新建校，由于工作需要，我们聘请连春兴老师作为数学学科辅导教师.根据学校实际，连老师给我们传递了很多好的理念，如，把学生的“广泛参与、深入思考”作为评估一节好课的核心标准；课堂教学应该以问题驱动，尽力让学生在相对独立地解决问题的过程中，发现新知、获取新知.这些理念聚焦于学生的学科素养，符合现代教育观，但如何在教学中实施？尤其针对我们新建校中等偏下的生源基础，能否找到切实可行的实践途径？带着这些疑虑，我们诚邀连老师为我们学生上一节示范课.当了解到我们初、高中的进度后，连老师欣然应允，选了一节既能体现他的理念，又无需刻意准备，即使不用信息技术辅助，也无大碍的“诱导公式”课.出乎意料的是，连老师用一个“米”字破解了“诱导公式”，让人大开眼界.

2　授课简介

也许是考虑到学生基础，上课伊始，连老师徒手画了一个以原点为心的单位圆，以及角α的终边与圆周交于点P(x,y)，采用学生回答的方式复习了三角函数的定义，然后进入问题驱动环节.

问题1如果角α=30°，请同学们写出一些正弦值与sin30°相同或为相反数的角.

照理说，在定义的启发下，回答这个问题并不困难，但学生的回答耐人寻味.先是一位同学回答390°，750°， 1110°，再是一位同学补充回答-330°，-690°，-1050°，这些角的终边都与30°相同，显然不是连老师所希望的，但他没有丝毫的埋怨，笑容可掬地肯定了大家对“整圈白转”诱导公式理解到位，然后耐心启发大家，除了整圈，还有没有非整圈情况，在一整圈的旋转过程中，还有其它角满足条件吗？正是“千呼万唤始出来”，学生终于七嘴八舌补齐了“-30°， 150°，210°”.

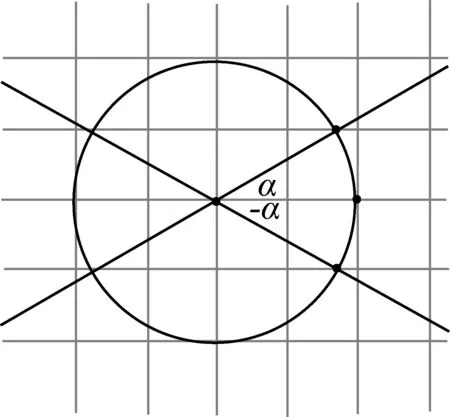
问题2如果角α是任意锐角，请同学们画出与sinα相同或为相反数的角的终边.

在前面“30°，-30°， 150°，210°”终边位置的启发下，学生很自然的画出终边关于x轴、y轴、原点对称的三种情况，一个“米”字，初见端倪.

问题3请大家把问题2中终边相对应的角用最简捷形式表示出来，并观察该图，写出观察到的等式.

问题4把正弦变成余弦和正切又如何？

这两个问题是本节内容的核心，能否由学生在观察中解决，事关“学生在解决问题过程中，发现新知、获取新知”理念的实施，而后学生的表现说明我们这种担心是多余的，在“米字”的情境中，学生完全可以独立发现“诱导公式”.三位同学在黑板上展示自己的观察结果如下：

(学生口述，教师代笔).

从先后三位同学朴实无华、顺序不一的回答看，他们不可能有任何前期的预习与准备，纯属自然生成，可谓本课精彩的一笔.得到正弦、余弦、正切三组公式后，连老师靠追问方式提炼了公式的记忆方法，尤其是符号规律，然后话锋一转，提出为了使这些公式获得更广泛的运用空间，我们一起来研究α非锐角时，公式是否成立.

问题5当α为任意角时，这些公式是否成立？

这是一个在数学基础不太好的同学眼里，无所措手足的问题，如果放手让学生探究，课堂效率难以保证，所以连老师采用择一示范性讲解，其余由学生课后探究的方式处理.

如图，角α为第二象限角，先画出-α的终边，再画出-α+π=π-α的终边，结果学生易见角α与π-α的终边仍然关于y轴对称，遂得sin(π-α)=sinα成立.当角α为三、四象限角或轴上角时，自行证明.其余公式仿此处理.

问题6请完成如下求值：

(1)sin870°；(2)cos(-225°)；

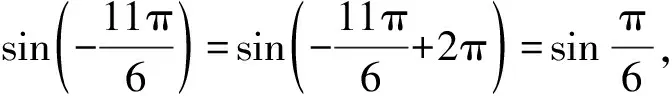
最后总结诱导公式的使用，一般情况采用“负化正，去(或加)整圈，去半圈”的策略(下课).

3　课后反思

一节普通的数学课，却被连老师上得如此精彩，听完后大家的心情久久不能平静，越回味越感到似陈坛老酒，醇香厚重，韵味绵长，给我们留下了诸多有益的启示.

3.1　关于知识的理解

过去我们讲授诱导公式，大多只把它作为三角函数求值，化简的工具，而且教学中按照课本的顺序呈现，这样就导致了公式的产生不够自然，公式之间缺乏内在联系，即使教师生硬的引导学生观察对称性，也仅仅是生硬的获得公式，虽然这样学生也可以被动地接受，但后续的公式运用与记忆，都或多或少的存在问题，基础薄弱的学生尤甚.面对这样的现状，有的教师直到现在，还固守“奇变偶不变，符号看象限”的陈词滥调，引导学生机械地记忆与使用.殊不知，诱导公式不仅是三角函数求值，化简的工具，还是三角函数的重要性质，之所以在角的终边绕原点旋转的过程中，函数值会不断出现相等或相反(数)的变化，究其根源，不难发现，这是作为刻画圆周运动的三角函数,其周期性和对称性所决定的.连老师正是抓住了三角函数这个重要特征，引导学生成功地构造了一个“米”字，成功破解了诱导公式的密码，使诱导公式变成了不记而记的事实.

3.2　关于导学的问题

连老师这节课为什么成功？其根本原因在于他导学问题的设定.试想，若按连老师以学生“广泛参与、深入思考”作为评估一节好课的核心标准，这就自然提出一个问题：学生怎样参与？参与什么？平台在哪？谁来搭建？这种种疑惑，这节课给出了明确的回答，那就是教师搭建便于学生参与的问题平台，其中起决定作用的是初始问题的设置.

若按照教材(人教A版数学4)的提供的探究任务，给出一个任意角α，研究π±α的终边与之的对称关系，也得到诱导公式，而且还省去了诱导公式对α是任意角时是否成立的讨论，但这样做，与连老师的初始问题比，起点无疑是高的，而且α原本是任意角，却按α是锐角时记忆符号，这个中原委，至少在学生看来，也不够清晰.连老师充分考虑了学情，从问题1“写出一些正弦值与sin30°相同或为相反数的角”出发，扩充到问题2“任意锐角”，发现函数值相等或相反(数)的角的终边，是万变不离其宗——一个“米”字.就是这样一个从“任意角”到“锐角”降低门槛的变化，无疑给学生搭建了有利于“广泛参与，深入思考”的平台，随后在α是锐角的基础上，符号记忆规律变得无需解释，而问题5“对α是任意角时，诱导公式是否成立的讨论”，又使逻辑上无懈可击.这样在知识的制高点不变的前提下“削山填路”的做法，特别在我们基础薄弱的学校是值得提倡的.

连老师多次在讲座中提到，导学的问题务必要遵循如下原则：

(1)起点问题要尊重学生的认知基础，激发兴趣，开门见山，直击知识主题.

(2)问题延伸要先具体，后抽象，先特殊，后一般，给学生观察发现、归纳总结的机会.

(3)系列问题要体现知识发生、发展的逻辑走向，且符合量力性原则.

(4)问题设置要照顾到不同层次的学生，最好有一定的开放性.

如果连老师不给我们真实的上一节课，我们对这些导学原则的理解往往是苍白的.而通过连老师这节课的诠释，我们不难发现，他本人严格遵循了这些原则.抛开尊重学生认知基础，且直击知识主题的问题1不说，从问题1，2，3，4，5的延伸来看，它们既符合从具体到抽象，从特殊到一般、便于学生参与的呈现要求，又在遵循量力性原则基础上，揭示了知识发生、发展的逻辑走向，特别是问题5，既是逻辑的完善，也同时为能力较强的学生自主学习，提供了一个相对开放的空间.这样一些可以由学习者拾级而上、渐次解决的系列问题，无疑在学生学习过程中，可以发挥路标与拐杖的功能，使“尽力让学生在相对独立地解决问题过程中，发现新知、获取新知”成为可能.

3.3　关于教学的艺术

教学是一门艺术，这种艺术既体现在宏观设计上，也体现在微观处理上.如果说，前文提到导学问题是在宏观设计上的艺术体现，那么在微观处理上看，连老师的教学也有许多可圈可点之处.

首先是恰如其分地引导和机智幽默地师生对话.如解决问题3时的那位同学写出包括“sinα=sinα”在内的四个公式后，连老师在充分肯定的基础上，调侃“sinα=sinα”是正确的废话，引发同学的哄堂大笑；解决问题4时那位同学写出关于余弦的三个公式后，连老师追问：这个地方凭什么取负？引发同学们对符号的警醒；当汇报正切三个公式的同学把最简单的“tan(-α)=-tanα” 写在第一位置时，连老师夸赞他“先吃软柿子”，又一次引发学生会心的微笑；当学生完成了三个公式的总结后，连老师又不无警惕的向大家发问：(对照黑板)你们凭什么不出错？请大家判断可能在哪里出错？以发问的方式，再次引发同学对符号的重视，收到画龙点睛之效；随后连老师又鼓动大家为生成知识做出贡献的同学表示祝贺时，顿时响起热烈的掌声；在诱导公式的运用阶段，他充满关爱的对学生说：“你能独立完成更好，遇到困难不能独立完成时，再看黑板(正确的板演)”；“我错怪你了，有可能你说‘正’是因为两个负号抵消的结果”；“这个公式的选择是很智慧的，我祝贺你们！”这毫无做作的教学语言，是连老师对学生大爱的自然流露，如此风格的师生交流，拉近了原本陌生的师生距离，营造了轻松愉悦的课堂氛围.

其次是连老师非常关注课堂上学情的反馈.也许与他面对陌生的学生群体有关，他一节课不下5次要求“与黑板上结论一致的同学请举手”，以统计学生掌握的真实情况，避免被少数优秀学生的表现所误导，并根据学生准确率情况，从容把握着课堂节奏.尤其是学生举手附议较少时，依然可见连老师不急不躁、语速舒缓、微笑着的期待眼神.

再次是细节处理的细腻.如当学生完成关于正弦、余弦、正切的三组诱导公式后，及时提醒大家看书，指出同学们的总结，与教材诱导公式(2)，(3)，(4)的区别在于按同名函数分类和按角的关系分类，以排除学生可能存在的阅读困难.再如，连老师总是先用自然语言给同学布置任务，等大家进入思考状后，再以问题的形式在黑板上板书，这样一方面有助于学生准确地领会任务，也避免了不用信息技术展示，因书写速度不及阅读速度引发的时间耽误.

最后一点最重要，那就是“当讲则讲”.华东师大的张奠宙先生曾针对一味强调学生自主探究，影响课堂效率的现象告诫我们，中国的数学教学，万不可削弱教师的示范性讲解.连老师的教学处

理暗合了这种提法，如本课问题5的解决，他并没有给学生多少思考的时间，而是当仁不让，选择讲解α是第二象限角时，角α与π-α终边仍然关于y轴对称，于是公式sin(π-α)=sinα成立.再如问题6练习(4)中诱导公式(1)的逆用，连老师也采用直接讲授的方式.这在以自主学习为主调的课堂上，呈现“当讲则讲”的两个教学片断，更显难能可贵.

4　结束语

客观地说，连春兴老师的授课风格与我们平时授课有一定差异，为了解同行对这种差异的认识，我们组织了全校初、高中数学教师座谈会.会上，大家从如下几个角度给予连老师高度评价：

1.吸引——每一个问题都有的放矢，明确具体，引人思考.

2.台阶——每一个问题的解决都为下一个问题搭好台阶.

3.重构——不拘泥课本呈现方式，以最适宜学生参与自主学习的形式，呈现知识的发展脉络.

4.精炼——精炼的语言，准确的表述， 漂亮整洁的板书.

5.鼓励——微笑、期待的眼神，让学生如沐春风.

平心而论，连老师作为优秀的数学特级教师，已无需我们的溢美之词，但他厚积薄发，手持一根粉笔上讲堂，看似稀松平常，却处处智慧，表面信手拈来，却精彩纷呈，这正是值得我们由衷赞叹和学习的地方.特别是连老师通过一节课，深刻诠释了他诸多先进理念的实践途径，这对我们数学教师改善教学行为，实现专业发展，无疑将起到潜移默化的推动作用.