考虑风电不确定性的电气能源系统两阶段分布鲁棒协同调度

税　月, 刘俊勇, 高红均, 邱　高, 胥威汀, 苟　竞

(1. 四川大学电气信息学院, 四川省成都市 610065; 2. 国网四川省电力公司经济技术研究院, 四川省成都市 610000)

0　引言

近年来,随着“能源互联网”概念的提出,实现多能流间的相互转化成为国内外的研究热潮[1-2]。相比于其他一次能源,天然气具有清洁、环保的特征,研究其与电力系统间的相互影响具有实际意义。

国内外学者对以燃气轮机为耦合关联的电气综合系统协调规划和优化运行方面已取得了一些研究成果[3-5]。燃气轮机是将天然气转化为电力(气转电)的单向流动元件。近年来出现的电转气(P2G)技术可将电力系统中多余的清洁能源转化为氢气或天然气,从而有效地消纳清洁能源[6-10],形成双向闭环流动的电气综合系统。文献[11-12]研究了含P2G装置和风电的电气综合系统调度问题,但都未考虑风电出力的不确定性对综合能源系统协调优化的影响。

文献[13-14]分别采用了基于场景和鲁棒优化的方法处理电气综合系统中的风电不确定性问题,但以上两种不确定性处理方法均存在各自的局限性。随机优化方法通过概率分布进行描述,计算量较大,同时在实际中较难获得准确的概率分布,可能导致模型不够精确[15]。鲁棒优化算法以不确定性因素的边界参数表征,往往难以选取合适的鲁棒集合,决策结果偏保守[16]。近年来,国内外学者尝试采用分布式鲁棒优化方法(DRO)[17-18]处理不确定性问题,该方法将随机规划和鲁棒优化方法相结合,在满足不确定性参数信息条件下寻找最恶劣的概率分布函数,但该方法的求解过程过于复杂[19]。因此,本文采用另一种基于数据驱动下的分布式鲁棒优化算法,通过获取不确定性参数的历史数据,建立范数约束条件约束不确定概率分布集合,从中制定出最恶劣概率分布下的决策方案。文献[20]和文献[21]分别将该方法应用到无功优化和机组组合问题中,但均以1-范数或∞-范数作为约束条件单独分析和优化,使得优化结果偏于片面和极端,同时考虑到实际中调度员需要确定唯一的调度方案,因此,本文将两种范数条件相结合,采用综合范数约束不确定性分布置信范围,应用于电气能源系统优化调度。

此外,文献[22-24]建立的两阶段调度模型中都仅传递了机组开停机状态变量,并未将机组出力值相关联。而在实际的调度中,调度员在日前安排机组启停计划、机组出力值等,实时运行则在此基础上采取一定调整措施以满足实时供需平衡[25-26]。基于此,本文建立了两阶段优化调度模型,将日前调度中的机组开停机状态和机组计划出力等变量与实时运行阶段相关联,通过机组出力调整、天然气气源供气调整来应对实时运行中的风电出力不确定性。

综上,本文充分考虑了风电不确定性,建立了基于数据驱动下的两阶段分布式鲁棒优化调度模型。模型的第一阶段考虑了电气综合系统总成本和风电预测信息下的弃风成本,制定出更经济的日前调度计划。模型的第二阶段在实时运行场景下,综合考虑1-范数和∞-范数条件约束不确定性概率分布置信集合,并涉及绝对值约束条件的等效线性化处理方法。此外,模型还考虑了天然气网的网络约束条件,并进行线性化处理,从而使得整体模型可以在混合整数线性规划框架下进行快速求解。最后,通过算例验证了分布式鲁棒优化算法的有效性。

1　基于数据驱动的分布鲁棒优化调度模型

电气能源系统包含了电力系统侧和天然气系统侧,并以燃气轮机机组和P2G装置为耦合元件,形成电气能源双向转化的闭合流动方式。详细系统结构图参见附录A图A1。

1.1　目标函数

在进行电气能源系统经济协调调度时,以日前经济调度成本和实时运行下的调整成本之和最小为目标函数:

(1)

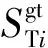
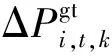
式(1)的第一部分表示综合系统日前经济调度总成本,包括常规机组启停机成本和运行成本、燃气轮机机组启停机成本和运行成本、弃风成本三个部分;第二部分表示在实时调度中,考虑风电出力不确定性下,综合系统各机组和各装置进行出力调整而产生的调整总成本。

可以看出,式(1)为一个min-max-min的三层两阶段优化问题,与传统两阶段鲁棒优化不同的是,传统鲁棒优化仅仅优化最恶劣场景问题,而分布鲁棒优化模型的内层的max-min函数通过求解决策变量{pk},寻找K个离散场景的最恶劣概率分布情况,进而获得其期望成本的最大值。

本文提出的“数据驱动”算法是以风电历史数据作为参考,用于表征风电出力的不确定性,具体是通过提取调度系统可用的M个典型日(以1 h为时间步长的24个离散出力值)风电出力历史数据,筛选出K个离散场景下的风电出力值(ξ1,ξ2,…,ξK),并由此获得每个离散场景的初始概率值,考虑到各离散场景概率分布的不确定性,进一步以初始概率分布值为中心,综合范数条件为约束进行优化求解,获得各离散场景的最恶劣概率分布值,详细模型可参见1.4节。

1.2　预测信息下约束条件

基于预测信息下的日前经济调度约束条件包括电网约束、天然气网络约束和耦合元件约束条件。

1.2.1电网约束条件

1)功率平衡

(2)

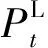
2)常规机组约束

(3)

(4)

(5)

(6)

(7)

(8)

yi,t-zi,t=Ii,t-Ii,t-1

(9)

yi,t+zi,t≤1

(10)

Ii,tPi,min≤Pi,t≤Ii,tPi,max

(11)

(12)

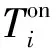
3)风电机组出力约束

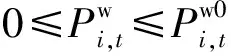
(13)

4)潮流约束

本文采用文献[27]中的直流潮流约束,支路潮流应满足:

(14)

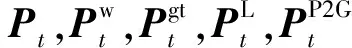
4)备用约束

电气系统中通过常规机组和燃气轮机机组提供正、负备用:

(15)

(16)

式中:rwind为风电的旋转备用率,取10%。

1.2.2天然气网络约束条件

1)节点气压约束

在天然气网络中,每个节点都有压力上下限值:

πi,min≤πi,t≤πi,max

(17)

式中:πi,t第i个节点t时刻的气压;πi,min和πi,max分别为压力的下限、上限值。

2)质量守恒定律约束

天然气管网中的天然气流量需要满足质量守恒定律,即是任意节点的总流入量等于总流出量。

(18)

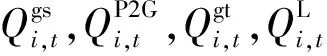
3)天然气系统潮流约束

对任意管道的管道流量与节点压力需满足以下关系:

(19)

式中:Cij为由管道摩擦力、温度、平均压缩因子等决定的综合参数;sgn(πi,πj)表示管道的流动方向,定义为

(20)

4)气源注入量约束

对于天然气气源的供气量需满足以下约束条件:

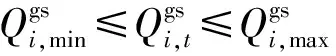
(21)

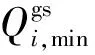
1.2.3耦合元件约束条件

综合系统中考虑燃气轮机机组和P2G装置作为电力系统和天然气系统间的耦合元件。

1)燃气轮机机组

(22)

(23)

(24)

(25)

式中:Qi,min和Qi,max分别为燃气轮机机组用气量的下限和上限;η为燃气轮机发电效率,取40%。燃气轮机机组的最小开停机时间约束同式(3)至式(8)。

2)P2G装置

(26)

(27)

式中:ηP2G为P2G装置的转换效率,本文取80%。

1.3　实时调度下约束条件

为应对风电出力的不确定性,在电气能源系统的实时运行阶段,需要调整常规机组出力、燃气轮机机组出力以及天然气气源的出力。

1.3.1电网约束条件

1)功率平衡

(28)

2)常规机组约束

Ii,tPi,min≤Pi,t+ΔPi,t,k≤Ii,tPi,max

(29)

(30)

3)风电机组出力约束

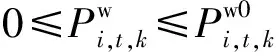
(31)

4)潮流约束

(32)

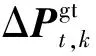
1.3.2天然气网络约束条件

1)节点气压约束

πi,min≤πi,t+Δπi,t,k≤πi,max

(33)

式中:Δπi,t,k为第k个场景下节点i在t时刻的气压变化值。

2)质量守恒定律约束

(34)

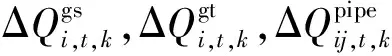
3)天然气系统潮流约束

(35)

4)气源注入量约束

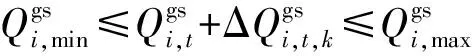
(36)

1.3.3耦合元件约束条件

1)燃气轮机机组

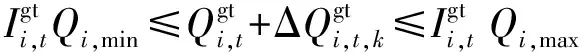
(37)

(38)

2)P2G装置

(39)

(40)

1.4　综合范数约束条件

在本文的两阶段分布鲁棒优化模型中,需要寻找使期望目标函数值最大的场景概率分布值,而在求解过程中,为使得所求取的概率分布值与实际运行数据相贴近,本文构建了以初始概率分布值为中心,以包含1-范数和∞-范数的综合范数为约束条件对离散风电场景的概率分布值进行约束,其可行域分别为Ω1和Ω∞。

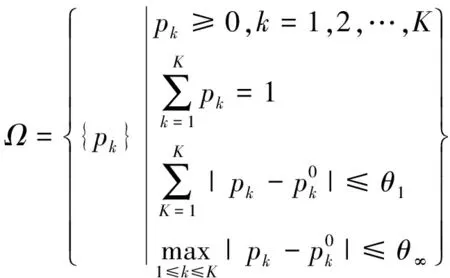
(41)

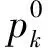
由文献[20-21]可知,{pk}满足如下的置信度:

(42)

令上不等式右边分别为概率分布值的置信度α1和α∞,则可将式(42)转为式(43):

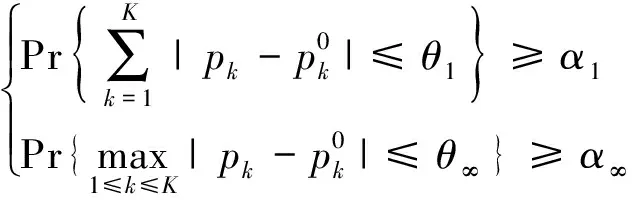
(43)

由式(42)和式(43)可得式(44)为:

(44)

式(1)至式(44)即为本文所提出的电气能源系统两阶段分布式鲁棒协同调度优化模型。

2　模型求解算法

2.1　模型线性化处理

2.1.1综合范数约束条件的线性化处理

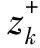
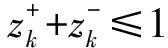
(45)

(46)

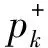
从而将原绝对值约束条件转换为:

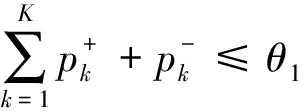
(47)

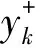
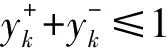
(48)

(49)

同样将原绝对值约束条件转换为:

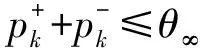
(50)

2.1.2天然气潮流的线性化处理

由于天然气潮流约束条件为非线性约束,需将其进行线性化处理。

首先,考虑到管道流量的流动方向具有唯一性,通过引入0-1辅助变量:

uij+uji≤1

(51)

式中:uij表示流量从节点i流向节点j;uji表示流量从节点j流向节点i。

式(20)中的方向变量可转化为:

sgn(πi,πj)=uij-uji

(52)

将式(19)的两边分别进行平方处理,可以得到:

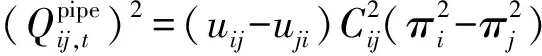
(53)

当管道流量流动方向为从节点i到节点j时,即式(53)可表示为:

(54)

(55)

同样地,对于管道流动方向从j到i时的处理方式相同。

2.1.3发电机成本函数线性化处理

由于综合系统模型式(1)中常规机组和燃气轮机组的发电成本为二次凸函数,本文采用参考文献[28]中的分段线性化方法将其分别转化。

因此,通过以上线性化处理方法,模型就可以转换为混合整数线性规划问题,并采用现有的求解工具包(如CPLEX)进行计算。

2.2　两阶段分布鲁棒模型求解

本文构建的基于数据驱动下的两阶段分布鲁棒优化调度模型,在模型的第一阶段针对综合系统的机组启停计划、机组计划出力值、天然气气源计划供气量、P2G装置用电量等鲁棒决策变量进行日前决策。模型的第二阶段根据实际风电出力,求取实时运行下的机组出力调整量、天然气气源供气调整量,以应对不同的风电出力场景。

针对所提出的两阶段模型,一般采用分解算法进行求解,现有广泛采用的分解算法有Benders分解算法和列与约束生成(CCG)算法[20]。本文采用CCG算法将模型分解为主问题(MP)和子问题(SP)进行反复迭代求解。其中,主问题在已知的恶劣概率分布下求解满足约束条件的最优解,进行综合系统的日前调度,并且为式(1)提供下界值:

(56)

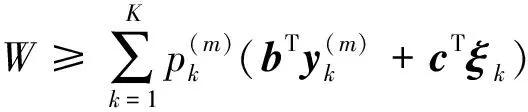
(57)

式中:x为第一阶段鲁棒决策变量;yk为第k个场景下第二阶段变量;y0为风电预测场景下的第二阶段变量;ξ0为风电预测出力值;ξk为第k个离散场景下的风电出力值;m为迭代次数。式(57)即是式(1)中的第二部分。

子问题是在主问题给定的变量x下,寻找实时运行下的最恶劣概率分布,并返回给主问题以供下一次迭代使用,为式(1)提供上界值:

(58)

在式(58)中的内层min函数中,各场景问题相互独立,可采用并行求解的方法进行处理,并表示为f(x*,ξk),从而将式(58)改写为:

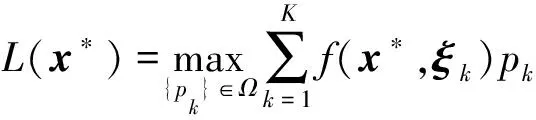
(59)

综上,式(1)的两阶段模型通过式(56)和式(57)及式(59)间的不断迭代与变量更新,直到达到给定精度值,停止迭代。

3　算例分析

3.1　算例系统构成

本算例选取修改后的IEEE 39节点系统和根据文献[11]修改后的6节点天然气系统,天然气系统结构图参见附录A图A2。附录A图A3中给出了风电预测出力和电、气负荷数据。燃气轮机和常规机组及P2G装置的相关数据均在附录A表A1至表A3中给出。

3.2　数据驱动下的分布鲁棒优化调度结果及相关对比分析

本节计及风电出力不确定性,通过电气综合系统的日前调度和实时运行两阶段调度的结果分析对比,验证本文提出的基于数据驱动的分布鲁棒优化算法的有效性。

3.2.1不同历史数据个数下结果对比

本节验证在式(44)中选取不同历史数据个数时的结果对比。其中,设置信度水平α1和α∞均为0.5,离散场景K设为10。以风电历史数据个数从100到10 000进行计算。同时,采用随机规划方法在10 000个历史数据下进行模拟计算,并与本文算法进行对比,如表1所示。

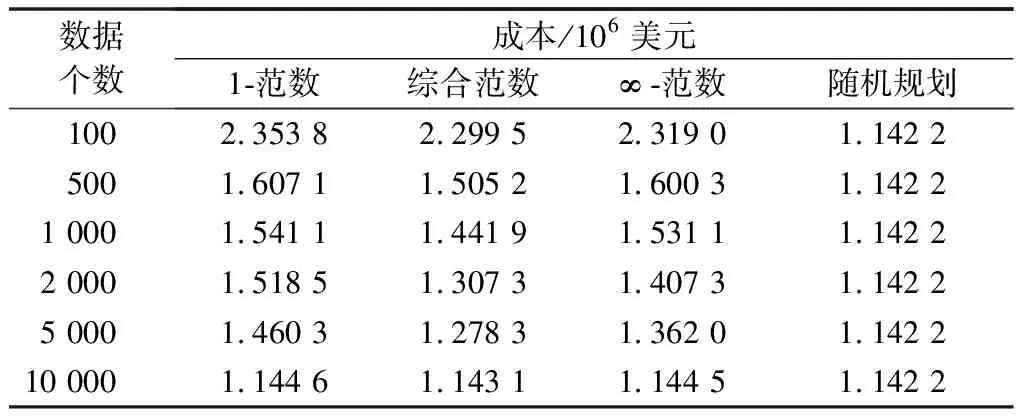
表1　不同历史数据个数时的结果对比Table 1　Result comparison under different numbers of historical data

表1展示了不同历史数据个数下,电气综合系统的日前调度和实时调整总成本结果。可以看出,随着历史数据的增大,总成本值在逐渐降低,这是由于历史数据个数的增大,使得概率分布函数的允许偏差值减小,从而降低了求解问题的保守度。同时由计算结果可以看出,本文提出的综合范数约束条件在相同历史数据个数条件下,相较于另外两种约束条件的总成本值更低,这说明了本文模型的保守度更低。

在与传统随机规划方法进行对比时可以看出,随着历史数据个数的增加,分布鲁棒算法的成本值与随机规划结果越接近,即保守度越低。为保证综合系统的鲁棒性,在之后的计算中均采用历史数据个数为1 000进行计算。

3.2.2不同置信区间下结果对比

本节通过设置不同的置信区间α1和α∞对电气综合系统的计算结果进行分析。其中,历史数据个数均为1 000,离散场景K均为10,结果如表2所示。

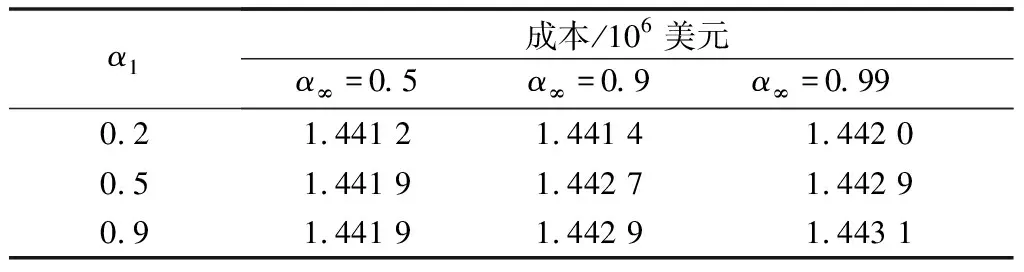
表2　不同置信水平下结果对比Table 2　Result comparison under different confidence sets

通过表2可以看出,随着置信区间取值的增大,综合系统总成本值也在增大,这是因为随着置信区间的增大,求解问题所包含的风电出力不确定性增大,系统需要调用更多的机组加以应对,故综合总成本增加。这也与式(44)中的规律相一致,证明了计算结果的正确性。

进一步,选取α∞为0.99,α1分别为0.2,0.5和0.9的综合范数约束下的计算结果与α∞为0.99下仅考虑∞-范数的计算结果对比,如表3所示。由计算结果看出,综合范数约束条件由于综合考虑了1-范数,其计算结果较∞-范数更低,即保守度更低。

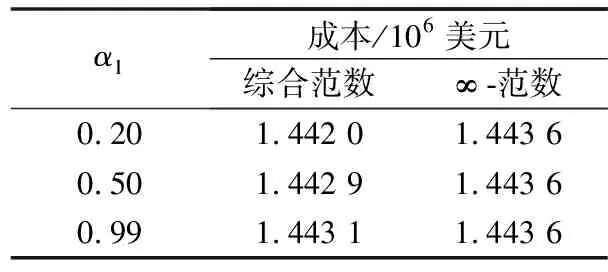
表3　综合范数与∞-范数结果对比Table 3　Result comparison between comprehensive norm and ∞-norm

选取α1为0.5,α∞分别为0.5,0.9和0.99的综合范数约束条件下的计算结果与α1为0.5的1-范数约束下的计算结果进行对比,如表4所示。可以看出,同样地,综合范数约束条件下的总成本值较仅考虑1-范数约束条件下的更低,保守度更低。

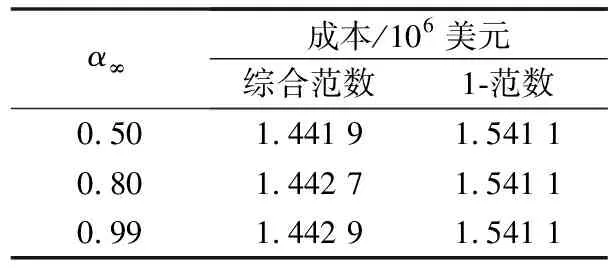
表4　综合范数与1-范数结果对比Table 4　Result comparison between comprehensive norm and 1-norm

3.2.3不同不确定性方法下结果对比

为证明本文所提出算法的有效性和正确性,本小节通过与传统的随机规划方法和鲁棒优化算法进行计算结果对比分析。首先,通过第一阶段优化求解出日前调度的决策变量,然后再随机生成10 000个概率分布场景值进行调整成本期望值对比测试分析。其中,分布式鲁棒优化算法的参数选取分别为:置信度水平α1为0.5,α∞分别为0.5,0.9和0.99,历史数据个数为1 000,离散场景为10。计算结果如表5所示。

表5　不同算法结果对比Table 5　Results comparison between different algorithms

由表5的计算结果可知,分布鲁棒优化算法在求解电气能源系统两阶段调度模型时,在第一阶段的总成本值介于传统的随机规划方法和鲁棒方法之间,即说明相对于随机规划方法而言,本文算法的鲁棒性更强,通过调整机组出力和天然气供气量以应对综合系统中的风电不确定性,而相对于只考虑恶劣风电场景信息下的传统鲁棒算法而言,则具有更好的经济性。在10 000个概率分布测试期望值的结果中,本文方法的均值和最大值均低于另外两种方法,说明其概率分布平均性能和最恶劣概率分布性能均优于另两种方法,其经济性更优。综合来看,本文提出的分布鲁棒算法在经济性和鲁棒性之间取得了均衡。

4　结论

本文考虑了风电出力不确定性,对以燃气轮机机组和P2G装置为耦合元件的电气能源系统建立了两阶段分布式鲁棒优化调度模型,所得结论如下。

1)本文提出的基于数据驱动下的两阶段分布鲁棒优化算法的计算结果与所选历史数据、置信区间有关。其中,所选历史数据个数越多,算法保守度越低;置信区间越大,算法保守度越高。

2)综合考虑1-范数和∞-范数约束条件下的分布鲁棒优化算法相较于只考虑1-范数和只考虑∞-范数约束下的计算结果更具经济性。

3)分布鲁棒优化算法将随机规划和传统鲁棒优化算法相结合,较随机规划而言鲁棒性更强,较传统鲁棒算法而言经济性更好。

需要指出的是,本文集中采用两阶段分布式鲁棒优化方法对电气能源系统中的风电不确定性建模,下一步工作将研究不同规模仿真系统下的算法求解效率等问题。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。