竞赛图的超生成连通性

张云霞， 张　博， 杨卫华

(1. 山西省财政税务专科学校 公共课教学部， 山西 太原 030024； 2. 太原理工大学 数学学院， 山西 太原 030024)

0　引　言

本文未明确介绍的术语, 见参考文献[1-2]. 一个有向图D是由顶点集V(D)和弧集A(D)构成, 如果xy是D的一条弧, 则称x控制(指向)y. 如果A和B是顶点集V(D)的子集合且A中的每个顶点控制(指向)B中的每个顶点, 则称A控制(指向)B. 在有向图中, 一条有向路P是一条点序列v1,v2,…,vk, 其中vivi+1是对所有i=1,2,…,k-1 的弧 (本节所有的路均指有向路). 顶点v1被称为路P的起点, 顶点vk被称为路P的终点. 路P的长度等于路中弧的数目, 即|P|-1. 顶点v2,v3,…,vk-1被称为路P的内部点或中间点. 如果两条路的内部顶点不相同， 称之为内部不相交的两条路. 如果x和y是D的两个顶点,P是从x到y的一条有向路, 称P是一条(x,y)-路.如果uv∈A(D)且P是一条长度为k≥2的(u,v)-路, 则P被称为弧uv的k-支路(即k-bypass).

竞赛图T是任意两点之间恰有一条弧的有向图. 竞赛图T的一条哈密尔顿路(resp. 圈)是一条包含T中所有顶点的路(resp. 圈). 如果在有向图D中任意两个顶点x和y之间, 有从x到y的哈密尔顿路或者从y到x的哈密尔顿路, 则称D是弱哈密尔顿连通的; 如果在有向图D中任意两个顶点x和y之间, 都有从x到y的哈密尔顿路和从y到x的哈密尔顿路, 则称D是强哈密尔顿连通的.

在有向图D中, 任意两点x和y之间都存在一条(x,y)-路和一条(y,x)-路， 则称D是强连通的(或称为强的). 如果在有向图D中任意删除少于k个顶点的点集后, 有向图仍是强连通的, 则称D是k-强连通的(或称为k-强的). 在图论中, 连通性是最基本的内容之一, 许多重要的理论都与它相关, 其中就有重要的Menger’s定理[3](点连通性)： 有向图D是k-强连通的(或称为k-强的)当且仅当对于D中任意两个顶点x和y, 都有k条内部不相交的路从x到y且有k条内部不相交的路从y到x.

在无向图G中,u和v之间的一个k-container,C(u,v)是u和v之间k条内部不相交的路的集合. 图中container的概念是由Hsu[4]提出的, 并用于评估互连网络的通信性能. 如果k-container,C(u,v)包含了G中所有的顶点, 则称它是一个k*-container. 如果G的任意两个不同顶点之间存在一个k*-container, 则图G是k*-连通的. 由Albert[5]等人提出的全局3*-连通图是对k*-连通图的研究. 显然, 图中的生成连通性也是哈密尔顿连通性的推广.

许多学者已对无向图的生成连通性进行了研究. 例如, Lin[6]等证明了饼图Pn是w*-连通的当且仅当n≥3, 其中1≤w≤n-1. Lin[7]等人还给出了图是r*-连通的充分条件， 他们证明了对于图G中任何两个不相邻的顶点u和v, 如果dG(u)+dG(v)≥|V|+k, 则G是r*-连通的， 其中r∈{1,2,…,k+2} (k是正整数). 文献[8-9]分别讨论了无向图的生成连通性和无向图的生成扇形连通性. 文献[10-11]分别讨论了线图的生成连通性和图的势的生成连通性. 文献[12]讨论了排列图的生成连通性. 文献[13-15]还讨论了生成连通性的一些广泛性质.

有关有向图的生成连通性方面， Thomassen[16]研究了竞赛图的弱哈密尔顿连通性和竞赛图的强哈密尔顿连通性. 同时， 人们已经在弱哈密尔顿连通性的基础上推广并定义了有向图的生成连通性. 本文将在强哈密尔顿连通性的基础上推广并定义有向图的超生成连通性.

令D是一个有向图,u和v是D中任意两个顶点. 在有向图D中,u和v之间的一个k-container是u和v之间有k条内部不相交的路的集合， 如图 1 所示.

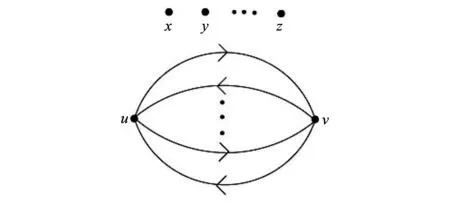
图 1　u和v之间的k-containerFig.1　k-container between u and v

如果k-container包含D中所有的点， 则它被称为k*-container. 如果从u到v有k条内部不相交的且方向相同的路的集合, 并且它们包含D中所有的顶点, 则k-container是从u到v的强k*-container， 如图 2 所示.

图 2　从u到v的强k*-containerFig.2　Strong k*-container from u to v

1　预备知识

定理1[3]令D是有向图且x和y分别是D的任意两个顶点, 则D是k-强连通的(或者称为k-强的)当且仅当D既包含k条从x到y的内部不相交的路, 同时也包含k条从y到x的内部不相交的路.

引理1[16]令T是竞赛图,x和y分别是D的任意两个顶点. 如果T有三条内部不相交且长度至少为2的(x,y)-路, 则T有一条哈密尔顿(x,y)-路.

引理2[16]如果e是 3-强竞赛图T的一条弧, 则e被包含在的哈密尔顿圈中.

Thomassen[16]已经证明4-强连通竞赛图的每条弧都有一个哈密尔顿支路 (即: 4-强连通竞赛图的任何两点x,y之间, 都既有一条哈密尔顿路从x到y, 又有一条哈密尔顿路从y到x). 根据该结果, 可以得到下面的结论.

引理3[16]4-强的竞赛图是超强1*-连通的.

引理44-强的竞赛图是超强2*-连通的.

证明令T是4-强连通竞赛图,x和y分别是T的任意两个顶点. 不失一般性, 假设xy∈A(T), 则根据引理3, 弧xy有一条哈密尔顿支路, 即x从y到有一个强的2*-container. 下面只需证明y从x到有一个强的2*-container.

T-{x,y}的点可以被划分成4个集合A,B,C,D, 它们满足以下条件:

1)x和y都控制集合A中的每个点;

2)x和y都被集合B中的每个点控制;

3)x控制集合C中的每个点且集合C中的每个点控制y;

4)y控制集合D中的每个点且集合D中的每个点控制x.

下面考虑两种情形.

情形1|D|=φ. 由于T是4-强连通竞赛图, 根据定理1, 至少有4条弧从集合A指向集合B且这些弧两两不相交. 用u1v1,u2v2,u3v3和u4v4来表示这4条弧, 其中ui∈A,vi∈B且i∈{1,2,3,4}, 则x和y之间至少有4条长为3的(y,x)-路. 删除(y,x) -路中的内部顶点u1和v1, 则删除点后得到的竞赛图是2-强连通的且有3条内部不相交且长度为3的(y,x)-路. 根据引理1, 这个竞赛图有一条哈密尔顿(y,x)-路. 再加上路yu1v1x, 则从y到x有一个强的2*-container.

情形2|D|≥1. 在T中至少有一条长为2的(y,x)-路, 删除(y,x)-路中的内部顶点, 则得到的竞赛图是3-强连通的. 由于x控制(指向)y, 根据引理2, 这个竞赛图有一条哈密尔顿(y,x)-路. 再加上长为2的(y,x)-路, 则y从x到有一个强的2*-container.

因此, 竞赛图T从x到y和从y到x都有一个强的2*-container, 所以,T是超强2*-连通的. 证毕.

2　主要结果

下面给出本文的主要结论：

定理2对于所有的k≥2, 一个2k-强连通的竞赛图是r*-强连通的 (1≤r≤k).

证明当k=2时, 根据引理3和引理4,T是超强1*-连通的和超强2*-连通的. 下面考虑k≥3 的情况. 令T是2k-强连通竞赛图,x和y分别是T中任意两个顶点.T-{x,y} 的点可以被划分成4个集合A,B,C,D, 它们满足以下条件:

1)x和y都控制集合A中的每个点;

2)x和y都被集合B中的每个点控制;

3)x控制集合C中的每个点且集合C中的每个点控制y;

4)y控制集合D中的每个点且集合D中的每个点控制x.

假设min{|C|,|D|}=m， 则T有m条内部不相交的长为2的(x,y)-路和m条内部不相交的长为2的(y,x)-路. 下面考虑两种情形.

情形30≤m≤k-1. 由于T是2k-强连通竞赛图, 根据定理1, 至少有2k-1-m条弧从集合A指向集合B且这些弧两两不相交, 则x和y之间至少有2k-1-m条内部不相交的长为3的(x,y)-路 (也有2k-1-m条内部不相交的长为3的(y,x)-路). 从中选取s(1≤s≤k-2-m)条长为3的内部不相交的(x,y)-路, 令{P1,P2,…,Ps}表示这s条内部不相交的长为3的(x,y)-路, {Q1,Q2,…,Qm}(0≤m≤k-3)表示这m条内部不相交的长为2的(x,y)-路. 删除(x,y)-路中这2s个内部顶点且删除C中这m个内部顶点, 则得到的竞赛图(2k-2s-m)是-强连通的 (它至少是4-强连通的). 根据引理4, 这个竞赛图是超强2*-连通的. 因此, 从x到y有强的2*-container. 令{R1,R2}表示这两条内部不相交的(x,y)-路, 则{P1,P2,…,Ps,Q1,Q2,…,Qm,R1,R2}构成了从x到y的一个强的(s+m+2)*-container. 因为3≤s+m+2≤k, 则有从x到y的一个强的r*-container, 其中r∈{3,4,…,k}. 用相同的方法, 也可以得到y从x到的一个强的r*-container, 其中r∈{3,4,…,k}.

情形4m≥k-2. 在T中至少有k-2条长为2的内部不相交的(x,y)-路, 也至少有k-2条长为2的内部不相交的(y,x)-路, 从中选取s(1≤s≤k-2)条长为2的内部不相交的(x,y)-路, 令{P1,P2,…,Ps}表示这s条内部不相交的长为2的(x,y)-路. 删除长为2的(x,y)-路中的s个内部顶点, 得到的竞赛图是(2k-s)-强连通的 (它至少是4-强连通的). 根据引理4, 这个竞赛图是超强2*-连通的. 因此, 从x到y有强的2*-container. 令{R1,R2}表示这两条内部不相交的(x,y)-路, 则{P1,P2,…,Ps,R1,R2}构成了从x到y的一个强的(s+2)*-container. 因为3≤s+2≤k, 则有从x到y的一个强的r*-container, 其中r∈{3,4,…,k}. 用相同的方法, 也可以得到从y到x的一个强的r*-container, 其中r∈{3,4,…,k}.

因此,T有从x到y的一个强的r*-container和从y到x的一个强的r*-container, 则T是超强r*-连通的, 其中r∈{1,2,3,4,…,k}. 证毕.

由定理2, 有如下推论:

2018年 第39卷 第4期中 北 大 学 学 报(自然科学版)Vol.39 No.4 2018(总第180期)JOURNAL OF NORTH UNIVERSITY OF CHINA(NATURAL SCIENCE EDITION)(Sum No.180)