具有小修和不完全预防性维修的多状态退化系统的可靠度分析

王丽花

(包头师范学院 数学科学学院， 内蒙古 包头 014030)

0　引　言

在生产过程中， 大多数工作系统都会随着时间的增加和产生的损耗而逐步退化， 然后发生故障或完全失效. 这样的多状态退化系统模型几乎取代了二值状态模型， 且已有大量的研究， 然而针对该类多状态退化系统模型， 维修方式更具有研究意义， 比如故障前的不完全预防性维修、 故障后的更换策略、 泊松失效后的小修等. 可修的多状态退化系统模型是系统可靠性理论中非常重要的一类模型， 在电力、 网络等领域广为适用， 对于这类模型之前已有一些研究.

多状态退化系统的可靠性研究， 一个主要方面就是采用不同的方法对系统的可靠性进行分析和系统故障模型的建立. 1989年， Wang 和Sivazlian[1]研究了具有m个部件、s个温贮备和R个修理工的可修系统的可靠性指标， 得到了可靠度和首次故障前的平均时间的表达式. 武月琴等[2]对n中连续取k系统进行了研究. Kai[3]也研究了如何将二值状态系统故障树推广到多状态系统的问题， 并编程实现了多状态故障树的定量分析. Ushakov[4]提出了通用衍生函数法. Veeraraghavan和Trivedi[5]提出了一个容纳一排斥(Inclusion-Exclusion)公式， 得到了状态概率的表达式. Zang和Trivedi[6]给出了二态决策图法， 将多状态元件状态用一个布尔变量来表示， 整个系统的行为用一系列的多状态故障树来表示. Levitin[7]利用通用生成函数方法计算了多状态串-并联系统可靠性， 从而为多状态系统可靠性优化设计提供了基础. Zio等[8]利用Monte Carlo仿真方法评估了可重构多状态系统的可用度. Isaac W. Soro等[9]研究了具有小修和不完全预防性维修的多状态退化系统， 但只给出了状态概率的微分方程组， 以及一些性能指标的简单结果. 文献[10]中也对多状态退化系统模型进行了研究， 且采取了小修和一般型更换策略的维修模式， 得到了一些重要的可靠性指标. Huan Yu等[11]也对可修的多状态退化系统作了更深的研究， 提出了一种新的计算可用度的方法. 随着不同维修模式和不同研究方法的出现， 系统的可靠性理论逐步真正用于了指导实际问题. 最新的研究里， 充分将多状态系统的可靠性分析与数理统计学、 代数学、 电子学等联系了起来， 且利用其中的知识对多状态退化系统模型的可靠性分析作出了解答. Hu and Yue等[12]对一种可修的多状态串并联系统进行了可用度的等价分析， 并得到了两种等价因素. Peng Di等[13]对一种将通用生成函数与PH分布相结合的多状态系统的可靠性进行了分析， 得到了可靠度指标、 系统瞬时可用度和平均性能率指标等. 2018年， 王涛等人[14]将多状态系统的理论引入到阵列的可靠性分析中， 采用通用生成函数方法建立了阵列的可靠性分析模型. 米金华等[15]借助贝叶斯网络对多状态系统的图形表达和推理优势， 采用模糊理论中区间值三角模糊数对部件概率进行描述， 从而提出基于区间值模糊贝叶斯网络的复杂多状态系统可靠性分析的方法.

本文采用代数中矩阵部分的Crammer法则及Laplace反演得到系统状态转移概率， 从而得到可靠度重要指标.

1　模型描述

起初系统是新的， 处于正常工作状态， 然后系统逐渐退化， 当退化到完全失效时， 受到不完全预防性维修， 使系统恢复到工作时任一状态； 在退化过程中， 系统有可能随时泊松失效， 然后得到小修， 使系统恢复到先前的退化状态. 图 1 为系统的状态转移图.

图 1　系统状态概率转移图Fig.1　System state transition diagram

系统一共有2d+1个状态， 状态归为四类： 全新状态(状态1)； 退化状态(状态(2j-1)j=2,3,…,d)； 泊松失效状态(状态(2j)j=1,2,…,d)； 完全失效状态(状态(2d+1)).

四种参数表示的意义分别为：

λj： 从状态(2j-1)到状态(2j)的失效率或者转移率；j=1,2,…,d;

μj： 从状态(2j)到状态(2j-1)的小修修复率或者转移率；j=1,2,…,d;

αj： 从状态(2j-1)到状态(2j+1)的退化率或者转移率；j=1,2,…,d;

βj： 从状态(2d+1)到状态(2j-1)的转移率.j=1,2,…,d-1.

注： 为了求系统的可靠度R(t)， 令系统的所有失效状态为马尔可夫过程的吸收状态， 即系统一旦进入泊松失效状态2j(j=1,2,…,d)和完全失效状态2d+1， 就永久留在该状态.

定理1系统可靠度的Laplace变换式为

(1)

证明线性微分方程组如下

(2)

j=2,3,…,d.

（3s)

初始条件：P1(0)=1，P2j-1(0)=0;j=2,3,…,d.

对上述方程组作Laplace变换得

(4)

j=2,3,…,d.

（5)

方程组的Laplace式可写成如下矩阵形式

AP=B,

其中，

B=(1,0,0,…,0,0,0)T.

解析过程： 根据Cramer法则[16]， 得到

(6)

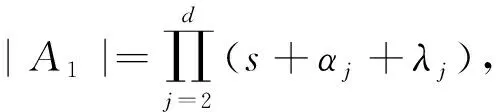
（7)

（8)

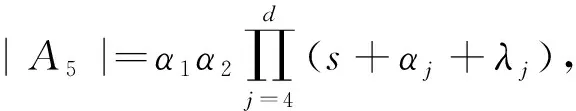
（9)

…

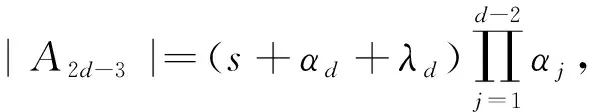
（10)

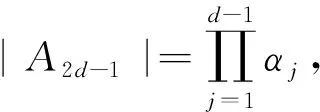
（11)

式中： |A2j-1|为矩阵A中的第j列换为B中元素后得到的矩阵所对应的行列式. 所以由式(6)～式(11)可得

(12)

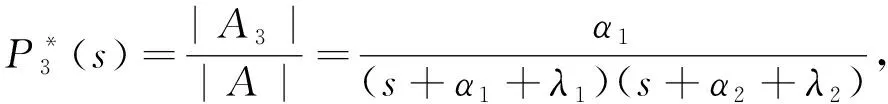
（13)

（14)

…

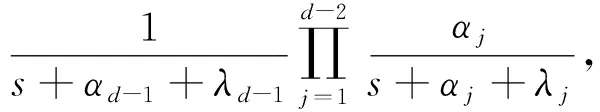
（15)

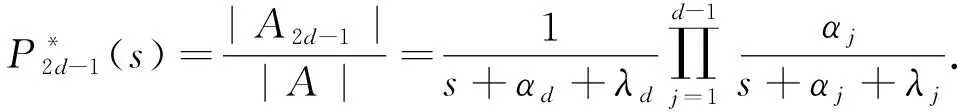
（16)

根据Laplace反演法， 将式(12)～式(16)反演可得

P1(t)=e-(α1+λ1)t,

P5(t)=

…

所以， 系统可靠度

得到定理所示形式.

2　结　语

本文研究了具有实际意义的多状态退化系统， 并且为减少失效率与退化率而采用不完全预防性维修和小修的情况下计算了其可靠度. 另外， 还可以作出进一步的推广或者研究， 假定多状态退化系统为广义几何过程模型， 修理设备数不确定、 维修具有周期性等， 那么使得多状态退化系统的研究更加广泛和接近实际.