泵阀联合EHA鲁棒增益调度分级压力控制

刘　霄 ， 张　振 ， 李海军

(1. 烟台大学 计算机与控制工程学院， 山东 烟台 264006； 2. 海军航空大学 岸防兵学院， 山东 烟台 264001)

0　引　言

电静液作动器(EHA)具有易控制、 工作效率高和体积小等优点[1-3]， 国内外大量采用的EHA方案是“变转速电机+定量泵”方式， 但其无法满足大负载高响应系统的要求， 其主要原因是容积控制方式使得系统响应取决于电机及泵的响应， 文献[4]提出泵阀联合控制方案， 通过对泵源输出流量及泵源压力的合理调配， 不但其最大响应速度可以达到阀控响应， 而且其效率比传统阀控系统有较大提高. 但泵源压力的改变， 会使伺服阀的工作特性发生改变， 因此需要应用控制策略实时整定伺服阀控制参数. 文献[5]采用模糊PID控制算法对控制参数进行实时整定， 但没有考虑泵源压力大范围变化及系统模型参数发生变化时对系统性能的影响.

增益调度是一种有效解决大范围动态变化的控制方法， 目前对于增益调度控制主要分两个研究方向， 一个是基于LPV(线性变参数)的增益调度控制方法， 主要是基于LFT(线性分式变换)/H∞的小增益方法和基于Lyapunov函数/二次H∞性能方法[6-10]， 由于采用LMI(线性矩阵不等式)求解， 所设计控制器结构复杂， 不利于工程实现[11]； 另一个是传统增益调度控制方法， 它首先通过选择典型工作点， 针对工作点设计局部控制器， 然后通过插值来产生全局控制器[12-15]， 虽然它易于工程实现， 但工作量大且忽略了系统参数的时变性， 难以在所有有界参数变化范围内保证系统的稳定性. QFT(定量反馈理论)可保证系统在参数较大变化下的鲁棒性， 但是在范围很大的情况下， 靠单一控制器往往很难保证系统性能要求.

鉴于上述原因， 本文以泵阀联合EHA为对象， 将增益调度控制与QFT相结合， 以集合其两者的优点， 一方面QFT可以减少增益调度的工作量且弥补了其缺乏稳定性保证的缺陷； 另一方面增益调度可使得QFT在大范围变化下的控制性能仍然良好.

1　分级压力控制原理

目前机载作动系统泵源压力是按负载峰值压力确定的， 但根据相关研究表明[16]， 在一个典型飞行任务中， 飞机所需峰值压力时间仅占其飞行总时间的5%左右， 并得出了理想状态下各阶段所需泵源压力的参考值. 因此， 飞机在飞行过程中所需泵源压力并不是一层不变的， 如果使飞机泵源压力随不同飞行阶段而改变， 不仅可以提高作动系统效率， 还可以减少系统的发热.

图 1 表示了泵阀联合EHA分级压力控制原理. 作动器包含两套控制回路， 其中压力控制回路由永磁同步电动机、 定量泵和蓄能器组成； 位置控制回路由伺服阀和液压缸组成.

压力控制回路要实现对伺服阀前压力的控制， 需将指令压力与伺服阀前实际压力之间的压力差作为误差信号， 驱动电机减速或增速运转； 若要实现对负载位置的控制， 则须将位置控制回路中比较指令位置和负载实际位置之差作为误差信号， 控制伺服阀的流量. 通过压力控制回路来控制伺服阀前压力， 使其在不同飞行阶段而改变， 从而提高效率； 位置控制回路则发挥了阀控准确、 稳定和实时性高的特点.

图 1　泵阀联合分级压力控制原理图Fig.1　Composition principle of pump and valve combined EHA multistage pressure control

2　位置控制回路数学模型

泵阀联合EHA位置控制回路与传统液压控制回路相同， 主要由控制器、 伺服阀放大器、 伺服阀、 双向液压缸、 位移传感器和液压辅助部件组成.

假设伺服阀功率级结构为零开口四边滑阀且回油压力为零， 则阀的线性流量方程为

QL=Kqxv-KcPL,

（1)

式中：QL为通过伺服阀的流量， 即负载流量；Kq为伺服阀流量增益；xv为伺服阀阀芯位移；Kc为伺服阀流量—压力系数；PL为液压缸负载压力.

在式(1)中，Kq和Kc与泵源压力Ps有关， 可表示为

(2)

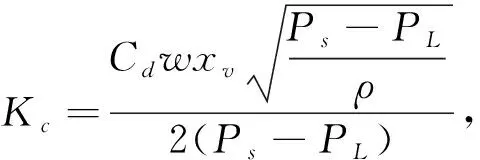
（3)

式中：Cd为滑阀阀口流量系数；w为滑阀的面积梯度；ρ为油液密度.

在忽略液压缸外部泄漏情况下， 其流量连续方程为

(4)

式中：A为液压缸液压杆活塞面积；xp为液压缸液压杆的位移；Ct为液压缸内泄漏系数；Vt为总压缩体积；βe为液压油有效体积弹性模量.

液压缸力平衡方程为

(5)

式中：Mt为液压缸液压杆及负载的等效总质量；Bt为液压缸液压杆及负载的等效阻尼系数和；FL为作用在液压杆的外负载力.

将式(1), (4)和(5)联合并进行拉氏变换， 得到阀芯位移xv作用时液压缸液压杆输出位移为

Xp=

（6)

式中：Kce为总流量-压力系数，Kce=Kc+Ct.

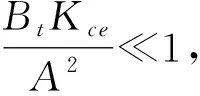
(7)

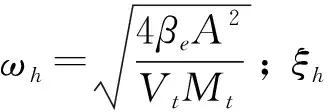
由式(2), (3)和(7)可以看出， 泵源压力的改变将使Kq和Kc发生改变， 从而使位置控制回路中的速度放大系数和液压阻尼比发生变化， 而速度放大系数直接影响系统的稳定性、 响应速度和精度， 液压阻尼比则影响系统的相对稳定性， 因此需要合适的控制策略使位置控制回路在不同泵源压力下的性能基本保持一致.

3　鲁棒增益调度控制器设计

根据增益调度控制思想， 按飞机飞行过程中理想状态下各阶段所需泵源压力划分为不同的工作模式， 每个工作模式下单独设计控制器， 同时为防止不同工作模式切换瞬间控制参数发生突变而导致系统不稳定， 应设计切换控制器， 来保证不同工作模式切换的平稳过渡.

3.1　改进PSO算法与QFT的融合控制器设计

QFT是一种频域设计方法， 它基于系统的不确定范围和性能指标来设计控制器且易于工程实现， 但它依赖于设计者的经验来对控制的结构和参数进行调试， 因此本文使用改进PSO(粒子群优化)进行参数优化后的PID控制器作为初始控制器， 在此基础上进行QFT控制器设计， 以克服最初的盲目性.

3.1.1改进PSO算法的PID控制器设计

PSO算法是一种基于群体智能方法的进化计算方法. 它可以描述为： 在D维的搜索空间中， 由n个粒子组成的种群X=(X1,X2,…,X3)， 其中第i个粒子在D维空间的位置可表示为Xi=(xi1,xi2,…,xiD)T. 根据目标函数可求出每个粒子位置对应的适应度值. 第i个粒子的速度为Vi=(Vi1,Vi2,…,ViD)T， 其个体极值为Pi=(Pi1,Pi2,…,PiD)T， 种群的群体极值为Pg=(Pg1,Pg2,…,PgD)T. 在每次迭代过程中， 粒子通过个体极值和群体极值更新自身的速度和位置， 即

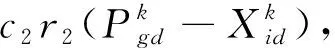
（8)

（9)

式中：d=1,2,…,D；i=1,2,…,n；w1为惯性权重；k为当前迭代次数；Vid为粒子速度；c1,c2为加速度因子， 通常取非负常数；r1,r2是分布在[0,1]区间的随机数.

由于PSO算法容易陷入局部最优， 有人提出局部PSO算法和动态惯性权重法[17]， 本文将集合三者的优点， 即在动态惯性权重PSO算法基础上， 利用全局最优加速收敛， 同时引入局部平均值避免陷入局部最优. 设一个种群由m个粒子组成， 则它们的平均值为

(10)

改进PSO算法速度更新方程为

（11)

（12)

式中：c3为加速度因子， 通常取非负常数；r3是分布在[0,1]区间的随机数；w2为惯性权重；itermax为最大迭代次数.

改进PSO算法整定PID参数的思想是： 利用算法在未知参数的所有可行解中寻找最优解， 从而使定义的适应度函数最小. 为此， 定义目标函数为

（13)

式中：e(t)为系统误差.

目标函数确定后， 即满足约束条件时， 使目标函数最小的值所对应的控制器参数便是最优控制器参数.

3.1.2改进PSO算法与QFT的融合控制

在进行QFT控制器设计时， 要把控制对象转化为传递函数形式， 并考虑其参数不确定大小和性能指标制定边界的情况. 改进PSO算法与QFT融合设计控制器具体步骤如下：

1) 对象模板设计

将式(7)转换为传递函数形式为

(14)

在考虑参数不确定大小时， 本文主要考虑液压油弹性模量和液压缸的泄漏量的不确定性. 液压油弹性模量一般为5×108～1.5×109N/m2， 而液压缸的泄漏量与液压油动力粘度有关， 它们之间关系为

(15)

式中：Qlt为液压缸的泄漏量；μt0为液压缸内工作温度为t0时液压油的动力粘度；λ为液压油的粘温系数， 一般取λ=0.042 7.

从式(15)中可以看出， 液压缸在不同工作温度下其泄漏量是不同的， 因此在考虑泄漏量不确定时， 可等效为泄漏系数的不确定性， 因此等效泄漏系数可表示为

(16)

将式(15)和(16)代入式(14)中， 便可得到位置控制回路对象模板.

2) 性能指标设计

① 鲁棒稳定性

∀ω∈[0,150) rad/s,

（17)

式中：P为位置回路开环传递函数；G为所设计的控制器；Ws为性能指标， 其值越小， 系统稳定裕度越大. 它保证了系统Mg(min)=5.93 dB，MP(min)=59°.

② 鲁棒跟踪性能

设其上下边界为

∀ω∈[0,80) rad/s,

（18)

式中：Tu(jω),Tl(jω)分别为位置控制回路跟踪边界上下界，F为前置滤波器， 其作用是使位置控制回路的闭环阶跃响应曲线落在边界范围之内.

根据位置控制回路特性要求， 确定其上下边界为

(19)

（20)

③ 控制器G和前置滤波器F的设计

在位置控制回路传递函数中， 取参数变化的标称值作为控制对象， 用上文所述的改进PSO算法进行PID控制器设计， 将所得PID控制器作为初始控制器， 在Bode图上看其闭环频率响应是否在跟踪性能指标上下界区域中， 如不在， 此时在QFT框架下对其整形， 从而得到所求的控制器和前置滤波器F.

④ 设计结果验证

在QFT框架下进行控制器设计时选择的是某些特殊频率点， 因此在设计完控制器之后需要在要求频率范围内用更加密集的频率点对控制器进行性能指标验证.

3.2　模糊切换控制器设计

泵阀联合EHA位置控制回路为在不同泵源压力下保持性能基本一致， 要在不同工作模式下进行切换， 但在不同工作模式切换的瞬间， 控制量会发生不连续变化， 从而影响系统的动态品质， 为此， 引入模糊集以使不同工作模式的区域边界模糊化， 从而使切换平滑化.

设飞机在飞行过程中划分为n种工作模式， 每种工作模式下的控制器为Gi(i=1,2,…,n). 由于负载压力PL可连续测量且直接决定所应选择的工作模式， 因此选择PL作为模糊切换指标.

采用if-then模糊规则， 对n种工作模式有n个规则， 第i个规则如下

IfPLisMi

Thenu=ui(Gi),

其中，M是PL相对应的模糊集；u是控制输入量；ui为第i个工作模式下的控制器输出.

模糊切换控制器输出为

(21)

4　仿真校验

利用MATLAB / Simulink仿真工具箱， 将所设计的控制器进行仿真. 泵阀联合EHA采用双级压力控制， 其相关参数如下：Ps1=14 MPa，ps2=21 MPa，Vt=1.2×10-4m3，Cd=0.6，w=3×10-2m，ρ=900 kg/m3，Bt=8.8×10-5N/(m/s)，A=1.8×10-3m2，Mt=20 kg.

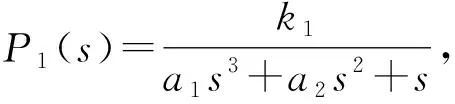
表 1　位置控制回路参数变化范围Tab.1　Parameter variety ranges of position control loop

取位置控制回路对象模版中参数标称值， 用改进PSO算法设计PID控制器， 选取种群总数为30， 最大迭代次数为100，c1=c2=1.2，c3=0.1，w2max=0.9，w2min=0.1， 将得到的PID控制器作为初始控制器， 其在Bode图上的闭环频率特性如图 2 所示.

图 2　PID控制器整形后的闭环频率响应Fig.2　Closed loop frequency response behind PID controller shaping

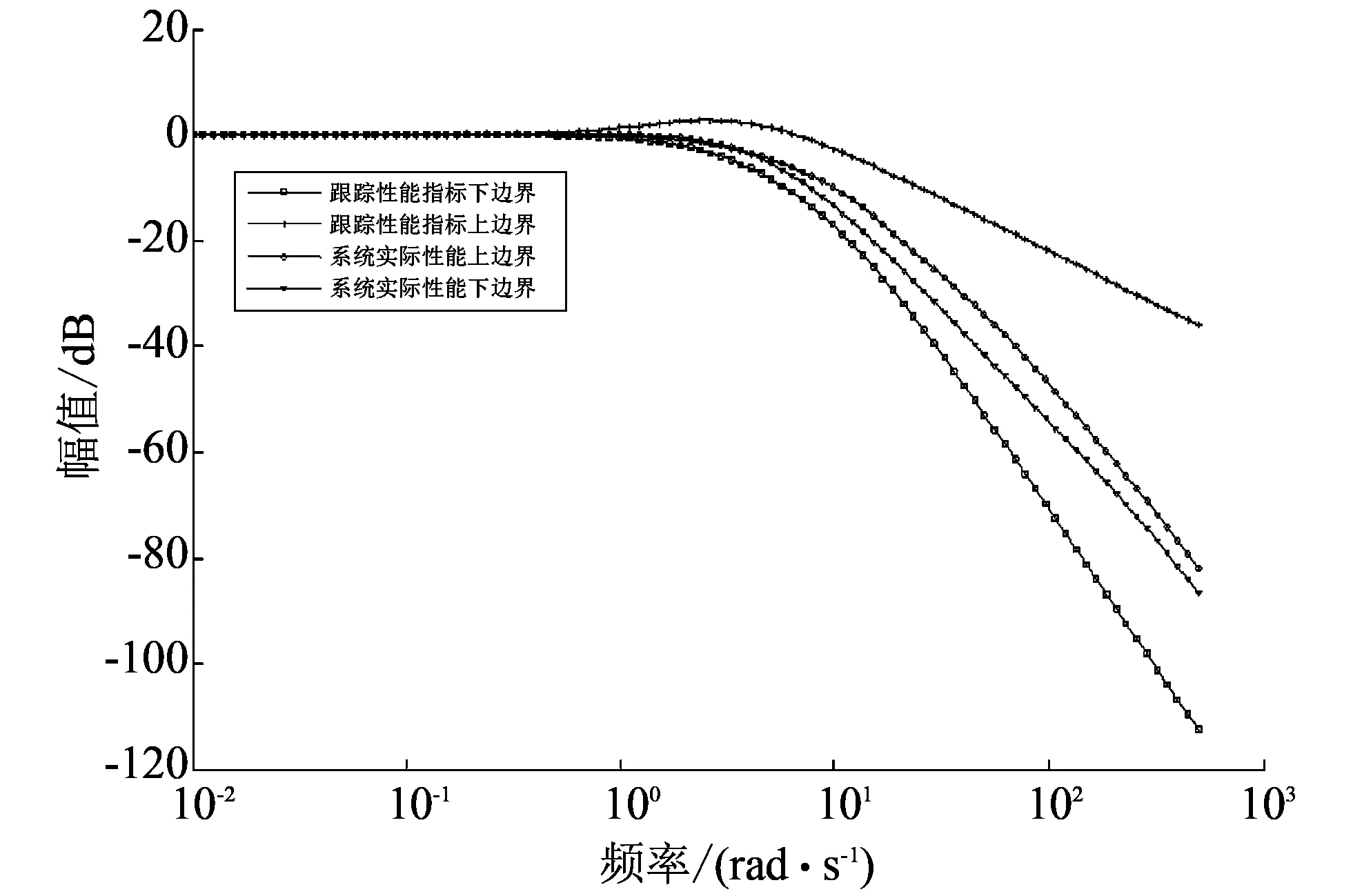
图 3　QFT对PID控制器整形后的闭环频率响应Fig.3　Closed loop frequency response behind QFT shaping to PID controller

从图 2 中可以看出， 由于系统参数的不确定性， PID控制器鲁棒控制性能较差， 因此系统实际性能并不在设定的性能指标边界内， 此时采用QFT对其进行设计， 经QFT设计后的系统闭环频率特性如图 3 所示， 由于QFT控制器可保证系统在参数较大变化下的鲁棒性， 从图中可以看出， 此时系统的闭环频率响应在性能指标边界之内.

同理在Ps2=21 MPa时， 依此设计控制器. 位置控制回路根据不同飞行阶段， 可在14 MPa和21 MPa的泵源压力下进行切换， 模糊切换过程中采用高斯隶属度函数.

图 4 为位置控制回路在鲁棒增益调度控制器下的阶跃响应， 从图中可以看出， 当泵源压力分别为14 MPa和21 MPa时， 位置控制回路性能基本一致， 说明本文所设计控制器有效， 实现了位置控制回路在不同泵源压力下增益基本保持一致的功能.

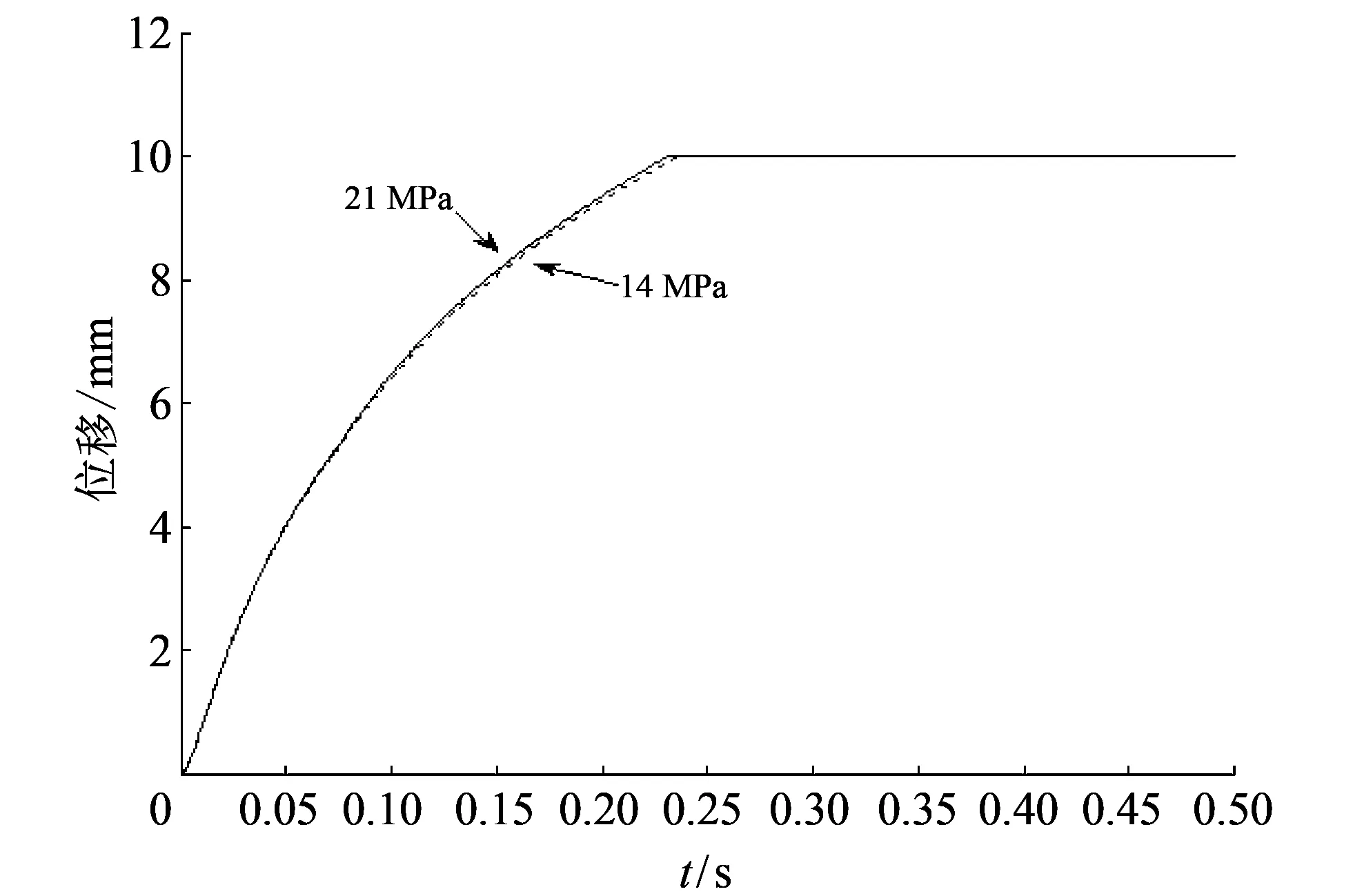
图 4　位置控制回路在鲁棒增益调度控制器下的阶跃响应Fig.4　Position control loop step response under robust gain scheduling

图 5 为位置控制回路在直接切换和模糊切换控制器下的位移输出.

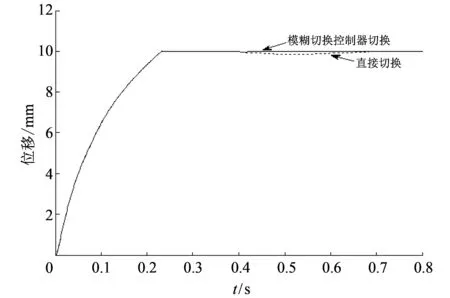
图 5　两种切换方式下的位移输出Fig.5　Position output under two switching mode

如图 5 所示， 泵源压力在0～0.4 s设定为 21 MPa， 在0.4～0.8 s设定为14 MPa， 则从位置控制回路位移输出中可以看出， 直接切换时位移输出会出现一定的抖动， 抖动幅值大约为0.2 mm， 而采用模糊切换控制器时则几乎没有这种现象. 这是因为直接切换时， 位置控制回路参数会有较大的变化， 而模糊切换控制器有效削弱了切换时产生的抖动， 实现了平滑切换. 但由于抖动无关消除， 故采用模糊切换控制时仍有轻微抖动， 但相比直接切换已大大减小.

5　结　论

本文针对泵阀联合EHA分级压力控制下位置控制回路性能改变的问题， 设计了控制器， 仿真结果表明：

1) 当泵源压力分别为14 MPa和21 MPa时， 位置控制回路响应速度分为为0.237s和0.239s， 两者响应速度基本一致， 说明本文所设计的控制器有效， 实现了位置控制回路在不同泵源压力下增益基本保持一致的功能.

2) 模糊切换控制器有效削弱了不同工作模式切换瞬间引起的抖动， 实现了平滑切换.

本文方法同样适用于类似的大范围工况和参数时变性的系统， 尤其是在航空、 航天等对控制精度要求较高的领域.