基于FCM-ANFIS模型的船舶交通流预测

惠子刚， 肖建兵

(青岛远洋船员职业学院 航海系，山东 青岛 266071)

成山头水域是我国重要的海洋渔场，同时也是各种船舶进出黄海和渤海的必经要道。该水域水文环境复杂，交通繁忙，交通流比较密集。此外，由于我国沿海南北航线上的船舶均在该水域汇集，因此该水域的航行环境比较复杂，易发生水上交通事故。据统计，该水域平均每年的船舶交通流量近20万艘。[1]随着船舶大型化的发展和船舶数量的日益增多，该水域的海上交通安全状况日益严峻。因此，对该水域内的船舶交通流进行准确预测具有重要意义。

1) 提前对该水域内的船舶交通流量进行准确预测，可为相关海事管理部门提供交通管制决策；在船舶交通流量较大时采取适当的交通管制措施，可在一定程度上缓解分道通航航道内的交通压力，提高船舶航行效率。

2) 进行交通流预测可为通航分道制的制订和规划提供参考[2]，在船舶比较密集的航行区域，分道通航制可在很大程度上规范船舶的航行行为，疏通和指导船舶交通流向，进而减小船舶因无规律航行而发生事故的概率。

3) 进行船舶交通流预测可为船舶驾驶人员提供航行预警信息，使其在船舶密集的水域根据相应的预测交通流量提前做好谨慎航行措施，并在设计航线时适当根据船舶交通流量的预测状况采取一定的措施避开船舶过多的水域。

因此，船舶交通流预测可为船舶计划航线设计及在复杂水域和交通流密集水域安全航行提供参考，从而减少船舶事故的发生。此外，船舶交通流预测可为港口建设、航道设计及船舶安全航行与管理提供可靠的支持和保障，使进出港口航道的可航能力得到充分发挥。当前，相关研究人员[3-5]已提出不同的模型和算法进行船舶交通流量分析预测。

随着人工神经网络技术的飞速发展及神经网络自学习和非线性映射能力的不断增强，人工神经网络技术在海洋工程及其他工程领域得到广泛应用。BP(Back Propagation)神经网络属于多层前馈神经网络，是应用最广泛的神经网络模型之一。BP神经网络及其各种优化的预测模型在船舶交通流预测领域和其他预测领域的应用也十分广泛。然而，传统的BP神经网络存在一些缺点[6]，即：BP网络训练参数的选择具有随机性；模型参数的确定敏感性较高，收敛速度相对比较难控制等。

模糊系统[7]是一种可有效处理非线性问题的工具，但其与人工神经网络之间的特性存在较大差异。前者适合表述模糊的或定性的理论[8]，但其自学习能力相对较差[9]。

为进一步提高预测精度，并综合考虑模糊系统和神经网络的优缺点，提出一种基于模糊C均聚类自适应神经模糊推理系统(Fuzzy C-Means Clustering Algorithm with Adaptive Neural-Fuzzy Inference System)的船舶交通流预报模型。该模型采用模糊C均值聚类算法获取模糊规则数量，并采用BP算法和最小二乘估计算法对模型参数进行训练学习。模型的输入变量采用相关分析法确定。最后选取成山头船舶自动识别系统(Automatic Identification System，AIS)基站的船舶交通流记录数据进行交通流预报仿真，试验结果表明本文提出的方法可有效实现交通流的准确预报。

1 自适应神经模糊推理系统

JANG[10]提出自适应神经模糊推理系统(Anlaptive Neural-Fuzzy Inference System, ANFIS)，该模型是一种基于Takagi-Sugeno模型的系统。ANFIS拥有模糊系统的决策判断能力和神经网络的自学习能力，在不同研究领域得到广泛应用。[11-12]典型的简单2条规则ANFIS结构为

IfxisA1andyisB1， thenf1=a1x+b1y+c1

IfxisA2andyisB2， thenf2=a2x+b2y+c2

(1)

式(1)中:A和B为与输入节点相关的模糊变量。对应的ANFIS结构见图1。

经典的ANFIS模型共由5层结构组成。

1) 第一层为数据模糊化层，包括ANFIS的前件可调模型参数。

2) 第二层为计算前件网络模糊集及模糊规则的适应度计算层。

3) 第三层为归一化计算第二层的输出。

4) 第四层为计算出每条规则的输出，包含ANFIS的后件可调模型参数。

5) 第五层为计算全部规则的输出和，即后件的输出值。

由模糊推理系统的输入与输出之间的关系及整个ANFIS模型的网络结构分析可知，该模型主要通过对采样数据进行训练学习，自适应地调整整个网络模型的网络参数(包括前件参数和后件参数)。为进一步提高网络模型的效率和精度，ANFIS模型采用结合BP算法与最小二乘算法的混合算法进行网络训练。采用BP算法调整模型的条件参数(前件参数)，采用线性最小二乘估计算法调整结论参数(后件参数)。该算法可减少模型的学习时间，提高模型搜索效率。模型的输出为

(2)

2 模糊C均值聚类(FCM)算法

模糊C均值聚类[13]算法通常采用隶属度函数确定采样点的隶属聚类中心。算法的核心是循环计算并修正属于隶属度函数的聚类中心和分类矩阵，从而完成聚类分类。FCM将n个数据矢量Xi(i=1,2,…,n)分解为C个模糊组，在满足衡量代价函数最小的条件下，计算各模糊组的聚类中心。FCM使用[0-1]之间的隶属度值确定采样数据的隶属度程度。通常通过数据的初始化处理，使一个采样数据组合的隶属度总和为1，即

(3)

FCM的代价函数通常表示为

(4)

3 预测模型建模

3.1 数据分析

相关性分析[14]源于时间序列和数据信号的处理，可定量显示出一组原始时间序列数据中任意2个不同时间序列数据之间的关系和这2个数据随时间变化的状况。自相关分析可定量描述时间序列任意相邻数据之间的关联性。自相关和偏自相关函数[15]通常可有效分析复杂时间序列问题：自相关函数可刻画时间序列相邻变量之间的关联性；偏相关函数可在剔除中间变量影响的基础上准确描述2个变量之间的关联性。船舶交通流时间序列受到诸多不确定性因素的影响，包括海上天气状况、海上交通密集程度和交通管制等。这些不确定要素具有较强的不确定性和非线性，一般难以精确计算出其对船舶交通流的影响。本文采用相关分析方法对海上船舶交通流时间序列值之间的关联性进行分析研究，确定所建预测网络模型输入变量的个数。选取0.3的相关值确定模型输入变量的个数，结果见图2。由图2可知：船舶交通流数据的自相关系数拖尾，且其自相关系数逐渐向零靠近并趋于稳定，说明船舶交通流数据的时间序列为平稳时间序列；船舶交通流数据的偏自相关系数5阶截尾。这表明t时刻与t-5至t-1时刻之间的船舶交通流时间序列数据存在较强的相关性，预测模型选取前5个连续时刻点作为输入变量。此次仿真试验选用成山头水域船舶交通管理系统(Vessel Traffic Service, VTS)岸基观测站2014年8月1日至2014年8月30日共30组数据进行仿真训练和预测，采用前60%的数据对模型进行训练学习，采用后40%的数据进行仿真验证。实测数据采样间隔为1 d。

3.2 预测建模

建立并采用基于FCM算法的ANFIS模型进行船舶交通流预测的步骤：

1) 对船舶交通流时间序列数据进行相关分析，

确定预测模型的输入变量个数为5，输出变量个数为1；生成模型的训练学习时间序列。

2) ANFIS预测模型采用前60%的数据进行系统仿真训练，采用后40%的数据进行仿真预测检验。

3) 采用FCM算法进行时间序列样本分析聚类，进而得到样本的聚类中心和个数，确定预测模型的模糊规则数。本文模糊C均值聚类算法的初始聚类中心数为15，最大迭代次数为200，分割矩阵指数为2，目标误差准则为0.000 01；ANFIS预测系统的迭代循环次数为200，初始步长为0.01，误差目标为0，步长递减率为0.8，步长增大率为1.5。

4) 采用BP算法和线性最小二乘估算法对预测模型的参数进行学习训练，若满足误差要求或达到迭代次数，则终止训练。

5) 得到最优的ANFIS模型，采用船舶交通流时间序列数据进行仿真预测。

6) 计算误差，得到最终的交通流预测值。

4 仿真结果与讨论

为比较所选预测模型的预测准确度，引入均方根误差(RMSE)、标准差(SD)和绝对误差(MAE)作为预测模型的预测结果评价标准，其计算式为

(5)

(6)

(7)

图3为利用4个不同的预测模型预测得到的船舶交通流预测值(BP, FCM-ANFIS及SC-ANFIS)。对应4种预测模型的4个不同的测量标准值(RMSE，MAE和SD)见表1。

该模型的预测结果与实测船舶交通流数量比较吻合。由表1可知，FCM-ANFIS模型的预测误差比几种传统的预报模型的误差小。仿真试验在一定程度上验证了本文所建模型在船舶交通流预测应用方面的适用性。这表明FCM-ANFIS模型可为船舶交通流预测提供一种精度更高的预测研究方向。船舶交通流量预测结果见表1和表2。

艘

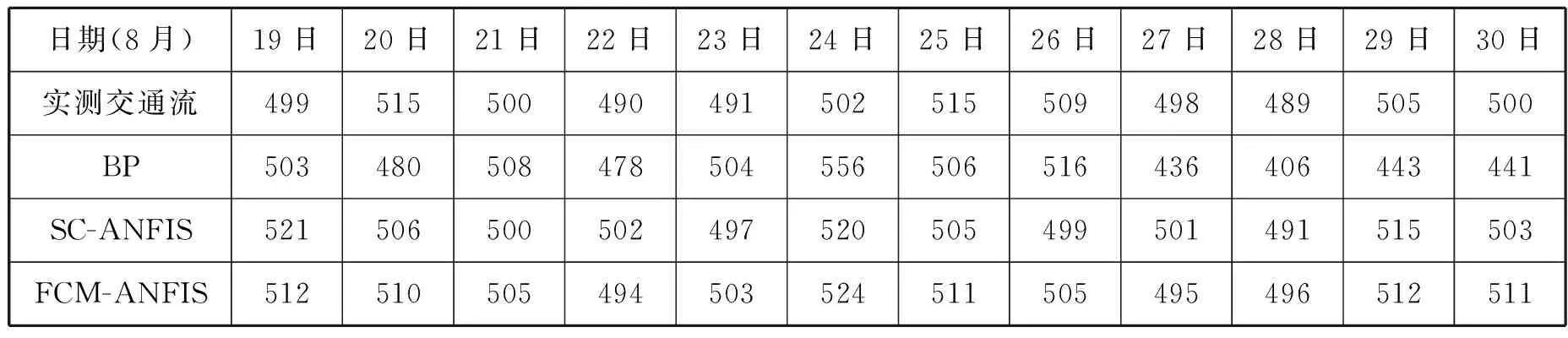
表2 预测结果对比 艘

5 结束语

对特定水域进行准确的船舶交通流预测可为船舶操纵人员提供通航环境和未来交通流量的参考依据，为船舶计划航线设计及在复杂水域和交通流密集水域安全航行提供参考，同时为海事管理部门提供决策参考，以便提前掌握船舶交通状况，提前管理安排，从而减少船舶事故的发生，保证海上安全。

本文提出一种基于模糊C均值聚类自适应神经模糊推理系统的模块化(FCM-ANFIS)中国沿海船舶交通流预测模型。采用相关分析法确定模型的输入变量,采用FCM算法确定聚类中心。预测模型采用BP算法和最小二乘算法进行网络参数训练，在一定程度上克服了传统模型收敛速度慢等问题。同时，选用基于AIS的船舶交通流数据进行仿真预报，仿真结果具有较高的预测精度。但是，模型的预测精度会随着预报时间的增加而有一定程度的下降，因此采用提出的模型进行长期船舶交通流预报并提高预报精度是后续需开展的主要研究工作。

[1] 林威. 基于AIS数据的船舶交通流特性统计平台研究[D]. 大连:大连海事大学, 2017.

[2] 颜江峰. 船舶定线制对提高通航效率的作用[J]. 船海工程, 2006, 35(4):83-84.

[3] 王东, 熊锡龙. 基于影响因素分析的船舶交通流量预测多元线性回归模型[J]. 船海工程, 2010, 39(3):178-180.

[4] 田燕华, 陈锦标. 基于BP神经网络的船舶交通流量预测研究[J]. 船海工程, 2010, 39(1):122-125.

[5] 李俊, 徐志京, 唐贝贝. 基于GA优化的灰色神经网络船舶交通流量预测方法研究[J]. 船海工程, 2013, 42(5):135-137.

[6] BASERI H, BAKHSKI-JOOYBARI M, RAHMANI B. Modeling of Spring-Back in V-Die Bending Process by Using Fuzzy Learning Back-Propagation Algorithm [J]. Expert Systems with Application, 2011, 38(7): 8894-8900.

[7] 从爽. 神经网络、模糊系统及其在运动控制中的应用[M]. 合肥: 中国科学技术大学出版社, 2001.

[8] 肖建，白裔峰，于龙. 模糊系统结构辨识综述[J]. 西南交通大学学报, 2006, 41(2): 135-142.

[9] 戴文战，娄海川，杨爱萍. 非线性系统神经网络预测控制研究进展[J].控制理论与应用, 2009, 26(5):521-530.

[10] JANG J S R. ANFIS: Adaptive-Network-Based Fuzzy Inference Systems [J]. IEEE Transactions on Systems Man and Cybernetics, 1993, 23(3):665-685.

[11] 康正亮, 胥凯晖, 杨传起. ANFIS在航材需求量预测中的应用[J]. 四川兵工学报,2015,36(1):84-87.

[12] 张凯铭. 基于ANFIS的区域汽车市场销售量预测研究[D]. 吉林: 吉林大学, 2011.

[13] BEZDEK J C. Cluster Validity with Fuzzy Sets [J]. Journal of Cybernetics, 1973, 3(3):58-73.

[14] 于宁莉, 易云东, 涂先勤. 时间序列中自相关与偏自相关函数分析[J]. 数学理论与应用, 2007, 27(1):54-57.

[15] 李立春. 自相关函数在时间序列分析中[J]. 上海统计, 2001(6):28-29.